DiscreteWaveletData
✖
DiscreteWaveletData
ウェーブレット指標 windi,ウェーブレット wave,ウェーブレット変換 wtrans に対応するウェーブレット係数 coefiを持つ離散ウェーブレットデータオブジェクトを与える.
詳細とオプション




- DiscreteWaveletData[{wind1->coef1,…},…]は常にDiscreteWaveletData[coefs,winds,…]という構造の最適化された標準形に変換される.
- 係数 coefiは任意の深さの配列,Image[…], Sound[…],SampledSoundList[…]オブジェクトのいずれでもでよい.
- ウェーブレット変換 wtrans で使われるオプションはDiscreteWaveletDataのオプションとしても使うことができる.
- 標準出力形式では,省略された wtrans,細分化の数,もとのデータの次元のみが出力される.
- Normal[DiscreteWaveletData[…]]は,ウェーブレット指標 windiと対応する係数配列 coefiの対応関係を示す規則のリスト{wind1->coef1,wind2->coef2,…}を与える.
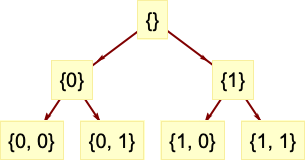
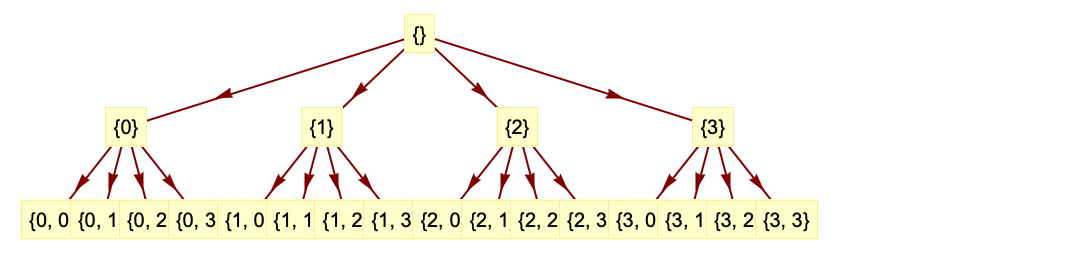
- DiscreteWaveletDataはウェーブレット分解木を表す.各ノードはウェーブレット係数を持つ.木の各ノードにはウェーブレット係数へのアクセスに使える一意的なウェーブレット指標ベクトルがある.
- ウェーブレット指標 wind は整数のベクトルである.ベクトルの長さはウェーブレット分解木における細分化のレベルを表す.長さ
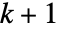 の指標ベクトルで,最初の
の指標ベクトルで,最初の 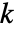 個の整数は親ノードを最後の整数は現行ノードと親ノードとの関係を示す.
個の整数は親ノードを最後の整数は現行ノードと親ノードとの関係を示す. - 一次元データでは,指標 wind は0と1からなる.0はローパスフィルタリングを表し,1はハイパスフィルタリングを表す.
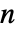 次元データの指標 wind は
次元データの指標 wind は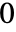 から
から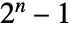 までの整数からなる.各整数はデータの各次元に沿って実行された操作のベクトルを表す.厳密な対応関係はMapThread[Rule,{Range[0,2^n-1],Tuples[{lowpass,highpass},n]}]で与えられる.
までの整数からなる.各整数はデータの各次元に沿って実行された操作のベクトルを表す.厳密な対応関係はMapThread[Rule,{Range[0,2^n-1],Tuples[{lowpass,highpass},n]}]で与えられる.- ウェーブレット指標 wind を使ってDiscreteWaveletDataオブジェクト dwd からウェーブレット係数を抽出することができる.以下は使用可能な指定値である.
-
dwd[wind] wind に対応する係数を抽出する dwd[{wind1,wind2,…}] いくつかのウェーブレット係数配列を抽出する dwd[wpatt] wind がパターン wpatt にマッチする係数すべてを抽出する dwd[All] すべての係数を抽出する dwd[Automatic] 逆変換で使用される係数を抽出する - デフォルトで,係数は規則のリスト{wind1->coef1,wind2->coef2,…}として返される.
- dwd[…,{form1,form2,…}]を使って出力形が制御できる.使用可能な formiは以下の通りである.
-
"Rules" 規則 {wind1->…} "Values" 係数のみ "Inverse" 個々の係数の逆変換 "ListPlot" 1D係数の単純なリストプロット "MatrixPlot" 2D係数の単純な行列プロット "Image" 画像係数のための画像 "Sound" サウンド係数のためのサウンドオブジェクト "SampledSoundList" サウンド係数のためのサンプルサウンドオブジェクト - 全体的な特性はDiscreteWaveletData[…]["prop"]で得られる.
- DiscreteWaveletData[…]["Properties"]はDiscreteWaveletDataオブジェクトで使用可能な特性のリストを与える.
- 変換係数の関連特性
-
"BasisIndex" 逆変換に使用するウェーブレット指標 "Dimensions" ウェーブレット係数群の次元を与える "EnergyFraction" 係数群におけるエネルギーの割合 "Padding" データ変換に使用する充填 "Refinement" 実行する細分化レベルの数 "Transform" ウェーブレット変換のタイプ {"TreeView",pos} TreePlotにおけるのと同じように pos を使った分解の木のビュー "Wavelet" 使用するウェーブレット族 "WaveletIndex" すべてのウェーブレット指標 windiのリスト - 入力データ関連特性
-
"DataDimensions" もとのデータの次元 "DataChannels" データのチャンネル数 "DataWrapper" 再構築の後でデータに適用されるラッパー関数 - パケット変換に特有な特性
-
"BestBasisBlockView" 最良基底のブロック格子ビュー "BestBasisCostValues" 各ウェーブレット係数の費用値 "BestBasisCostTable" フォーマットされた費用値表 - WaveletThresholdから得られる dwd の特性
-
"ThresholdValues" 各ウェーブレット係数の閾値 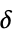
"ThresholdTable" フォーマットされた閾値 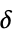
- 使用可能なオプション
-
Method Automatic 使用するメソッド Padding "Periodic" データを境界を越えてどのように延長するか SampleRate Automatic サウンドデータに使用するサンプルレート WorkingPrecision MachinePrecision 内部計算で使用する精度 - Paddingの設定値はArrayPadで使用できるものに等しい.
例題
すべて開くすべて閉じる例 (3)基本的な使用例
ウェーブレット変換からDiscreteWaveletDataを得る:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ngro3j
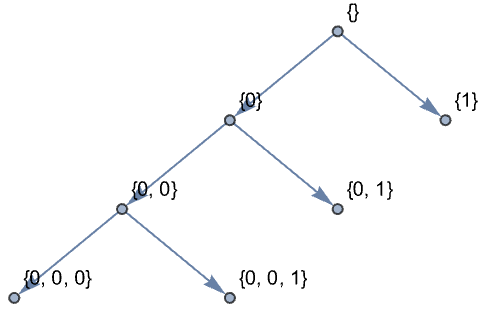
DiscreteWaveletDataは変換係数の木を表す:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-4k7wse
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ff5yaq
DiscreteWaveletDataオブジェクトを他のウェーブレット関数で使う:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-nmt8l0
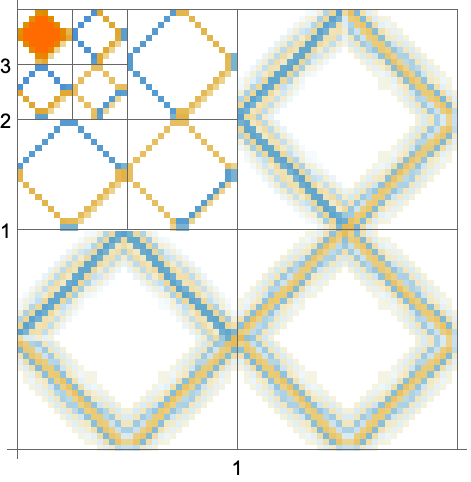
WaveletMatrixPlot[dwd]を使い,階層的な格子レイアウトウェーブレット係数の行列をプロットする:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-21l62m
静的ウェーブレット変換係数の逆ウェーブレット変換を計算する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-dktatf
スコープ (25)標準的な使用例のスコープの概要
基本的な用法 (8)
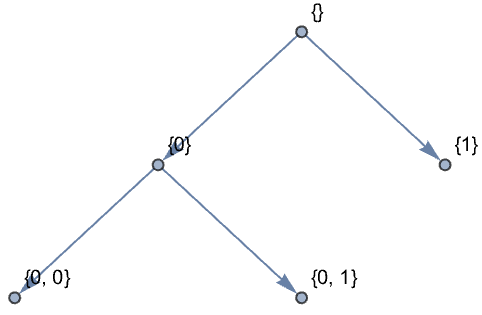
DiscreteWaveletTransformのようなウェーブレット変換からDiscreteWaveletDataを得る:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-dua9ap
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bstvmp
https://wolfram.com/xid/0ixfzxjfk8fh8n2-dwznbn
InverseWaveletTransformはDiscreteWaveletDataに対して使うことができる:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-3exuz
HaarWavelet[]のような直交ウェーブレットには逆変換は厳密値である:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-kbjry7
https://wolfram.com/xid/0ixfzxjfk8fh8n2-q1m6j
https://wolfram.com/xid/0ixfzxjfk8fh8n2-xstdo
{0,_}という形式のウェーブレット指標に対応する全係数を抽出する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-kdvwmd
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fi53sf
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bbagie
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ca22gi
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bhkppp
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bysrmy
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fcmoa

DiscreteWaveletDataを他のウェーブレット関数で使う:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-5ve1p
https://wolfram.com/xid/0ixfzxjfk8fh8n2-x0a1p
https://wolfram.com/xid/0ixfzxjfk8fh8n2-zw6ko
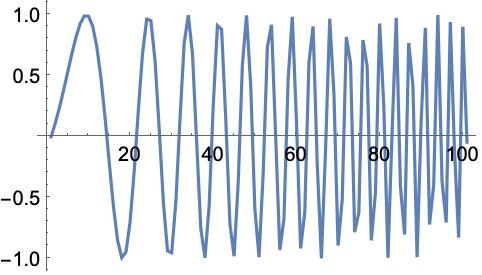
https://wolfram.com/xid/0ixfzxjfk8fh8n2-f7srhe
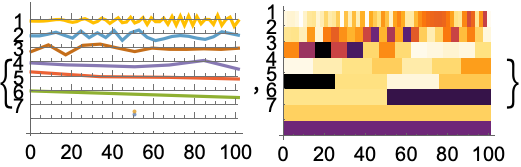
ウェーブレット関数を使ってDiscreteWaveletDataを変換する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ccpsk
https://wolfram.com/xid/0ixfzxjfk8fh8n2-in57yu
https://wolfram.com/xid/0ixfzxjfk8fh8n2-do6zrf
https://wolfram.com/xid/0ixfzxjfk8fh8n2-c0frxo
https://wolfram.com/xid/0ixfzxjfk8fh8n2-f31e44

係数配列を与える規則のリストからDiscreteWaveletDataを構築する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-d7j35v
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ei3p5y
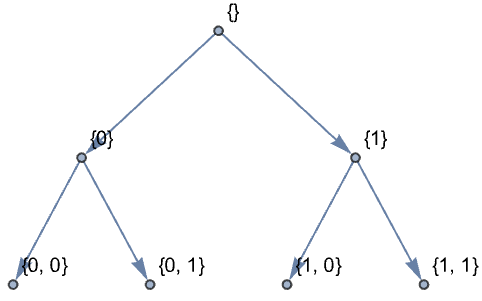
https://wolfram.com/xid/0ixfzxjfk8fh8n2-h2s7um
指定のウェーブレットと前方変換を使ってDiscreteWaveletDataを構築する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-islkuu
https://wolfram.com/xid/0ixfzxjfk8fh8n2-dgjcuc
係数を得る (7)
https://wolfram.com/xid/0ixfzxjfk8fh8n2-cz6cl3
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bzllae
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bd6bpg
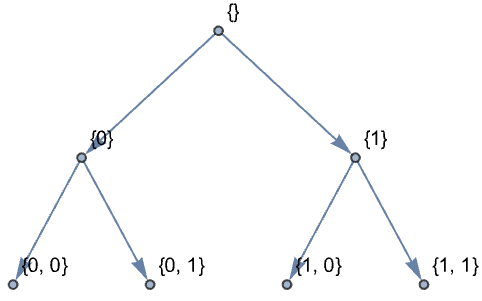
DiscreteWaveletDataから係数配列を抽出する異なるウェーブレット指標指定:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-iy60ll
https://wolfram.com/xid/0ixfzxjfk8fh8n2-or3m
https://wolfram.com/xid/0ixfzxjfk8fh8n2-dqfk06
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fcyaju
https://wolfram.com/xid/0ixfzxjfk8fh8n2-lqfcxp
https://wolfram.com/xid/0ixfzxjfk8fh8n2-k8olxz
https://wolfram.com/xid/0ixfzxjfk8fh8n2-mi1wc
https://wolfram.com/xid/0ixfzxjfk8fh8n2-f4cpy
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ctsim
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fr7p9t
https://wolfram.com/xid/0ixfzxjfk8fh8n2-10jyz
https://wolfram.com/xid/0ixfzxjfk8fh8n2-d3i65f
https://wolfram.com/xid/0ixfzxjfk8fh8n2-idete0
https://wolfram.com/xid/0ixfzxjfk8fh8n2-b120x3
https://wolfram.com/xid/0ixfzxjfk8fh8n2-j1pbm5
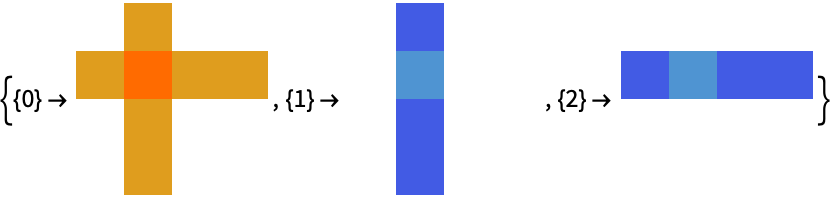
https://wolfram.com/xid/0ixfzxjfk8fh8n2-b3el86
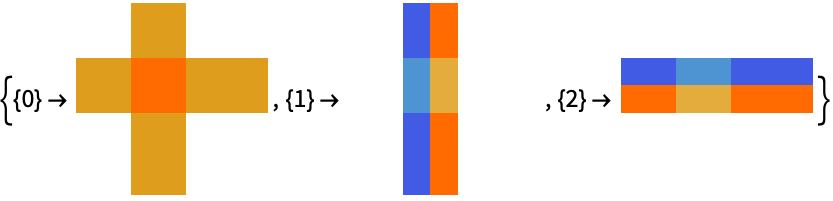
画像ウェーブレット係数をデフォルトでImageAdjustが適用されたImageオブジェクトとして得る:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-xndhf
https://wolfram.com/xid/0ixfzxjfk8fh8n2-d0ftd
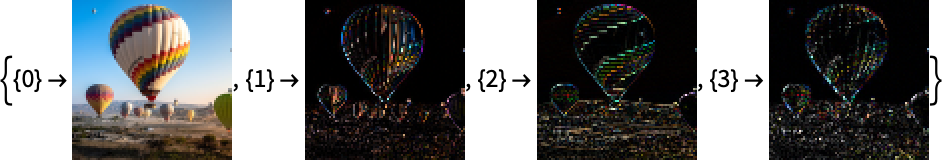
https://wolfram.com/xid/0ixfzxjfk8fh8n2-b7r9gb
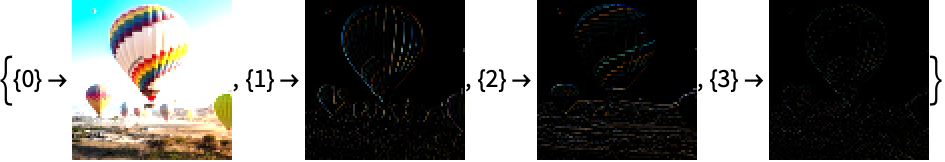
デフォルトで,画像ウェーブレット係数は各カラーチャンネルの画素値の配列として与えられる:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bf8m16
https://wolfram.com/xid/0ixfzxjfk8fh8n2-vw4rx
音声ウェーブレット係数をAudioオブジェクトとして得る:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-b42v8
https://wolfram.com/xid/0ixfzxjfk8fh8n2-nseizy
個々の係数のAudioオブジェクトとしての逆変換:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-b815mo

サウンドウェーブレット係数をSoundオブジェクトとして得る:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-c5i7eb
https://wolfram.com/xid/0ixfzxjfk8fh8n2-efuxli
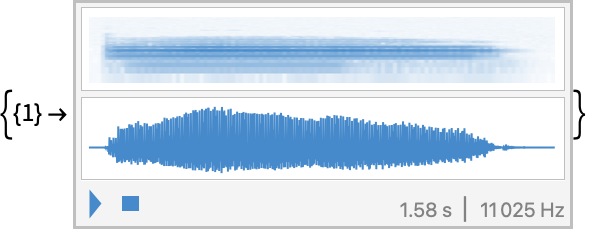
Soundオブジェクトとしての個々の係数の逆変換:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-lrlgkr
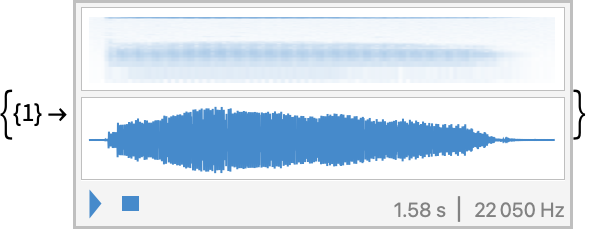
係数を設定する (6)
List入力のためにDiscreteWaveletDataを構築する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ucud2p
https://wolfram.com/xid/0ixfzxjfk8fh8n2-1v1oqv
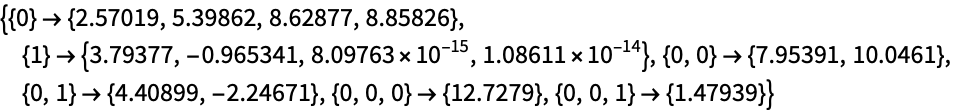
List係数には,タイプが{wind1->coef1,…}の規則 wrules のリストを入力する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-lwd6yz
https://wolfram.com/xid/0ixfzxjfk8fh8n2-nv7202
Image入力:

https://wolfram.com/xid/0ixfzxjfk8fh8n2-gzwu9f
https://wolfram.com/xid/0ixfzxjfk8fh8n2-if2b33
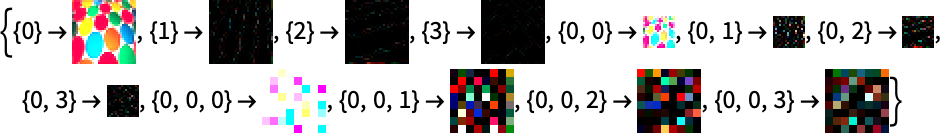
Image係数には,タイプ{wind1->icoef1,…}の規則 irules のリストを入力する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-foqhyb
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ocw19v

Sound入力:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-03dvgu
https://wolfram.com/xid/0ixfzxjfk8fh8n2-jod9ca
https://wolfram.com/xid/0ixfzxjfk8fh8n2-gevv9q
Sound係数には,タイプ{wind1->scoef1,…}の規則 srules のリストを入力する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ht6sq4
https://wolfram.com/xid/0ixfzxjfk8fh8n2-tdousc
デフォルトで,パラメータウェーブレット変換 wtrans は自動的に計算される:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ttyarm
https://wolfram.com/xid/0ixfzxjfk8fh8n2-29z9g1
https://wolfram.com/xid/0ixfzxjfk8fh8n2-uwz1vm
https://wolfram.com/xid/0ixfzxjfk8fh8n2-0q1566
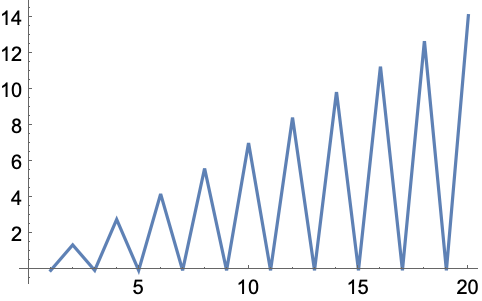
デフォルトで,データの次元 {d1,…}は自動的に計算される:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-l6et16
https://wolfram.com/xid/0ixfzxjfk8fh8n2-pxabo7
https://wolfram.com/xid/0ixfzxjfk8fh8n2-tqpdgp
https://wolfram.com/xid/0ixfzxjfk8fh8n2-new4jb
https://wolfram.com/xid/0ixfzxjfk8fh8n2-2i5y6u

特性 (4)
https://wolfram.com/xid/0ixfzxjfk8fh8n2-cwo7hg
https://wolfram.com/xid/0ixfzxjfk8fh8n2-dvucjy
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ew4hlg
https://wolfram.com/xid/0ixfzxjfk8fh8n2-h530x2
https://wolfram.com/xid/0ixfzxjfk8fh8n2-hm2to2
https://wolfram.com/xid/0ixfzxjfk8fh8n2-4gkxs

https://wolfram.com/xid/0ixfzxjfk8fh8n2-krkjr9
https://wolfram.com/xid/0ixfzxjfk8fh8n2-b2qkf8
https://wolfram.com/xid/0ixfzxjfk8fh8n2-eb5099
全係数の木あるいはブロック格子でハイライトされたウェーブレット基底を示す:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-g69er
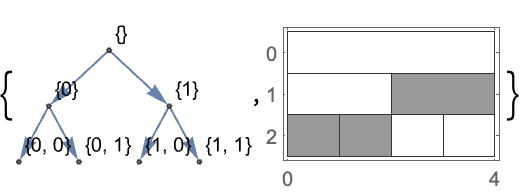
https://wolfram.com/xid/0ixfzxjfk8fh8n2-eivna
WaveletBestBasisで計算された基底の各係数配列の費用値:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ekgh6q

https://wolfram.com/xid/0ixfzxjfk8fh8n2-g77h01
https://wolfram.com/xid/0ixfzxjfk8fh8n2-btkqm6
https://wolfram.com/xid/0ixfzxjfk8fh8n2-2b963
https://wolfram.com/xid/0ixfzxjfk8fh8n2-e509ba
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ko26av
オプション (7)各オプションの一般的な値と機能
Method (1)
Methodの設定値はウェーブレット変換のメソッドと同じである:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-tc1lp2
DiscreteWaveletDataを生成して"IntegerLifting"を行う:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-sk3nxr
https://wolfram.com/xid/0ixfzxjfk8fh8n2-yt6n1g
Padding (2)
Paddingの設定値は"Periodic"を含むArrayPadのメソッドと同じである:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-dehf7e
https://wolfram.com/xid/0ixfzxjfk8fh8n2-qpkfr
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ldsb8a
https://wolfram.com/xid/0ixfzxjfk8fh8n2-sme52
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ntyqgp
https://wolfram.com/xid/0ixfzxjfk8fh8n2-pojqqw
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bsohej
デフォルトで,Padding->"Periodic"オプションが使われる:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-5tzzf7
SampleRate (1)
Sound入力には,SampleRateが自動的に計算される:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-xc74fv
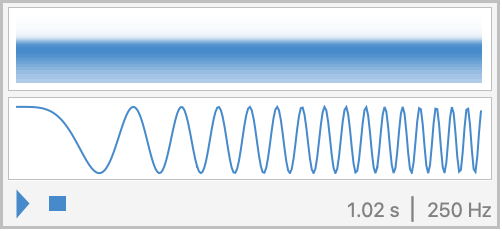
https://wolfram.com/xid/0ixfzxjfk8fh8n2-u0mal1
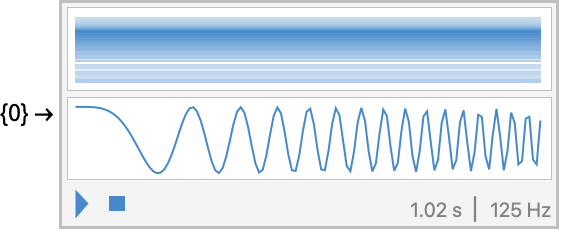
デフォルトで,SampleRateが最初の係数規則から抽出される:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-vh5x4x
https://wolfram.com/xid/0ixfzxjfk8fh8n2-45juhj
https://wolfram.com/xid/0ixfzxjfk8fh8n2-8fcs5p
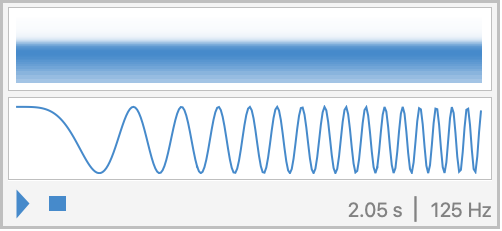
SampleRateを明示的に指定する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-5n0c5k
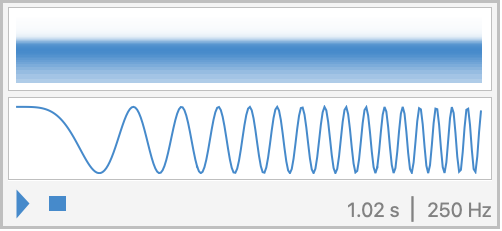
WorkingPrecision (3)
デフォルトで,WorkingPrecision->MachinePrecisionが使われる:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fvcmsi
https://wolfram.com/xid/0ixfzxjfk8fh8n2-qlff3u
https://wolfram.com/xid/0ixfzxjfk8fh8n2-7qfsoe
https://wolfram.com/xid/0ixfzxjfk8fh8n2-6lkrhl
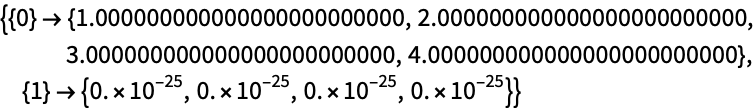
https://wolfram.com/xid/0ixfzxjfk8fh8n2-cqyqyd
厳密計算にWorkingPrecision->∞ を使う:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-m5fvtb
https://wolfram.com/xid/0ixfzxjfk8fh8n2-n6h6y1
https://wolfram.com/xid/0ixfzxjfk8fh8n2-5ais8y
https://wolfram.com/xid/0ixfzxjfk8fh8n2-136mk3
https://wolfram.com/xid/0ixfzxjfk8fh8n2-4vdn92
アプリケーション (3)この関数で解くことのできる問題の例
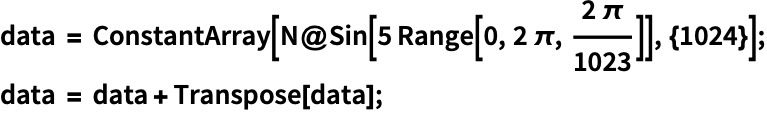
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fznl6r
https://wolfram.com/xid/0ixfzxjfk8fh8n2-oaq5i3
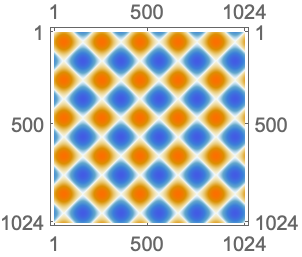
https://wolfram.com/xid/0ixfzxjfk8fh8n2-xhbvpg
https://wolfram.com/xid/0ixfzxjfk8fh8n2-frfgdg
data のByteCountと対応するウェーブレット係数 wcoeff を比較する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-453i24

https://wolfram.com/xid/0ixfzxjfk8fh8n2-1b2n8y
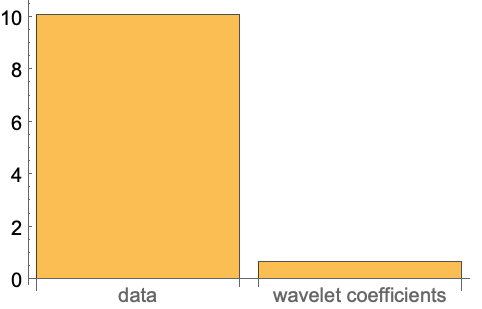
https://wolfram.com/xid/0ixfzxjfk8fh8n2-0kxmv7
https://wolfram.com/xid/0ixfzxjfk8fh8n2-c14zq1
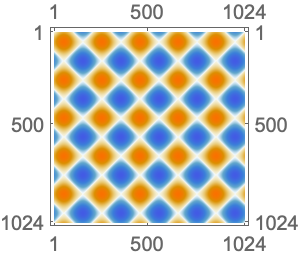
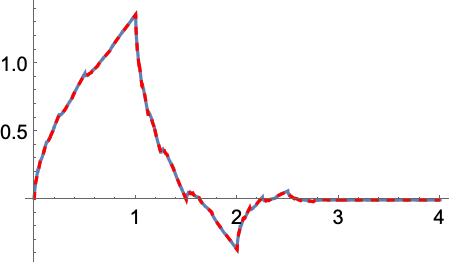
UnitVectorを詳細化レベル ![]() でローパス係数として設定してスケーリング関数
でローパス係数として設定してスケーリング関数 ![]() を計算する:
を計算する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-5rxdzs

https://wolfram.com/xid/0ixfzxjfk8fh8n2-8l0fx3
https://wolfram.com/xid/0ixfzxjfk8fh8n2-4dktqq

https://wolfram.com/xid/0ixfzxjfk8fh8n2-hh9jci
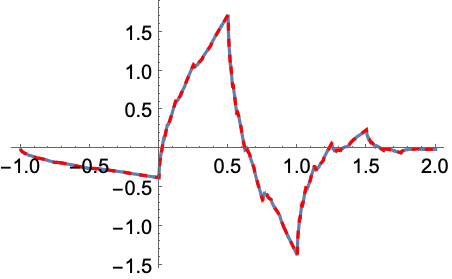
UnitVectorを詳細化レベル ![]() でハイパス係数として設定してウェーブレット関数
でハイパス係数として設定してウェーブレット関数 ![]() を計算する:
を計算する:

https://wolfram.com/xid/0ixfzxjfk8fh8n2-632mbc

https://wolfram.com/xid/0ixfzxjfk8fh8n2-7nkgui
https://wolfram.com/xid/0ixfzxjfk8fh8n2-kiybdg

https://wolfram.com/xid/0ixfzxjfk8fh8n2-n584i0
特性と関係 (4)この関数の特性および他の関数との関係
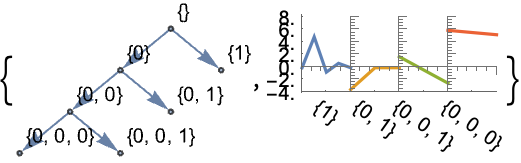
DiscreteWaveletDataは離散変換係数の木を表す:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-zzvt6
https://wolfram.com/xid/0ixfzxjfk8fh8n2-jalso3
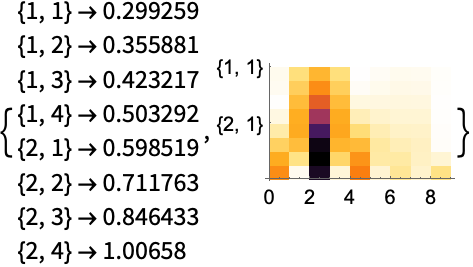
ContinuousWaveletDataはスケール集合における連続変換係数を表す:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fpkibb
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ohmn9
DiscreteWaveletDataをその係数と特性から再構築する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bfsdx
係数,ウェーブレット,使用する前方変換,データの次元を指定する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-gd9q04
https://wolfram.com/xid/0ixfzxjfk8fh8n2-dbr8jk
https://wolfram.com/xid/0ixfzxjfk8fh8n2-e5dvb8
https://wolfram.com/xid/0ixfzxjfk8fh8n2-gja6x7
Normalを使う:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-kygfk
すべて(All)の係数を明示的に抽出する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-e6kezw
任意のウェーブレット指標にマッチするパターンBlank[] (_)を指定する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-bhh5s
ウェーブレット指標指定に対応する係数配列のみを得る同等の方法:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-i1xfk7
dwd[wind]が返した各規則にLastを適用する:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-by6nzu
Partを使う:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fbkorx
https://wolfram.com/xid/0ixfzxjfk8fh8n2-fgn9vv
考えられる問題 (2)よく起る問題と予期しない動作
最良基底の費用値はWaveletBestBasisを使ってDiscreteWaveletDataについてのみ得ることができる:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ezwkcn
https://wolfram.com/xid/0ixfzxjfk8fh8n2-hmpbw
https://wolfram.com/xid/0ixfzxjfk8fh8n2-j3klm6
https://wolfram.com/xid/0ixfzxjfk8fh8n2-j6s02w

https://wolfram.com/xid/0ixfzxjfk8fh8n2-7f83z
DiscreteWaveletDataは仮定のために1つの矛盾しない前方変換を選ぶ:
https://wolfram.com/xid/0ixfzxjfk8fh8n2-ebaefq
https://wolfram.com/xid/0ixfzxjfk8fh8n2-eb6rn9
https://wolfram.com/xid/0ixfzxjfk8fh8n2-c73v2q
Wolfram Research (2010), DiscreteWaveletData, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.テキスト
Wolfram Research (2010), DiscreteWaveletData, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.
Wolfram Research (2010), DiscreteWaveletData, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.CMS
Wolfram Language. 2010. "DiscreteWaveletData." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.
Wolfram Language. 2010. "DiscreteWaveletData." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteWaveletData.html.APA
Wolfram Language. (2010). DiscreteWaveletData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteWaveletData.html
Wolfram Language. (2010). DiscreteWaveletData. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteWaveletData.htmlBibTeX
@misc{reference.wolfram_2025_discretewaveletdata, author="Wolfram Research", title="{DiscreteWaveletData}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteWaveletData.html}", note=[Accessed: 05-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_discretewaveletdata, organization={Wolfram Research}, title={DiscreteWaveletData}, year={2010}, url={https://reference.wolfram.com/language/ref/DiscreteWaveletData.html}, note=[Accessed: 05-April-2025
]}