ErlangDistribution
ErlangDistribution[k,λ]
形状母数 k,比率 λ のアーラン(Erlang)分布を表す.
詳細
- アーラン分布における値
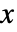 の確率密度は,
の確率密度は,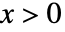 では
では 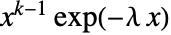 に比例し
に比例し 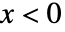 では0である.
では0である. - ErlangDistribution[k,λ]は各 xiがExponentialDistribution[λ]に従う,TransformedDistribution[x1+…+xk,…]に等しい.
- ErlangDistributionでは,k は任意の正の整数でよく,λ は任意の正の実数でよい.
- ErlangDistributionでは,λ は任意の単位次元の数量でよく,k は無次元量でよい. »
- ErlangDistributionは,Mean,CDF,RandomVariate等の関数とともに用いることができる.
予備知識
- ErlangDistribution[k,λ]は,2つの値 k と λ によってパラメータ化された区間
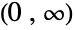 上の連続統計分布を表す.この分布は,独立同分布に従う (それぞれがXiExponentialDistribution[λ]の分布に従う)k 個の確率変数
上の連続統計分布を表す.この分布は,独立同分布に従う (それぞれがXiExponentialDistribution[λ]の分布に従う)k 個の確率変数  の和
の和  の分布として定義される.ここで,k は正の整数であり,λ は関連する確率密度関数(PDF)の全体的な高さ/傾きを決定する実数値の「サービス率」である.アーラン分布のPDFは連続で単峰性か単調減少で,領域の下限境界に近付く潜在的な不連続性がある.これに加え,PDFの裾部は,PDFが
の分布として定義される.ここで,k は正の整数であり,λ は関連する確率密度関数(PDF)の全体的な高さ/傾きを決定する実数値の「サービス率」である.アーラン分布のPDFは連続で単峰性か単調減少で,領域の下限境界に近付く潜在的な不連続性がある.これに加え,PDFの裾部は,PDFが 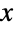 の大きい値について指数的にではなく代数的に減少するという意味で「厚い」(この動作は,分布のSurvivalFunctionを分析することで数量的に正確にできる).
の大きい値について指数的にではなく代数的に減少するという意味で「厚い」(この動作は,分布のSurvivalFunctionを分析することで数量的に正確にできる). - アーラン分布は,デンマーク人の数学者かつ統計学者であるAgner Krarup Erlangによって,1900年代の初めに電話回数の頻度のモデル化のために提案された.続く数年でアーラン分布は,待ち行列理論,特に系の現在の状態を与えた場合の待ち行列の条件付き待ち時間のモデル化で定期的に利用されるツールとなった.例えば,すでに3人が並んでいる待ち行列に並んだ場合に,期待される待ち時間
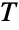 は TErlangDistribution[3,λ]を満足する.ただし,λ は1人あたりの平均応対時間の逆数である.
は TErlangDistribution[3,λ]を満足する.ただし,λ は1人あたりの平均応対時間の逆数である. - RandomVariateを使ってアーラン分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,ErlangDistribution[k,λ]](より簡略すると xErlangDistribution[k,λ])を使って,確率変数 x が,アーラン分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[ErlangDistribution[k,λ],x]およびCDF[ErlangDistribution[k,λ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がアーラン分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックアーラン分布を推定することが,FindDistributionParametersを使ってデータをアーラン分布にフィットすることができる.ProbabilityPlotを使って記号アーラン分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号アーラン分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたアーラン分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってアーラン分布を含む高次元分布を構築することが,ProductDistributionを使ってアーラン分布を含む独立成分分布の結合分布を計算することができる.
- アーラン分布は,(その定義を通して)指数分布を含む他の多くの分布と関連している.ErlangDistributionは, GammaDistribution[k, 1/λ]とPearsonDistribution[3, 1,(-k + 1)/λ, 0, 1/λ, 0]のPDFが両方ともErlangDistribution[k,λ]のPDFと厳密に等しいという意味で,GammaDistributionとPearsonDistributionの両方の特殊ケースでもある.k がInfinityに近付くにつれてErlangDistribution[k,λ]はNormalDistribution[k/λ,
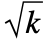 /λ]に収束し,ParetoDistributionはExponentialDistributionおよびErlangDistributionの商として得ることができる.さらに,ErlangDistributionは変換されたChiSquareDistributionに関連しており,ここから,NormalDistribution,LogNormalDistribution,RayleighDistribution,WeibullDistribution,MaxwellDistributionとの関係を継承している.
/λ]に収束し,ParetoDistributionはExponentialDistributionおよびErlangDistributionの商として得ることができる.さらに,ErlangDistributionは変換されたChiSquareDistributionに関連しており,ここから,NormalDistribution,LogNormalDistribution,RayleighDistribution,WeibullDistribution,MaxwellDistributionとの関係を継承している.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
k が大きくなると,尖度はNormalDistributionの尖度に近付く:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (5)
交通信号による遅れは平均0.5分で指数分布に従うと仮定する.ドライバーが同期されていない7つの信号がある道路を通るとし,すべての信号を通過する場合の遅れの分布を求める:
電話の通話時間は指数分布に従っていると仮定する.平均通話時間は3.7分である.連続する9回の通話時間が25分よりも長くなる確率を求める:
論理素子の遅延は指数分布に従い平均の遅延は![]() 秒であると仮定する.組合せ論理回路内で最長の論理素子のシーケンスが6個であるとして,6個すべての素子を通過する際の遅延が
秒であると仮定する.組合せ論理回路内で最長の論理素子のシーケンスが6個であるとして,6個すべての素子を通過する際の遅延が![]() 秒より長くなる確率を求める:
秒より長くなる確率を求める:
寿命にA,B,Cの3段階があるデバイスがある.各段階における時間は平均を10時間とする指数分布に従う.段階Cを過ぎるとデバイスは故障する.このデバイスの故障までの時間の分布を求める:
このようなデバイスが少なくとも40時間使用に耐える確率を求める:
独立した30個のデバイスの故障までの時間のシミュレーションを行う:
10個のデバイスで始まるシステムがある.デバイスのうち1個だけがアクティブで残りの9個は待機状態である.各デバイスの寿命は母数 ![]() でExponentialDistributionに従う.待機中のデバイスがある限り,1つのデバイスが故障するとすぐに別のデバイスに切り換えられる.この場合,このシステムの寿命は次の分布に従う:
でExponentialDistributionに従う.待機中のデバイスがある限り,1つのデバイスが故障するとすぐに別のデバイスに切り換えられる.この場合,このシステムの寿命は次の分布に従う:
特性と関係 (9)
アーラン分布は正の因子によるスケーリングの下では閉じている:
ErlangDistribution[k,λ]は k->∞で正規分布に収束する:
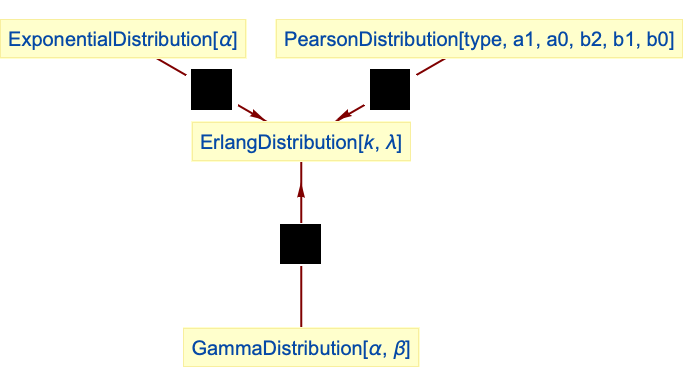
ExponentialDistributionに従っている k 個の変数の総和はアーラン分布に従う:
アーラン分布はタイプ3のピアソン分布(PearsonDistribution)の特殊ケースである:
アーラン分布はGammaDistributionの特殊ケースである:
ParetoDistributionはExponentialDistributionとErlangDistributionの商から求められる:
ParetoDistributionはErlangDistributionの商として求めることができる:
テキスト
Wolfram Research (2010), ErlangDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/ErlangDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "ErlangDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/ErlangDistribution.html.
APA
Wolfram Language. (2010). ErlangDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ErlangDistribution.html