FunctionMeromorphic
FunctionMeromorphic[f,x]
检验 ![]() 是否是 x 的一个亚纯函数.
是否是 x 的一个亚纯函数.
FunctionMeromorphic[f,{x1,x2,…}]
检验 ![]() 是否是 x1,x2,… 的一个亚纯函数.
是否是 x1,x2,… 的一个亚纯函数.
FunctionMeromorphic[{f1,f2,…},{x1,x2,…}]
检验 ![]() 是否是 x1,x2,… 的亚纯函数.
是否是 x1,x2,… 的亚纯函数.
FunctionMeromorphic[{funs,cons},xvars]
检验 ![]() 在一个包含约束条件 cons 的解的开集中是否是 xvars 的亚纯函数.
在一个包含约束条件 cons 的解的开集中是否是 xvars 的亚纯函数.
更多信息和选项

- 如果一个函数
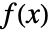 可以被表达成
可以被表达成 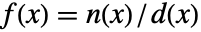 的形式,则该函数是亚纯函数,其中
的形式,则该函数是亚纯函数,其中 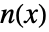 和
和 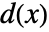 是复解析函数.
是复解析函数. - 如果一个函数
 可以被表达成
可以被表达成 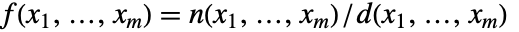 的形式,则该函数是亚纯函数,其中
的形式,则该函数是亚纯函数,其中  和
和  是复解析函数.
是复解析函数. - 如果 funs 包含除 xvars 以外的参数,则结果通常会是一个 ConditionalExpression.
- cons 可以包括不等式或它们的逻辑组.
- 可以给出以下选项:
-
Assumptions $Assumptions 参数的假设 GenerateConditions True 是否对参数生成条件 PerformanceGoal $PerformanceGoal 优先速度或优先质量 - GenerateConditions 的可能设置包括:
-
Automatic 只有非泛型条件 True 所有条件 False 没有条件 None 如果需要条件则返回未计算结果 - PerformanceGoal 的可能设置是 "Speed" 和 "Quality".
范例
打开所有单元关闭所有单元选项 (4)
Assumptions (1)
FunctionMeromorphic 不能为任意值的参数 ![]() 算出答案:
算出答案:
若假设 ![]() 是一个正整数,则 FunctionMeromorphic 可以成功:
是一个正整数,则 FunctionMeromorphic 可以成功:
GenerateConditions (2)
默认情况下,FunctionMeromorphic 可能对符号参数生成条件:
当 GenerateConditions->None 时,FunctionMeromorphic 不会给出一个有条件的结果,而是会失败:
设定 GenerateConditions->Automatic,则一般为真的条件不会被报告:
PerformanceGoal (1)
使用 PerformanceGoal 可避免可能出现的复杂计算:
应用 (12)
亚纯函数的分类 (7)
在一个平面内可视化这些函数,可以看出它们的奇点至少会是极点:
有分支切割的函数比如 Log 不是亚纯函数:
Sqrt 或任何带有非整数幂的函数也不是:
反三角函数和双曲线函数如 ArcSin、ArcTan 和 ArcCsch 同样也不是亚纯函数:
哪些只在实数输入上有定义的函数,比如 UnitStep 和 TriangleWave,也不会是亚纯函数:
由于所有三角函数和双曲线函数都是 Exp 的算数组合形式,它们都是亚纯函数:
可视化 Exp 和八个非解析型的三角函数和双曲线函数:
一个亚纯函数的奇点必须在复合情况下聚在一起,这样就会有一个非极点的奇点:
不像单变量函数一样,奇点在曲线上,在第一个函数中,是在 ![]() 曲线上:
曲线上:
完全 Beta 函数 ![]() 是亚纯函数:
是亚纯函数:
它可以被看做是一个多变量有理 Gamma 函数:
函数积分 (5)
亚纯函数的 Limit 要么是一个数字,要么是 ComplexInfinity:
Sqrt 有极限不存在的点,所以该函数不是亚纯函数:
亚纯函数的奇点,称为极点,有一个与之关联的 Residue:
沿着闭合等值线的亚纯函数的积分等于 ![]() 乘以曲线中极点留数之和. 计算原点旁
乘以曲线中极点留数之和. 计算原点旁 ![]() 的积分,这显然是其仅有的极点:
的积分,这显然是其仅有的极点:
如果一个函数的所有奇点都有相等的或相关的留数,则在闭合等值线上的积分可用于清点包围住的极点数量. 比如,![]() 在每一个
在每一个 ![]() 的半整数倍数位置上都有一个留数为
的半整数倍数位置上都有一个留数为 ![]() 的极点:
的极点:
![]() 在一个横跨实数轴的矩形上的积分可以对内含的半整数倍数
在一个横跨实数轴的矩形上的积分可以对内含的半整数倍数 ![]() 的个数进行计数:
的个数进行计数:
围道积分的一个常见应用是在实数线上计算积分,方法是通过将等值线扩展成一个在上半平面或下半平面是一个半圆的封闭区域。如果在半圆上方的积分部分消失,则围道积分必须等于实数积分。比如 ![]() . 该被积函数是亚纯函数:
. 该被积函数是亚纯函数:
对于有 ![]() 形式为
形式为 ![]() 的被积函数来说,
的被积函数来说,![]() 为亚纯函数,
为亚纯函数,![]() 在
在 ![]() 上连续,且对于大的
上连续,且对于大的 ![]() 而言,
而言,![]() ,积分
,积分 ![]() 可被计算成
可被计算成 ![]() 乘以上半平面中
乘以上半平面中 ![]() 的留数和. 使用这个方法计算
的留数和. 使用这个方法计算 ![]() . 首先,验证
. 首先,验证 ![]() 是亚纯函数:
是亚纯函数:
属性和关系 (5)
使用 D 计算导数:
使用 Series 计算泰勒级数的初始项:
使用 Solve 在单位圆盘中寻找 ![]() 的零点:
的零点:
使用 FunctionSingularities 在单位圆盘中寻找 ![]() 的极点:
的极点:
辐角原理说,![]() 的零点的个数和极点个数的差值可用
的零点的个数和极点个数的差值可用 ![]() 给出. 使用 NIntegrate 可以计算
给出. 使用 NIntegrate 可以计算 ![]() :
:
使用 Limit 验证所有 ![]() 都是
都是 ![]() 的极点:
的极点:
使用 FunctionAnalytic 检验 ![]() 和
和 ![]() 是否为解析函数:
是否为解析函数:
使用 FunctionSingularities 可求得所有奇点满足的条件:
使用 SolveValues 求奇点:
使用 FunctionPoles 求奇点及其多重性:
使用 ResidueSum 计算右半平面中的残差总和:
文本
Wolfram Research (2020),FunctionMeromorphic,Wolfram 语言函数,https://reference.wolfram.com/language/ref/FunctionMeromorphic.html.
CMS
Wolfram 语言. 2020. "FunctionMeromorphic." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionMeromorphic.html.
APA
Wolfram 语言. (2020). FunctionMeromorphic. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FunctionMeromorphic.html 年