GompertzMakehamDistribution

GompertzMakehamDistribution[λ,ξ]

尺度母数 λ，脆弱性の母数が ξ のGompertz分布を表す．

GompertzMakehamDistribution[λ,ξ,θ,α]

母数が λ，ξ，θ，α のGompertz–Makeham分布を表す．

詳細

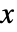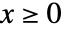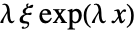  • Gompertz分布における値 のハザード関数は のときは で与えられ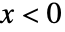，のときは0である．
  • Gompertz–Makeham分布における値 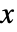のハザード関数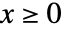は，のときは 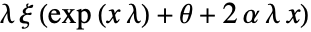で与えられ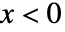，のときは0である．
  • GompertzMakehamDistributionでは，λ と ξ は任意の正の実数でよく，θ と α は任意の非負の実数でよい．
  • GompertzMakehamDistributionでは，λ は任意の単位次元の数量でよく，ξ，θ，α は無次元量でよい． »
  • GompertzMakehamDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる．

予備知識

  • GompertzMakehamDistribution[λ,ξ,θ,α]は，区間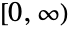上で定義され，2つの非負の実数 θ および α と，それぞれ「尺度母数」および「脆弱性母数」と呼ばれる2つの正の実数 λ および ξ によってパラメータ化された連続統計分布を表す．Gompertz–Makeham分布の確率密度関数(PDF)の全体的な動作は，母数 λ，ξ，θ，α の値によって決定される．特に，PDFは潜在的な特異点が領域の下限に近付く単調減少か単峰性である．さらに，母数によって，PDFの裾部は，PDFが 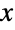の大きい値について代数的に減少するか指数的に減少するかによって，「太い」か「細い」のいずれかになる（この動作は分布のSurvivalFunctionを分析することで数量的に正確にできる）．この分布の2母数バージョンのGompertzMakehamDistribution[λ,ξ]は，しばしばGompertz分布と呼ばれ，GompertzMakehamDistribution[λ,ξ,0,0]に等しい．
  • Gompertz–Makeham分布は，英国人の数学者であるBenjamin Gompertzが1820年代初頭に研究した分布を，英国人の数学者であるW. M. Makehamが1890年代に一般化したことによって導入された．Gompertzによる当初の分布は人間の寿命をなめらかにモデル化するために構築されたもので，死が老化のみによってもたらされるという仮定によっているのに対し，Makehamの業績は，老化とその他のさまざまな原因による死を勘案してこのモデルを一般化した結果である．Gompertz–Makeham分布はいわゆるGompertz–Makehamの寿命の法則の基礎となったものである．この法則は，人間の死亡率は年齢に依存するものと年齢には依存しないものの2成分からなるとする．この法則は，コンピュータサイエンス，保険数理，老年学，人口統計，生物学，信頼性理論を含むさまざまな分野で使用されている．
  • RandomVariateを使って，Gompertz–Makeham分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,GompertzMakehamDistribution[λ,ξ,θ,α]]（より簡略すると xGompertzMakehamDistribution[λ,ξ,θ,α]）を使って，確率変数 x が，Gompertz–Makeham分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[GompertzMakehamDistribution[λ,ξ,θ,α],x]およびCDF[GompertzMakehamDistribution[λ,ξ,θ,α],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がGompertz–Makeham分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックGompertz–Makeham分布を推定することが，FindDistributionParametersを使ってデータをGompertz–Makeham分布にフィットすることができる．ProbabilityPlotを使って記号Gompertz–Makeham分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号Gompertz–Makeham分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたGompertz–Makeham分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってGompertz–Makeham分布を含む高次元分布を構築することが，ProductDistributionを使ってGompertz–Makeham分布を含む独立成分分布の結合分布を計算することができる．
  • Gompertz–Makeham分布は，他のいくつかの分布と関連がある．例えば，GompertzMakehamDistributionは，GompertzMakehamDistribution[λ,θ/λ]のハザード関数（HazardFunctionを参照のこと）は，λ がゼロに近付くに従ってExponentialDistribution[θ]に近付くという意味で，ExponentialDistributionと関連がある．これに加え，GompertzMakehamDistributionは切断GumbelDistributionである（つまり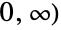，[に限定されたGumbelDistribution[a,b]はGompertzMakehamDistribution[1/b,Exp[-a/b]]と同じである）．この分布は切断WeibullDistributionと関係があり，したがって，FrechetDistribution，ExtremeValueDistributionを含む他の「極値分布」とも関係がある．GompertzMakehamDistributionは，GammaDistribution，ExpGammaDistribution，RayleighDistribution，StudentTDistributionとも関係がある．

例題

すべて開くすべて閉じる

例  (6)

Gompertz分布の確率密度関数：

Gompertz分布の累積分布関数：

Gompertz–Makeham分布の確率密度関数：

Gompertz–Makeham分布の累積分布関数：

Gompertz分布の平均と分散：

Gompertz分布の中央値：

スコープ  (10)

Gompertz分布にから擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

Gompertz分布の歪度：

Gompertz分布の尖度：

母数の関数としての閉形式のGompertz分布の種々のモーメント：

Moment：

CentralMoment：

FactorialMoment：

Cumulant：

Gompertz分布のハザード関数：

Gompertz–Makeham分布のハザード関数：

Gompertz分布の分位関数：

Gompertz–Makeham分布の分位関数：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

平均サービス時間を求める：

アプリケーション  (4)

寿命がGompertz分布に従うデバイスがある．このデバイスの信頼性を求める：

ハザード関数は時間とともに増大する：

直列のこのようなデバイス2つの信頼性を求める：

並列のこのようなデバイス2つの信頼性を求める：

と の2つの系の信頼性を比較する：

腐食作用に晒されていて n 個の微細な穴のいずれかが表面に達すると役に立たなくなる，厚みが θ のスチールパイプがある．各穴が表面に達するまでの時間は因数 k で残りの厚みに比例すると仮定する．それぞれの穴の深さが最初はランダムであり，時間の深さが母数 λ の右切断指数分布に従うなら，パイプが使えなくなるまでの時間はGompertz分布に従う．このパイプの信頼性を求める：

パイプが使えなくなるまでの平均時間を求める：

保険計理士協会によると1900年の女性の死亡率は次の表で与えられる：

最大尤度推定を使うためにサンプル母集団を作る：

Gompertz–Makeham分布をデータにフィットする：

確率密度関数をプロットする：

死亡率データを推定分布の生存関数と比較する：

1900年における女性の平均寿命を求める：

データと推定分布の平均残留寿命を比較する：

Gompertz分布を使って指数ベキ分布を定義する：

ハザード関数：

生存関数：

確率密度関数：

WeibullDistributionは極限のケースである：

特性と関係  (9)

GompertzMakehamDistributionは正の因子によるスケーリングの下では閉じている：

Gompertz分布族は最小値の下で閉じている：

さまざまな脆弱性の母数について：

Gompertz–Makeham分布族は最小値の下で閉じている：

さまざまな脆弱性の母数について：

他の分布との関係：

Gompertz分布は指数分布に関連している：

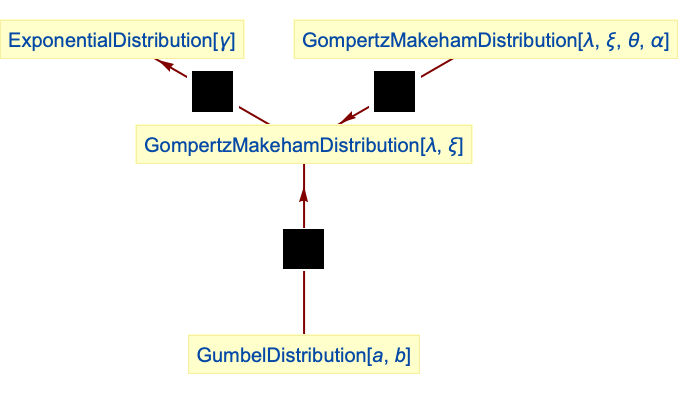
Gompertz–Makeham分布を θ=0と α=0について簡約するとGompertz分布になる：

Gompertz分布は切断GumbelDistributionである：

Gompertz分布は切断WeibullDistribution分布に関連している：

WeibullDistributionはGompertz分布に関連している：

おもしろい例題  (1)

累積分布関数の等高線を持つ λ のさまざまな値についての確率密度関数：

Wolfram Research (2010), GompertzMakehamDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/GompertzMakehamDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), GompertzMakehamDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/GompertzMakehamDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "GompertzMakehamDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GompertzMakehamDistribution.html.

APA

Wolfram Language. (2010). GompertzMakehamDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GompertzMakehamDistribution.html

BibTeX

@misc{reference.wolfram_2024_gompertzmakehamdistribution, author="Wolfram Research", title="{GompertzMakehamDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GompertzMakehamDistribution.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gompertzmakehamdistribution, organization={Wolfram Research}, title={GompertzMakehamDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/GompertzMakehamDistribution.html}, note=[Accessed: 18-November-2024 ]}