GumbelDistribution

GumbelDistribution[α,β]

位置母数 α，尺度母数 β のガンベル(Gumbel)分布を表す．

GumbelDistribution[]

位置母数0，尺度母数1のガンベル分布を表す．

詳細

  • ガンベル分布は正規分布等の分布から取ったサンプルの最小値の漸近分布を与える．
  • 時にガンベル分布とも呼ばれる最大値の漸近分布が，ExtremeValueDistributionとしてWolfram言語に実装されている． »
  • ガンベル分布における値 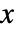の確率密度は 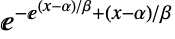に比例する． »
  • GumbelDistributionでは，α は任意の実数，β は任意の正の実数でよい．
  • GumbelDistributionでは，α と β は単位次元が等しい任意の数量でよい． »
  • GumbelDistributionは，Mean，CDF，RandomVariate等の関数で使うことができる． »

予備知識

  • GumbelDistribution[α,β]は，実数上で定義され，実数 α （「位置母数」）および正の実数 β （尺度母数）でパラメータ化された連続統計分布を表す．ガンベル分布の確率密度関数(PDF)は単峰性で，母数 α がPDFの水平位置を，母数 β がPDFの全体的な高さと傾きを決定する．PDFの裾部は，PDFが 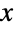の大きい値について指数的に減少するという意味で「薄い」（この動作は，分布のSurvivalFunctionを分析することで数量的に正確にできる）．ガンベル分布は，タイプ1の極値分布（Wolfram言語にExtremeValueDistributionとして実装されている極値分布と混同してはならない），二重指数分布（二重指数分布と呼ばれることがあるLaplaceDistributionと混同してはならない），対数ワイブル分布（WeibullDistributionを参照のこと）と呼ばれることがある．
  • GumbelDistributionは，「極値分布」としてまとめられる4つの分布の1つである（他の3つはFrechetDistribution，ExtremeValueDistribution，WeibullDistribution）．これらはすべて，「極端」あるいは「稀」な事象（例えば，中央値から甚だしく逸脱した偏差を含む変量からなるデータ集合を持つ「非常に可能性が低い」事象）の数量化に使われる．ガンベル分布はドイツ人の数学者であるEmil Julius Gumbelにちなんで命名された．Gumbelは，1930年代の終りに，この分布を，最小順序統計量のための極限分布（つまり，他の隠れた分布に従うサンプルの最小値についての潜在的な漸近分布）として研究した．ガンベル分布は，その始まりから，人間の寿命，放射線の放出，進化的な遺伝子変異，洪水と地震の分析，旱魃，破滅的な保険の損失等，現実世界の数多くの現象のモデル化に使われた．ガンベル分布は，整数論の整数分割（IntegerPartitionsを参照のこと）における項数や記録的な素数間隔の大きさの近似等にも使われてきた．
  • RandomVariateを使って，ガンベル分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,GumbelDistribution[α,β]]（より簡略すると xGumbelDistribution[α,β]）を使って，確率変数 x が，ガンベル分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[GumbelDistribution[α,β],x]およびCDF[GumbelDistribution[α,β],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がガンベル分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックガンベル分布を推定することが，FindDistributionParametersを使ってデータをガンベル分布にフィットすることができる．ProbabilityPlotを使って記号ガンベル分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号ガンベル分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたガンベル分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってガンベル分布を含む高次元分布を構築することが，ProductDistributionを使ってガンベル分布を含む独立成分分布の結合分布を計算することができる．
  • ガンベル分布は他のいくつかの分布と関係している．先述したように，GumbelDistributionはExtremeValueDistribution，FrechetDistribution，WeibullDistributionと定性的関係を共有している．これらの関係は，GumbelDistribution[α,β]のPDFがTransformedDistribution[-u,u ExtremeValueDistribution[-α,β]]およびTransformedDistribution[β α Log[u/β]+α,u WeibullDistribution[α,β]]のPDFと厳密に等しく，FrechetDistributionがWeibullDistributionの変換である点に注目することで，数量化することができる． GumbelDistributionは，GumbelDistribution[α,β]，MinStableDistribution[α,β,0]，TransformedDistribution[-u,u MaxStableDistribution[-α,β,0]]のPDFがすべて等しいという意味で，MinStableDistributionおよびMaxStableDistributionに関係している．GumbelDistributionはLogisticDistribution，ExpGammaDistribution，GompertzMakehamDistribution，ExponentialDistributionとも関係がある．

例題

すべて開くすべて閉じる

例  (4)

確率密度関数：

累積分布関数：

平均と分散：

中央値：

スコープ  (7)

ガンベル分布からの擬似乱数のサンプルを生成する：

そのヒストグラムと確率密度関数を比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度と尖度は一定である：

母数の関数としての閉形式の種々のモーメント：

Moment：

CentralMoment：

FactorialMoment：

Cumulant：

記号次数の閉形式：

ハザード関数：

分位関数：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

価格の平均と標準偏差を計算する：

アプリケーション  (2)

寿命がガンベル分布に従うデバイスがある．このデバイスの信頼性を求める：

ハザード関数は時間とともに指数関数的に増大する：

直列のこのようなデバイス2つの信頼性を求める：

並列のこのようなデバイス2つの信頼性を求める：

と について2つの系の信頼性を比較する：

1年のうちで最大の地震のマグニチュードはGumbelDistributionでモデル化することができる．合衆国の過去200年間の地震について考察する：

年間最大のものを求める：

欠測データを除いてサンプルを作成する：

ガンベル分布をデータにフィットする：

サンプルのヒストグラムを推定分布の確率密度関数と比較する：

マグニチュードが最低6の年間最大地震の確率を求める：

年間最大地震の平均マグニチュードを求める：

年間の最大地震のマグニチュードのシミュレーションを30年間分行う：

特性と関係  (15)

ガンベル分布は平行移動と正の因子によるスケーリングの下では閉じている：

歪度はExtremeValueDistributionの歪度に負号を付けたものである：

ExtremeValueDistributionは右に歪んでいるのに対しGumbelDistributionは左に歪んでいる：

尖度はExtremeValueDistributionのものに等しい：

GumbelDistribution族は最小値の下で閉じている：

GumbelDistributionの累積分布関数は最小の安定性の仮定の方程式を解く：

と を求める：

他の分布との関係：

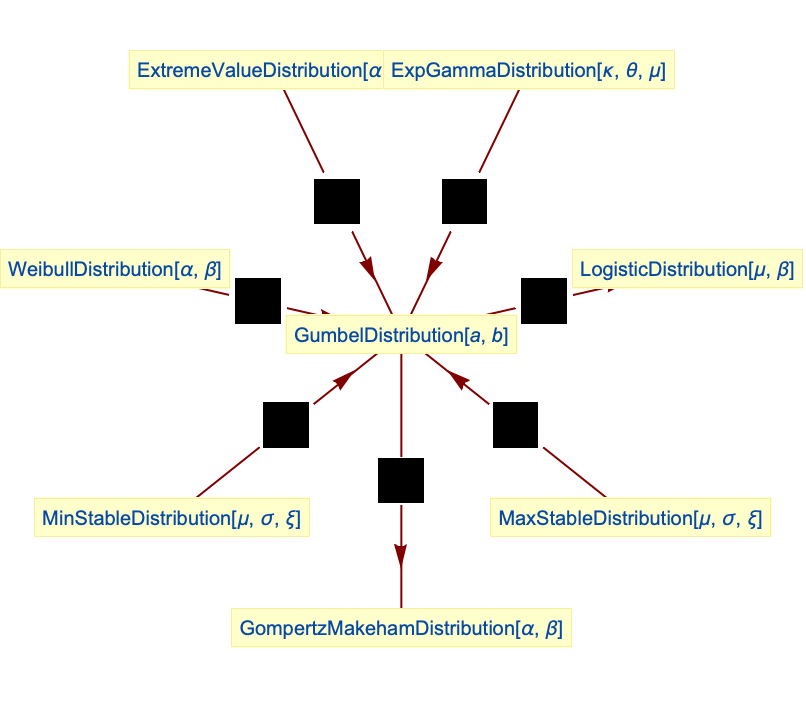
GumbelDistributionはExtremeValueDistributionの否定である：

GumbelDistributionはWeibullDistributionを変換したものである：

切断ガンベル分布はGompertzMakehamDistributionである：

GumbelDistributionはMinStableDistributionの特殊ケースである：

GumbelDistributionはMaxStableDistributionを変換したものである：

GumbelDistributionに従う2変量の差はExtremeValueDistributionに従う2変量の差が従う分布，すなわちLogisticDistributionに従う：

ガンベル分布とExtremeValueDistributionの和はLogisticDistributionに従う：

GumbelDistributionはExpGammaDistributionの特殊ケースである：

ガンブル分布を含むExtremeValueDistributionのParameterMixtureDistributionは，LogisticDistributionに従う：

考えられる問題  (3)

最小値の分布はGumbelDistributionで与えられる：

最大値の分布はExtremeValueDistributionで与えられる：

GumbelDistributionは，α が実数ではないときは定義されない：

GumbelDistributionは，β が正の実数ではないときは定義されない：

記号出力に無効な母数を代入すると意味のない結果が返される：

おもしろい例題  (1)

累積分布関数の等高線を持つ α のさまざまな値についての確率密度関数：

Wolfram Research (2007), GumbelDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/GumbelDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2007), GumbelDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/GumbelDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2007. "GumbelDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/GumbelDistribution.html.

APA

Wolfram Language. (2007). GumbelDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GumbelDistribution.html

BibTeX

@misc{reference.wolfram_2024_gumbeldistribution, author="Wolfram Research", title="{GumbelDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/GumbelDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gumbeldistribution, organization={Wolfram Research}, title={GumbelDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/GumbelDistribution.html}, note=[Accessed: 22-November-2024 ]}