HypergeometricDistribution
HypergeometricDistribution[n,nsucc,ntot]
表示超几何分布.
更多信息
- 超几何分布给出从总数目为 ntot、其中成功数为 nsucc 的总体中抽取 n 次所得到的成功次数的分布.
- HypergeometricDistribution 允许 n、nsucc 和 ntot 为任意整数,且满足 0<n≤ntot 和 0≤nsucc≤ntot.
- HypergeometricDistribution 可以和 Mean、CDF 和 RandomVariate 这样的函数一起使用.. »
背景
- HypergeometricDistribution[n,nsucc,ntot] 表示整数值
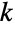 的离散统计分布,也称超几何分布,其中
的离散统计分布,也称超几何分布,其中 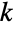 满足
满足 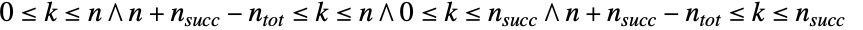 . 分布由满足条件 0<n≤ntot 和 0≤nsucc≤ntot 的整数参数 n、nsucc 和 ntot 决定,它们分别表示实验从样本中抽取的次数,整体样本中成功的数量和样本大小. 超几何分布的概率密度函数(PDF)是离散和单峰的. 此分布有时也被称为中心或典型超几何分布,以便和相关及质量相似的 Wallenius 分布(WalleniusHypergeometricDistribution)、Fisher 分布(FisherHypergeometricDistribution)区分.
. 分布由满足条件 0<n≤ntot 和 0≤nsucc≤ntot 的整数参数 n、nsucc 和 ntot 决定,它们分别表示实验从样本中抽取的次数,整体样本中成功的数量和样本大小. 超几何分布的概率密度函数(PDF)是离散和单峰的. 此分布有时也被称为中心或典型超几何分布,以便和相关及质量相似的 Wallenius 分布(WalleniusHypergeometricDistribution)、Fisher 分布(FisherHypergeometricDistribution)区分. - 超几何分布给出了在含有 nsucc 个成功物件的,总数为 ntot 个物件的样本中(无放回)抽取 n 次抽到成功物件数量的分布. 它可以用瓮模型可视化,即从一个有 nsucc 个蓝球 ntot-nsucc 个绿球的的瓮中无放回的摸取 n 个球. 超几何分布可以追溯到棣莫弗(de Moivre)在1710年代的工作,该分布是他从更早的惠更斯(Huygens)提出的、和上述瓮问题相关的瓮问题中求得的解. 超几何分布的名字来自于这样一个事实:它的 PDF 可以用广义超几何函数(Hypergeometric2F1)表示,而分布本身则被用于对各种领域的若干数量建模. 特别的,超几何分布已被用作排队模型,制造系统,人口动态,列联表分析和量子密码等的研究工具.
- RandomVariate 可被用于给出超指数分布的一个或多个机器精度或任意精度(后者可用 WorkingPrecision 选项指定)的伪随机变量. Distributed[x,HypergeometricDistribution[n,nsucc,ntot]],更简洁的写法是 xHypergeometricDistribution[n,nsucc,ntot],可被用于声明随机变量 x 是超指数分布的. 这样一个声明之后可用在如 Probability、NProbability、Expectation 以及 NExpectation 这样的函数中.
- 概率密度函数和累积分布函数可用 PDF[HypergeometricDistribution[n,nsucc,ntot],x] 和 CDF[HypergeometricDistribution[n,nsucc,ntot],x] 求得,虽然可以注意到它的 PDF 没有解析表达式. 平均数、中位数、方差、原点矩及中心矩可分别用 Mean、Median、Variance、Moment 和 CentralMoment 计算. 这些量可以用 DiscretePlot 可视化.
- DistributionFitTest 可被用于测试给定的数据集是否与超指数分布一致,EstimatedDistribution 可被用于根据给定数据估算超指数参数化分布,而 FindDistributionParameters 可拟合数据和超指数分布. ProbabilityPlot 可被用于生成给定数据的 CDF 相对于符号超指数分布的 CDF 的图线,而 QuantilePlot 可被用于生成给定数据的分位数相对于符号超指数分布的分位数的图线.
- TransformedDistribution 可被用于表示转换的超指数分布,CensoredDistribution 可被用于表示删截后位于上限值和下限值之间的值分布,而 TruncatedDistribution 可被用于表示截断后位于上限值和下限值之间的值分布. CopulaDistribution 可被用于建立包含了超指数分布的高维分布,而 ProductDistribution 可被用于计算包括超指数分布在内的,若干个独立分量的联合概率分布.
- HypergeometricDistribution 和许多其它统计分布有关. 例如, HypergeometricDistribution 同时被 FisherHypergeometricDistribution 和 WalleniusHypergeometricDistribution 推广,意思是 HypergeometricDistribution[n,nsucc,ntot] 和 FisherHypergeometricDistribution[n,nsucc,ntot,1] 及 WalleniusHypergeometricDistribution[n,nsucc,ntot,1] 有相同的 PDF. 当
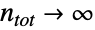 时,HypergeometricDistribution 的极限分布是 BinomialDistribution,而 MultivariateHypergeometricDistribution 显然是 HypergeometricDistribution 的高维推广. HypergeometricDistribution 还和 GeometricDistribution、NormalDistribution、PoissonDistribution、PearsonDistribution 及 BetaBinomialDistribution 有关.
时,HypergeometricDistribution 的极限分布是 BinomialDistribution,而 MultivariateHypergeometricDistribution 显然是 HypergeometricDistribution 的高维推广. HypergeometricDistribution 还和 GeometricDistribution、NormalDistribution、PoissonDistribution、PearsonDistribution 及 BetaBinomialDistribution 有关.
范例
打开所有单元关闭所有单元范围 (7)
应用 (6)
HypergeometricDistribution 的 CDF 是右连续函数的一个例子:
一次抽取 50 个元素,计算其中有超过 25 个特殊元素的概率:
假设在 10 个物品中,有 5 个有缺陷,取 6 个物品作检测. 对所发现有缺陷的物品数进行计数,对该测试过程进行模拟:
一次抽奖卖 10 张彩票,每张售价 1 美元. 每次抽奖只有一张彩票中奖. 一个赌徒只有 5 美元用来消费. 如果他所购买的 5 张票分别属于 5 次不同的抽奖,求他的中奖概率:
一个容器包含 ![]() 个白球和 1 个蓝球. 两个选手从容器中不放回式的抽球,直到抽到蓝球. 抽取蓝球的选手获胜. 求抽取第一个球的选手获胜的几率. 假设第一个选手在第
个白球和 1 个蓝球. 两个选手从容器中不放回式的抽球,直到抽到蓝球. 抽取蓝球的选手获胜. 求抽取第一个球的选手获胜的几率. 假设第一个选手在第 ![]() 次抽取时获胜,前
次抽取时获胜,前 ![]() 次抽取是白球的概率服从 HypergeometricDistribution:
次抽取是白球的概率服从 HypergeometricDistribution:
属性和关系 (8)
超几何分布的特征函数是根据 Hypergeometric2F1 来定义的:
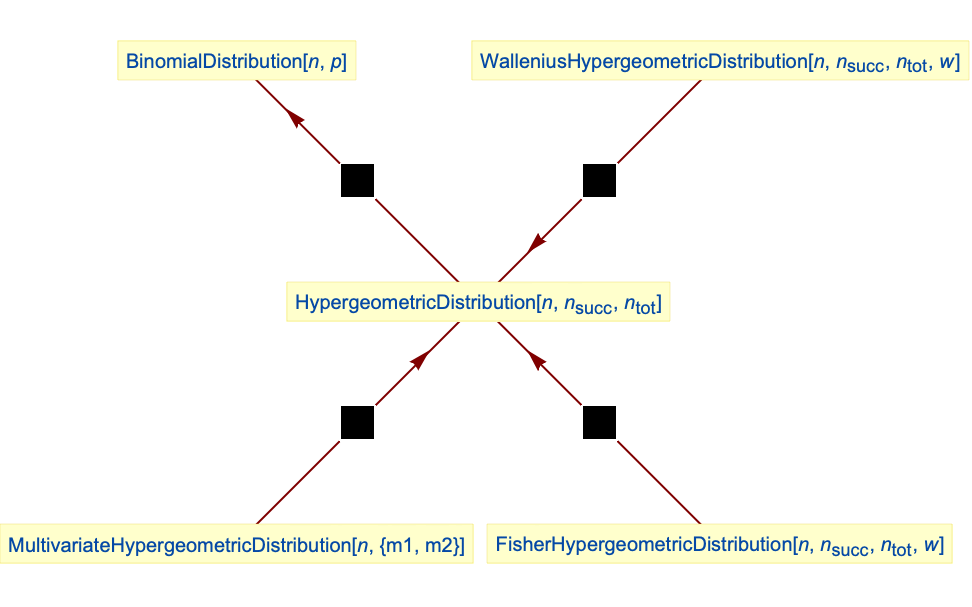
HypergeometricDistribution 无限大样本量下的极限是 BinomialDistribution:
超几何分布是 FisherHypergeometricDistribution 的一个特例:
超几何分布是 WalleniusHypergeometricDistribution 的一个特例:
超几何分布等价于二元 MultivariateHypergeometricDistribution:
HypergeometricDistribution 可以从两个独立二项分布的变量在已知它们的和的条件下求得:
可能存在的问题 (4)
当 ntot、nsucc 或者 n 非正时,HypergeometricDistribution 没有定义:
当 n>ntot 时,HypergeometricDistribution 没有定义:
当 nsucc>ntot 时,HypergeometricDistribution 没有定义:
文本
Wolfram Research (2007),HypergeometricDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/HypergeometricDistribution.html.
CMS
Wolfram 语言. 2007. "HypergeometricDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/HypergeometricDistribution.html.
APA
Wolfram 语言. (2007). HypergeometricDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/HypergeometricDistribution.html 年