InfinitePlane

InfinitePlane[{p1,p2,p3}]

点 p1，p2，p3を通る平面を表す．

InfinitePlane[p,{v1,v2}]

点 p を通り v1および v2の方向へ向かう平面を表す．

詳細

  • InfinitePlaneは平面あるいは超平面としても知られている．
  • InfinitePlaneは，幾何学領域として，あるいはグラフィックスプリミティブとして使うことができる．
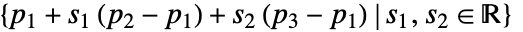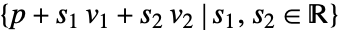  • InfinitePlaneは，平面あるいはを表す．
  • Hyperplane[n,p]は3Dで法線 n を使った別の表現である．
  • InfinitePlaneは，GraphicsおよびGraphics3Dで使うことができる．
  • InfinitePlaneは，描画の際はPlotRangeで切り取られる．
  • グラフィックスでは，点 p，piおよびベクトル v はDynamic式でよい．
  • グラフィックスの描画は，FaceForm，Opacity，色等の指示子の影響を受ける．
  • FaceForm[front,back]を使って3Dの前景と背景に異なるスタイルを指定することができる．前景は規則の右辺と点 piあるいはベクトル viからの方向で定義される．
  • InfinitePlaneは，RegionMeasure，RegionCentroid等の関数で使うことができる．

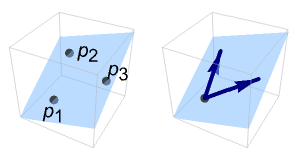
例題

すべて開くすべて閉じる

例  (3)

3DのInfinitePlane：

異なるスタイルを適用された無限平面：

点が指定された無限平面に属するかどうかを判断する：

スコープ  (17)

グラフィックス  (7)

指定  (2)

3つの点を使って3Dの無限平面を定義する：

1つの点と2つの接線ベクトルを使って同じ平面を定義する：

方向が異なる無限平面：

スタイリング  (2)

色指示子で無限平面の色を指定する：

FaceFormおよびEdgeFormを使って面と辺のスタイルを指定することができる：

座標  (3)

プロット範囲との割合で座標を指定する：

通常の座標からスケールされたオフセットを指定する：

点とベクトルはDynamicでよい：

領域  (10)

埋込み次元は座標の次元である：

幾何次元は領域自体の次元である：

点の帰属判定：

帰属条件を得る：

無限平面の測度は無限で重心は定義されない：

点からの距離：

点からの符号付き距離：

領域内の最近点：

最近点：

無限平面は有界ではない：

領域範囲を求める：

無限平面上で積分する：

無限平面上で最適化する：

無限平面上で方程式を解く：

アプリケーション  (7)

三角形が埋め込まれている平面を求める：

InfinitePlaneはTriangleと同じパラメータ化を使うことができる：

多角形が埋め込まれている平面を求める：

平面を求めるためには，最初の3点（あるいは同じ直線上にはない任意の3点）を取る：

パラメトリック曲面 f[u,v]の接平面はInfinitePlane[f[u,v],{∂uf[u,v],∂vf[u,v]}]で与えられる．パラメトリック曲面の接平面を求める：

曲面の接平面を求める：

で定義される，球，平面，曲面の交点を求める：

交点を可視化する：

BubbleChartの空間を分割する：

グラフィックスを組み合せる：

反射面を可視化する：

反射面を定義する：

平面上の点とその法線ベクトルを使ってReflectionTransformを定義する：

平面についての単位立方体の反射を可視化する：

特性と関係  (6)

InfinitePlane[{p1,p2,p3}]はInfinitePlane[p1,{p2-p1,p3-p1}]に等しい：

InfinitePlane[p,{v1,v2}]は3DのHyperplane[Cross[v1,v2],p]に等しい：

ParametricRegionは，任意のInfinitePlaneを表すことができる：

ImplicitRegionは任意のInfinitePlaneを表すことができる：

InfinitePlaneはConicHullRegionの特殊ケースである：

任意のInfinitePlaneを2つのHalfPlane領域の和集合で表すことができる：

おもしろい例題  (2)

平面のランダムな集合：

無限平面を軸の周りで急速に動かす：

Wolfram Research (2014), InfinitePlane, Wolfram言語関数， https://reference.wolfram.com/language/ref/InfinitePlane.html （2016年に更新）.

テキスト

Wolfram Research (2014), InfinitePlane, Wolfram言語関数， https://reference.wolfram.com/language/ref/InfinitePlane.html （2016年に更新）.

CMS

Wolfram Language. 2014. "InfinitePlane." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/InfinitePlane.html.

APA

Wolfram Language. (2014). InfinitePlane. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InfinitePlane.html

BibTeX

@misc{reference.wolfram_2024_infiniteplane, author="Wolfram Research", title="{InfinitePlane}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/InfinitePlane.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_infiniteplane, organization={Wolfram Research}, title={InfinitePlane}, year={2016}, url={https://reference.wolfram.com/language/ref/InfinitePlane.html}, note=[Accessed: 22-November-2024 ]}