InhomogeneousPoissonPointProcess

InhomogeneousPoissonPointProcess[μ,d]

における密度関数が の非同次ポアソン(Poisson)点過程を表す．

詳細

  • InhomogeneousPoissonPointProcessは，非定常ポアソン点過程あるいは独立散乱点過程としても知られている．
  • 一般的な用途には，さまざまな成長条件等，場所 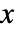のみに依存するさまざまな密度のモデリングが含まれる．
  • InhomogeneousPoissonPointProcessは，指定された密度関数 μ に従って，点の相互作用なしで領域内に点を生成する．
  • 密度関数 μ を使うと，観測領域 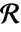における点の数は平均 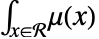でPoissonDistributionに従って分布する．
  • 密度関数 μ は以下として与えることができる．
  • funcベクトルの関数
    geofunc地理的場所の関数
    PointDensityFunction点集合からの密度関数
  • 互いに素な領域 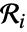におけるポアソン点過程の点の数 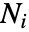は，独立した 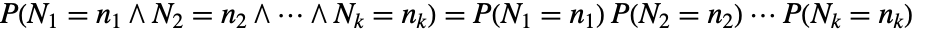である．ただし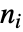，は非負の整数である．
  • 密度関数 μ での体積 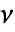の観測領域 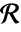における点配置の密度関数はPoissonPointProcess[1,d]について 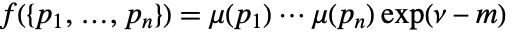である．
  • 点 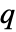を点集合に加える際のPapangelou条件密度 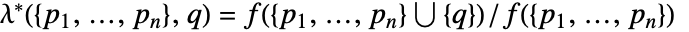は，密度関数が μ の非同次ポアソン点過程については 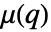である．
  • 密度関数 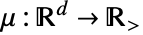は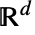，内の任意の正の整数関数でよく，d は任意の正の整数でよい．
  • InhomogeneousPoissonPointProcessは，RipleyKやRandomPointConfiguration等の関数と一緒に使うことができる．

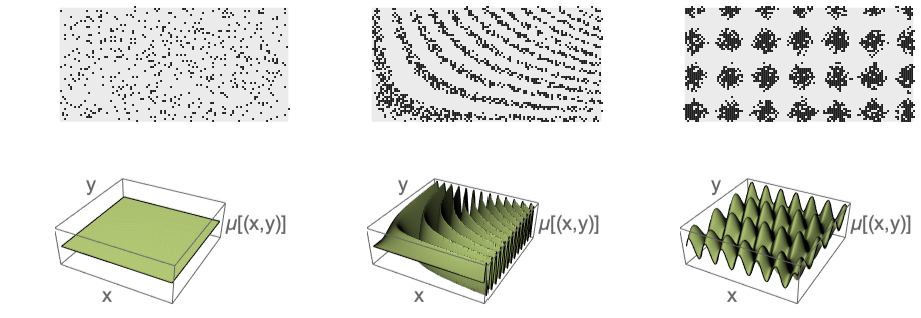
例題

すべて開くすべて閉じる

例  (4)

InhomogeneousPoissonPointProcessからサンプルを取る：

地球表面上で定義されたInhomogeneousPoissonPointProcessからサンプルを取る：

点を可視化する：

ノンパラメトリック点密度からサンプルを取る：

ビン分割された密度からサンプルを取る：

計算された点密度関数で点過程を定義し，有効かどうかをチェックする：

複数の点配置のシミュレーションを行う：

スコープ  (4)

いくつかの実現のシミュレーションを行う：

RegionEmbeddingDimensionがそのRegionDimensionと等しい任意の有効なRegionQからサンプルを取る：

領域条件をチェックする：

点のサンプル：

ガウス散乱は等方性非同次ポアソン点過程の例である：

長方形上でこの過程のシミュレーションを行う：

PointCountDistributionは原点の周りの回転について不変である：

回転された領域における点の数の分布：

この分布は同じ方法で識別されたものと同じである：

区分密度を定義する：

過程を定義する：

この過程からサンプルを取る：

オプション  (1)

Method  (1)

異なるメソッドを使ってInhomogeneousPoissonPointProcessからサンプルを取る：

細線化法を使う：

マルコフ(Markov)鎖モンテカルロ法を使う：

領域上でサンプルをプロットする：

アプリケーション  (2)

断層線のような線までの距離に依存する密度を持つ点過程：

点過程を定義する：

過程のシミュレーションを行う：

木の周りに落ちたタネの可能な点パターンのシミュレーションを行う：

点過程を定義する：

過程のシミュレーションを行う：

タネのパターンのシミュレーションを行う：

特性と関係  (5)

密度が一定の非同次ポアソン点過程を評価すると自動的にPoissonPointProcessになる：

InhomogeneousPoissonPointProcessについての領域の中の点の期待数はPoissonDistributionに従う：

領域上の点の数の分布を計算する：

円板上：

陰的領域上：

非同次ポアソン点過程についてのボイド確率を計算する：

長方形について：

平行移動された長方形について：

非同次ポアソン点過程は定常ではなく，密度は位置に依存する：

部分領域における点の数の分布：

平行移動された部分領域における点の数の分布：

領域の測度は同じである：

PointCountDistributionで表される密度は異なる：

一定密度関数のInhomogeneousPoissonPointProcessはPoissonPointProcessである：

円板上の点の数の分布：

同じ領域における対応するポアソン点過程についての点の数の分布：

より高次元で：

球体内の点の数の分布：

同じ領域における対応するポアソン点過程についての点の数の分布：

おもしろい例題  (1)

領域に依存する密度を使う：

Wolfram Research (2020), InhomogeneousPoissonPointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html.

テキスト

Wolfram Research (2020), InhomogeneousPoissonPointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html.

CMS

Wolfram Language. 2020. "InhomogeneousPoissonPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html.

APA

Wolfram Language. (2020). InhomogeneousPoissonPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html

BibTeX

@misc{reference.wolfram_2024_inhomogeneouspoissonpointprocess, author="Wolfram Research", title="{InhomogeneousPoissonPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inhomogeneouspoissonpointprocess, organization={Wolfram Research}, title={InhomogeneousPoissonPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/InhomogeneousPoissonPointProcess.html}, note=[Accessed: 18-November-2024 ]}