InverseChiSquareDistribution
InverseChiSquareDistribution[ν]
自由度 ν の逆カイ二乗(![]() )分布を表す.
)分布を表す.
InverseChiSquareDistribution[ν,ξ]
スケールされた逆カイ二乗(![]() )分布(自由度 ν,スケール ξ)を表す.
)分布(自由度 ν,スケール ξ)を表す.
詳細

- 逆カイ二乗(
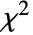 )分布InverseChiSquareDistribution[ν]はカイ二乗(
)分布InverseChiSquareDistribution[ν]はカイ二乗(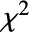 )分布に従う自由度 ν の確率変数の逆分布に従う分布である.
)分布に従う自由度 ν の確率変数の逆分布に従う分布である. - 数量
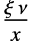 はスケールされた逆カイ二乗(
はスケールされた逆カイ二乗(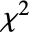 )分布InverseChiSquareDistribution[ν,ξ]に従う.ただし
)分布InverseChiSquareDistribution[ν,ξ]に従う.ただし 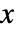 は自由度 ν のカイ二乗(
は自由度 ν のカイ二乗(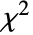 )分布に従う. »
)分布に従う. » - 逆カイ二乗(
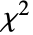 )分布は一般にベイズ(Bayes)データ解析の正規モデルに使われる.
)分布は一般にベイズ(Bayes)データ解析の正規モデルに使われる. - InverseChiSquareDistributionでは ν と ξ は任意の正の実数である.
- InverseChiSquareDistributionでは,ξ は任意の単位次元の数量でよく,ν は無次元量でよい. »
- InverseChiSquareDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- InverseChiSquareDistribution[ν,ξ]は,区間
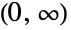 上で定義され,分布の自由度と尺度をそれぞれ表す正の値 ν と ξ でパラメータ化され,スケールされた逆カイ二乗(逆
上で定義され,分布の自由度と尺度をそれぞれ表す正の値 ν と ξ でパラメータ化され,スケールされた逆カイ二乗(逆 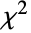 )分布として知られる連続統計分布を表す.スケールされた逆カイ二乗分布の確率密度関数(PDF)は,大体において単一の「峰」(最大値)を持つ単峰性である.その全体的な形(高さ,広がり,
)分布として知られる連続統計分布を表す.スケールされた逆カイ二乗分布の確率密度関数(PDF)は,大体において単一の「峰」(最大値)を持つ単峰性である.その全体的な形(高さ,広がり,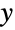 軸の周辺での集中度))は ν と ξ の値で決まる.加えて,スケールされた逆カイ二乗関数のPDFの裾部は,
PDFが
軸の周辺での集中度))は ν と ξ の値で決まる.加えて,スケールされた逆カイ二乗関数のPDFの裾部は,
PDFが 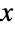 の大きい値について指数的というより代数的に減少するという意味で「太い」(この動作は分布のSurvivalFunctionを分析することで数量的に正確にすることができる).1母数が1つの形のInverseChiSquareDistribution[ν](これはInverseChiSquareDistribution[ν,1/ν]に等しい)は,スケールされていないスケールされていない逆カイ二乗分布と呼ばれることもあるが,最も一般的には「逆カイ二乗分布そのもの」と呼ばれる.
の大きい値について指数的というより代数的に減少するという意味で「太い」(この動作は分布のSurvivalFunctionを分析することで数量的に正確にすることができる).1母数が1つの形のInverseChiSquareDistribution[ν](これはInverseChiSquareDistribution[ν,1/ν]に等しい)は,スケールされていないスケールされていない逆カイ二乗分布と呼ばれることもあるが,最も一般的には「逆カイ二乗分布そのもの」と呼ばれる. - InverseChiSquareDistribution[ν]は,カイ二乗確率変数の逆数が従う分布である.これに対し,InverseChiSquareDistribution[ν,ξ]は,
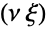 でスケールされたそのような確率変数の逆数が従う分布である.表現を変えるなら,
でスケールされたそのような確率変数の逆数が従う分布である.表現を変えるなら,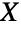 が確率変数で
が確率変数で 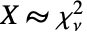 (
(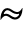 は「に従って分布する」を表す)なら,
は「に従って分布する」を表す)なら,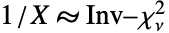 かつ
かつ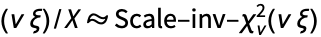 である.ベイズ確率では,逆カイ二乗分布は,分散が未知である正規分布に従うデータの推論のために,事前分布としても事後分布としても使用される.この分布は分類理論におけるフィッシャー法の統計的基礎としても持ちられる.InverseChiSquareDistributionは,モンテカルロ法,金融数学,計量心理学,電気工学を含む多くの分野でツールとしても使われている.
である.ベイズ確率では,逆カイ二乗分布は,分散が未知である正規分布に従うデータの推論のために,事前分布としても事後分布としても使用される.この分布は分類理論におけるフィッシャー法の統計的基礎としても持ちられる.InverseChiSquareDistributionは,モンテカルロ法,金融数学,計量心理学,電気工学を含む多くの分野でツールとしても使われている. - RandomVariateを使って,逆カイ二乗分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,InverseChiSquareDistribution[ν,ξ]](より簡略な表記では xInverseChiSquareDistribution[ν,ξ])を使って,確率変数 x が逆カイ二乗分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 逆カイ二乗分布の確率密度関数および累積分布関数は,PDF[InverseChiSquareDistribution[ν,ξ],x]およびCDF[InverseChiSquareDistribution[ν,ξ],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合が逆カイ二乗分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリック逆カイ二乗分布を推定することが,FindDistributionParametersを使ってデータを逆カイ二乗分布にフィットすることができる.ProbabilityPlotを使って記号逆カイ二乗分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号逆カイ二乗分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換された逆カイ二乗分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使って逆カイ二乗分布を含む高次元分布を構築することが,ProductDistributionを使って逆カイ二乗分布を含む独立成分分布の結合分布を計算することができる.
- InverseChiSquareDistributionは他の数多くの分布と密接に関係している.例えば,GammaDistribution,ExponentialDistribution,ChiSquareDistribution,UniformDistribution,LaplaceDistributionを含むいくつかの分布は,InverseChiSquareDistributionの変換で得ることができる.また,NormalDistributionとFRatioDistributionはInverseChiSquareDistributionの変換バージョンの極限値である.さらに,InverseChiSquareDistributionはPearsonDistributionおよびInverseGammaDistributionの特殊バージョンとして,また,RayleighDistribution,MaxwellDistribution,ParetoDistributionを含む分布の変換された特殊ケースとして見ることができる.InverseChiSquareDistributionは,BetaDistribution,StudentTDistribution,UniformDistribution,NoncentralChiSquareDistributionとも密接に関係している.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
極限では,尖度はNormalDistributionの尖度に等しい:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (2)
平均0の正規分布の分散の事後分布は母数 ![]() ,尺度母数
,尺度母数 ![]() のInverseChiSquareDistributionであることが分かった.分散の最尤値を求める:
のInverseChiSquareDistributionであることが分かった.分散の最尤値を求める:
InverseChiSquareDistributionは平均が既知で分散が未知である正規分布の尤度の共役事前分布である:
事後分布は再び新たな母数 ![]() と
と ![]() を持つInverseChiSquareDistributionである:
を持つInverseChiSquareDistributionである:
特性と関係 (7)
InverseChiSquareDistributionは正の因子によるスケーリングの下では閉じている:
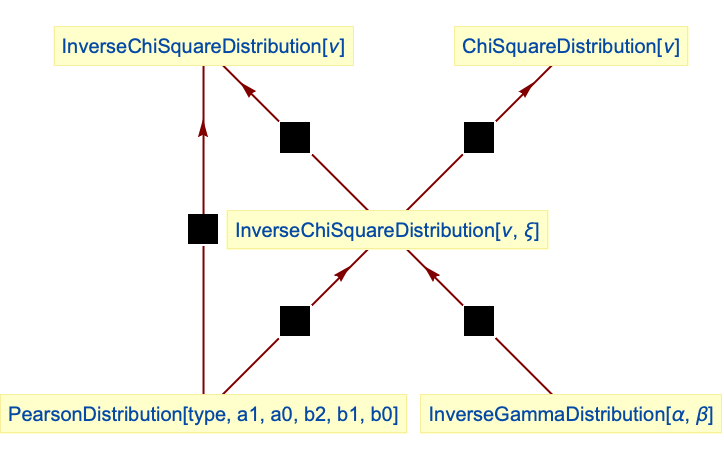
InverseChiSquareDistribution[ν]のスケールは ![]() である:
である:
InverseChiSquareDistributionはInverseGammaDistributionの特殊ケースである:
InverseChiSquareDistributionとChiSquareDistributionは互いに逆の関係にある:
InverseChiSquareDistributionはタイプ5のPearsonDistributionの特殊ケースである:
InverseChiSquareDistributionはタイプ5のPearsonDistributionの特殊ケースである:
考えられる問題 (2)
テキスト
Wolfram Research (2008), InverseChiSquareDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/InverseChiSquareDistribution.html (2016年に更新).
CMS
Wolfram Language. 2008. "InverseChiSquareDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/InverseChiSquareDistribution.html.
APA
Wolfram Language. (2008). InverseChiSquareDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InverseChiSquareDistribution.html