KumaraswamyDistribution
形状母数が α と β のKumaraswamy分布を表す.
詳細
- 値
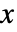 の確率密度は,
の確率密度は,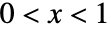 については
については 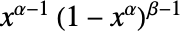 に比例し,その他ではゼロである.
に比例し,その他ではゼロである. - KumaraswamyDistributionでは,α と β は任意の正の実数でよい.
- KumaraswamyDistributionでは,α と β は無次元量でよい. »
- KumaraswamyDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- KumaraswamyDistribution[α,β]は,区間
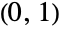 でサポートされ,確率密度関数(PDF)の全体的な動作を決定する「形状母数」として知られる正の実数 α および β によってパラメータ化された統計分布を表す.Kumaraswamy分布のPDFには,α および β の値によって,単一の「峰」(つまり,最大値)がある単峰性,単調増加,単調減少,(最小値を持ち全体的窪んでいる)潜在的な特異値が領域の境界に境界に近付く「浴槽型」がある.ベータ分布はKumaraswamyの二重境界分布と呼ばれることがあり,そのPDFがKumaraswamy分布のそれと数量的に似ているために,「ベータ分布(BetaDistribution)に似ている」とみなされることもある.
でサポートされ,確率密度関数(PDF)の全体的な動作を決定する「形状母数」として知られる正の実数 α および β によってパラメータ化された統計分布を表す.Kumaraswamy分布のPDFには,α および β の値によって,単一の「峰」(つまり,最大値)がある単峰性,単調増加,単調減少,(最小値を持ち全体的窪んでいる)潜在的な特異値が領域の境界に境界に近付く「浴槽型」がある.ベータ分布はKumaraswamyの二重境界分布と呼ばれることがあり,そのPDFがKumaraswamy分布のそれと数量的に似ているために,「ベータ分布(BetaDistribution)に似ている」とみなされることもある. - Kumaraswamy分布はインド人の水文学者であるPoondi Kumaraswamyによって開発され,1980年の論文で,それまで従来の分布あるいは経験分布によってうまく説明できなかった確率水文量の説明に適する一般化された分布として発表された.Kumaraswamy分布は,両側に境界を持ち,この2つの境界間に峰を持つことも持たないこともある確率変量をモデル化することができる.Kumaraswamy分布は,その理論的重要性に加え,水文学を含む幅広い地球科学に応用されており,電気工学,土木工学,機械工学,金融工学を含む工学のさまざまな分野における現象の説明に使われている.
- RandomVariateを使って,Kumaraswamy分布から,1つあるいは複数の機械精度あるいは(WorkingPrecisionオプションを介して)任意精度の擬似ランダム変量を与えることができる.Distributed[x,KumaraswamyDistribution[α,β]](より短縮した表記では xKumaraswamyDistribution[α,β])を使って,確率変数 x がKumaraswamy分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- Kumaraswamy分布についての確率密度関数および累積分布関数は,PDF[KumaraswamyDistribution[α,β],x]およびCDF[KumaraswamyDistribution[α,β],x]を使って与えることができる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って与えることができる.
- DistributionFitTestを使って,与えられたデータ集合がKumaraswamy分布と矛盾しないかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックKumaraswamy分布を推定することが,FindDistributionParametersを使ってデータをKumaraswamy分布にフィットすることができる.ProbabilityPlotを使って与えられたデータのCDFに対する記号Kumaraswamy分布のCDFのプロットを生成することが,QuantilePlotを使って与えられたデータの変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたベKumaraswamy分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってKumaraswamy分布を含む高次元分布を構築することが,ProductDistributionを使ってKumaraswamy分布を含む独立成分分布の結合分布を計算することができる.
- KumaraswamyDistributionは他の数多くの分布と密接な関係がある.BetaDistributionとの数量的な関係に加え,KumaraswamyDistributionはその母数のある種の値についてBetaDistributionに簡約することができる(例:PDF[KumaraswamyDistribution[1,β],x]はPDF[BetaDistribution[1,β],x]に等しく,PDF[KumaraswamyDistribution[α,1],x]はPDF[BetaDistribution[α,1],x]に等しい).同様に,KumaraswamyDistributionはある種のパラメータ化によってPowerDistributionに簡約することができ,これはBetaDistributionのTransformedDistributionを介した変換としても実現することができる.KumaraswamyDistribution[1,1]は厳密にUniformDistribution[{0,1}]であり,一般に,KumaraswamyDistributionは,ExponentialDistribution,PERTDistribution,PearsonDistribution,ChiSquareDistribution,GammaDistribution,FRatioDistribution,BetaPrimeDistributionに関連している.
例題
すべて開くすべて閉じるスコープ (8)
Kumaraswamy分布から擬似乱数のサンプルを生成する:
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
無次元Quantityを使ってKumaraswamyDistributionを定義する:
アプリケーション (1)
KumaraswamyDistributionは水文学に使うことができる.ミード湖の月ごとの平均水位について考察する:
アリゾナ州魚類鳥獣部よると,湖の最高水位レベルは1229フィートである:
特性と関係 (7)
KumaraswamyDistributionの特殊変換:
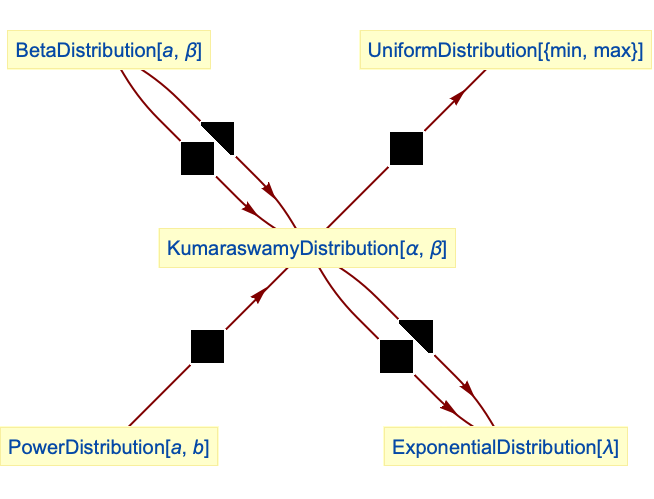
Kumaraswamy分布はBetaDistributionを変換したものである:
Kumarswamy分布を簡約するとBetaDistributionになる:
Kumaraswamy分布を簡約するとPowerDistributionになる:
UniformDistributionはKumaraswamyDistributionを変換したものである:
ExponentialDistributionは,Kumaraswamy分布を変換したものである:
テキスト
Wolfram Research (2010), KumaraswamyDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/KumaraswamyDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "KumaraswamyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/KumaraswamyDistribution.html.
APA
Wolfram Language. (2010). KumaraswamyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/KumaraswamyDistribution.html