LogisticDistribution
LogisticDistribution[μ,β]
平均 μ,尺度母数 β のロジスティック分布を表す.
平均0,尺度母数1のロジスティック分布を表す.
詳細
- LogisticDistributionは双曲線正割平方分布としても知られている.
- ロジスティック分布における値
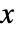 の確率密度は
の確率密度は 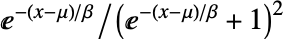 に比例する. »
に比例する. » - LogisticDistributionでは,μ は任意の実数,β は任意の正の実数でよい.
- LogisticDistributionでは,μ と β は単位次元が等しい任意の数量でよい. »
- LogisticDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- LogisticDistribution[μ,β]は,実数集合
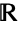 上で定義・サポートされ,実数 μ(分布の「平均」と呼ばれる)および正の実数 β(「尺度母数」と呼ばれる)でパラメータ化された連続統計分布を表す.ロジスティック分布の確率密度関数(PDF)は全体として単一の「峰」(最大値)を持つ単峰性であるが,その全体的な形は μ と β の形で決定される.加えて,ロジスティック分布のPDFの裾部は,PDFが
上で定義・サポートされ,実数 μ(分布の「平均」と呼ばれる)および正の実数 β(「尺度母数」と呼ばれる)でパラメータ化された連続統計分布を表す.ロジスティック分布の確率密度関数(PDF)は全体として単一の「峰」(最大値)を持つ単峰性であるが,その全体的な形は μ と β の形で決定される.加えて,ロジスティック分布のPDFの裾部は,PDFが 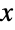 の大きい値について代数的というよりはむしろ指数的に減少するという意味で「薄い」(この動作は分布のSurvivalFunction を分析することで数量的に正確にできる).ロジスティック分布は,分布の累積分布関数(CDF)がロジスティック関数であるためにこのように命名されたもので,そのPDFが双曲線正割(Sech) 関数の二乗を連続的にかけたものとして実現出来ることから,双曲線正割二乗分布と呼ばれることがある.母数がない形のLogisticDistribution[]は LogisticDistribution[0,1]に等しく,「標準」ロジスティック分布と呼ばれることがある.
の大きい値について代数的というよりはむしろ指数的に減少するという意味で「薄い」(この動作は分布のSurvivalFunction を分析することで数量的に正確にできる).ロジスティック分布は,分布の累積分布関数(CDF)がロジスティック関数であるためにこのように命名されたもので,そのPDFが双曲線正割(Sech) 関数の二乗を連続的にかけたものとして実現出来ることから,双曲線正割二乗分布と呼ばれることがある.母数がない形のLogisticDistribution[]は LogisticDistribution[0,1]に等しく,「標準」ロジスティック分布と呼ばれることがある. - ロジスティックは,フランス人の数学者Pierre Verhulstによって,1830年代から1840年代にかけてはじめて研究され,ReedとBerksonによる1929年の論文でこの名前が付けられた.Verhulstの当初の興味は人口統計と人工のモデル化であった.ロジスティック分布は歴史的に統計学でいわゆるロジスティック回帰のツールとしてよく使われており,これもロジスティックの主な用法の一つであった.今日でも,ロジスティック分布は生存分析にしばしば利用され,左側打ち切りと右側打ち切りの両方のデータにフィットできることから,時間につれて失敗率が高くなる系のモデリングの際に,他の数量的に類似した分布(例:正規分布 (NormalDistribution))よりも好まれている.ロジスティック分布から導かれたツールやロジスティック分布に触発されたツールは,動物学や生理学を含むさまざまな生命科学で許容度データを表す際によく使われ,分布そのものも金融工学でさまざまな金融商品のリスクのモデル化に使われている.ロジスティック分布は,伝染病の広がり,セルの成長,改革の広がり等を含む多くの現象のモデル化に使うことができる.
- RandomVariateを使って,ロジスティック分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,LogisticDistribution[μ,β]] (より簡略な表記では xLogisticDistribution[μ,β] )を使って,確率変数 x がロジスティック分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- ロジスティック分布の確率密度関数および累積分布関数は,PDF[LogisticDistribution[μ,β] ,x]およびCDF[LogisticDistribution[μ,β] ,x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がロジスティック分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックロジスティック分布を推定することが,FindDistributionParametersを使ってデータをロジスティック分布にフィットすることができる.ProbabilityPlotを使って記号ロジスティック分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ロジスティック分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたロジスティック分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってロジスティック分布を含む高次元分布を構築することが,ProductDistributionを使ってロジスティック分布を含む独立成分分布の結合分布を計算することができる.
- LogisticDistributionは,他の多くの分布と関連がある.LogisticDistributionは,UniformDistributionとExponentialDistributionの両方の変換(TransformedDistribution)として実現することができ,ExponentialDistribution,GumbelDistribution,ExtremeValueDistributionのさまざまな線形結合から得ることができる.LogLogisticDistributionに従う確率変量
 の対数はLogisticDistributionでモデル化され,そのPDFの双曲線正割との関係から,LogisticDistributionはSechDistributionとも関係がある.LogisticDistributionは,GompertzMakehamDistribution,FrechetDistribution,ParetoDistribution,WeibullDistribution,MaxStableDistribution,MinStableDistributionとも関係がある.
の対数はLogisticDistributionでモデル化され,そのPDFの双曲線正割との関係から,LogisticDistributionはSechDistributionとも関係がある.LogisticDistributionは,GompertzMakehamDistribution,FrechetDistribution,ParetoDistribution,WeibullDistribution,MaxStableDistribution,MinStableDistributionとも関係がある.
例題
すべて開くすべて閉じるスコープ (7)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (2)
LogisticDistributionは前日終値からの僅かな株価変動に非常によくフィットする.スタンダード&プアーズ(Standard & Poor's)500種指数の2000年1月1日から2009年1月1日までの日々の変動の推定分布を求める:
ロジスティック分布を使うと従来のNormalDistributionを使うよりもよいフィットが得られる:
特性と関係 (11)
ロジスティック分布は平行移動と正の因子によるスケーリングの下では閉じている:
確率密度関数はSechの平方によって表すことができる:
ロジスティック分布はSechDistributionに似ている:
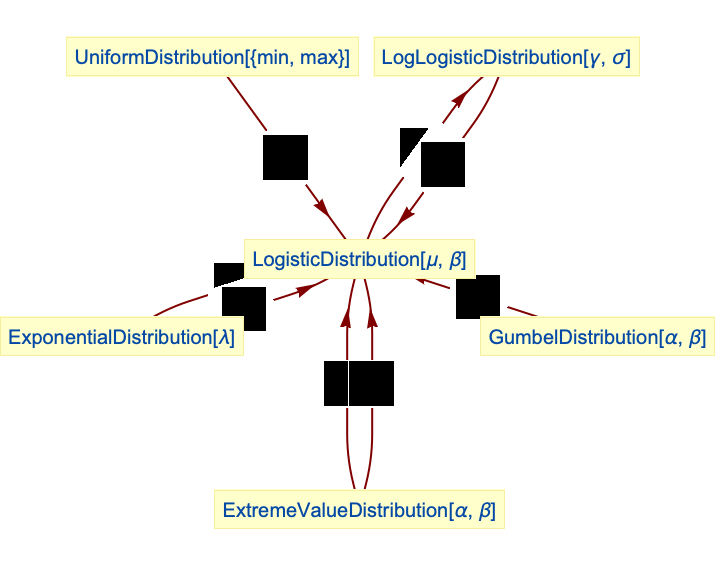
LogisticDistributionはLogLogisticDistributionに関連している:
ロジスティック分布はUniformDistributionを変換したものである:
ロジスティックはExponentialDistributionから変換したものである:
ロジスティックはExponentialDistributionを変換したものである:
GumbelDistributionに従う2つの変数の差はExtremeValueDistributionに従う2つの変数の差が従う分布,すなわちロジスティック分布に従う:
ExtremeValueDistributionとGumbelDistributionの和はロジスティック分布に従う:
ロジスティック分布は,ExtremeValueDistributionのParameterMixtureDistributionである:
考えられる問題 (2)
テキスト
Wolfram Research (2007), LogisticDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/LogisticDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "LogisticDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/LogisticDistribution.html.
APA
Wolfram Language. (2007). LogisticDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/LogisticDistribution.html