MeshConnectivityGraph
MeshConnectivityGraph[mr,0]
点が線で繋がれたグラフを与える.
MeshConnectivityGraph[mr,d]
次元 d-1のセルを共有する,次元 d のセルとセルの間のグラフを与える.
MeshConnectivityGraph[mr,{d,e},r]
次元 r のセルを共有する,次元 d のセルから次元 e のセルまでのグラフを与える.
詳細とオプション


- MeshConnectivityGraphはメッシュ隣接グラフおよびメッシュ接続グラフとしても知られている.
- 主な用途は,メッシュ中のセルの隣接情報と位相情報を得ることである.
- 連結度グラフの頂点{d,i}は,メッシュ mr 中の次元が d で指標が i のセル cd,iに対応する.
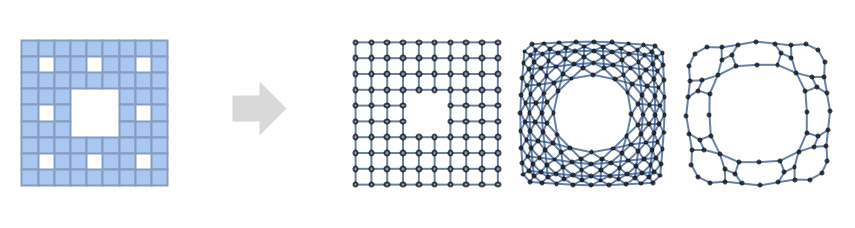
- MeshConnectivityGraph[mr,d]の無向辺は,セル cd,iとセル cd,jが両方とも次元 d-1の共通の部分セルを持つ場合は常に,2つの頂点{d,i}と{d,j}を繋ぐ.d=0については,共通の部分セルの次元は1である.
- 次は,d の一般的なケースである.
-
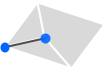
0 線を共有する点 
1 点を共有する線 
2 辺を共有する多角形 
3 多角形を共有する多面体 - MeshConnectivityGraph[mr,{d,e},r]では,セル cd,iとセル ce,jに cd,iと ce,jの部分集合あるいは上位集合である次元 r の共通のセルがある場合は常に,頂点{d,i}と頂点{e,j}が有向辺で繋がれる.
- MeshConnectivityGraph[mr]は事実上MeshConnectivityGraph[mr,0]に等しい.
- MeshConnectivityGraph[mr,d,r]はグラフMeshConnectivityGraph[mr,{d,d},r]の無向グラフに等しい.
- MeshConnectivityGraphはGraphと同じオプションに以下の変更を加えたものを取る.
-
AnnotationRules Inherited
全オプションのリスト

例題
すべて開くすべて閉じる例 (2)
スコープ (4)
MeshConnectivityGraphはMeshRegionに使うことができる:
MeshConnectivityGraphは全次元に使うことができる:
デフォルトで,AnnotationRulesInheritedの注釈は保持される:
AnnotationRulesNoneの設定のときは,注釈は保持されずグラフには指標が付けられる:
オプション (81)
AnnotationRules (4)
DirectedEdges (1)
デフォルトで,次元が異なるセルの間の連結度を計算するときは有向経路が生成される:
DirectedEdges->Falseを使って規則を無向辺として解釈する:
EdgeLabels (7)
Placedを記号位置と一緒に使って辺に沿ったラベルの置き方を制御する:
TooltipおよびStatusAreaからの値によって,自動的にラベルを付ける:
EdgeShapeFunction (6)
EdgeShapeFunctionの組込み設定のリストを得る:
EdgeShapeFunctionはEdgeStyleと組み合せることができる:
EdgeShapeFunctionはEdgeStyleより優先順位が高い:
GraphHighlightStyle (2)
GraphLayout (5)
VertexCoordinatesはGraphLayout座標を無効にする:
レイアウトアルゴリズムを使って計算されたVertexCoordinatesを,AbsoluteOptionsを使って抽出する:
VertexCoordinates (2)
AbsoluteOptionsを使って結果の頂点座標を抽出する:
VertexLabels (13)
Placedを記号位置と一緒に使って外側位置を含むラベルの置き方を制御する:
すべてのラベルを頂点の右上コーナーに置き,ラベル内で座標を変える:
Placedに引数を使ってTooltipを含むフォーマットを制御する:
あるいは,StatusAreaを含むフォーマットを制御する:
VertexShape (5)
任意のGraphics,ImageあるいはGraphics3Dを頂点の形として使う:
VertexShapeはVertexSizeと組み合せることができる:
VertexShapeはVertexStyleの影響は受けない:
VertexShapeFunctionはVertexShapeより優先順位が高い:
VertexShapeFunction (10)
VertexShapeFunctionの組込みコレクションのリストを得る:
"Basic"コレクション中のVertexShapeFunctionについての設定を使う:
"Rounded"コレクション中のVertexShapeFunctionについての組込み設定を使う:
"Concave"コレクション中のVertexShapeFunctionについての組込み設定を使う:
VertexShapeFunctionはVertexStyleと組み合せることができる:
VertexShapeFunctionはVertexStyleより優先順位が高い:
VertexShapeFunctionはVertexSizeと組み合せることができる:
VertexShapeFunctionはVertexShapeより優先順位が高い:
VertexSize (8)
VertexSizeはVertexShapeFunctionと組み合せることができる:
VertexSizeはVertexShapeと組み合せることができる:
VertexStyle (5)
VertexShapeFunctionはVertexStyleと組み合せることができる:
VertexShapeFunctionはVertexStyleより優先順位が高い:
VertexStyleはBaseStyleと組み合せることができる:
VertexStyleはBaseStyleより優先順位が高い:
VertexShapeはVertexStyleの影響は受けない:
アプリケーション (10)
基本的なアプリケーション (5)
多面体演算 (1)
MeshConnectivityGraphを使って立方体のDualPolyhedronを計算する:
位相演算 (3)
MeshConnectivityGraphを使ってメッシュが連結しているかどうかを調べる:
MeshConnectivityGraphを使ってConnectedMeshComponentsを計算する:
特性と関係 (3)
次元が異なるセル間のMeshConnectivityGraphは有向二部グラフである:
メッシュ連結度グラフの同じ次元のメッシュ間のAdjacencyMatrixは対称行列である:
テキスト
Wolfram Research (2020), MeshConnectivityGraph, Wolfram言語関数, https://reference.wolfram.com/language/ref/MeshConnectivityGraph.html.
CMS
Wolfram Language. 2020. "MeshConnectivityGraph." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MeshConnectivityGraph.html.
APA
Wolfram Language. (2020). MeshConnectivityGraph. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MeshConnectivityGraph.html