MultivariatePoissonDistribution

MultivariatePoissonDistribution[μ0,{μ1,μ2,…}]

平均ベクトル{μ0+μ1,μ0+μ2,…}の多変量ポアソン(Poisson)分布を表す．

詳細

  • 多変量ポアソン分布は{x0+x1,x0+x2,…}の分布に対応する．ただし，xiは平均 μiでポアソン分布に従う．
  • 母数 μiは任意の正の数でよい．
  • MultivariatePoissonDistributionは，Mean，CDF，RandomVariate等とともに使うことができる．

予備知識

  • MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}]は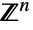，の部分集合上でサポートされ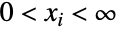，を満足する整数のすべてのタプル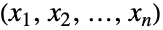からなり，各 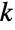番目の（一変量）周辺分布が 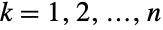についてPoissonDistributionであるという特性で特徴付けられる多変量離散統計分布を表す．表現を変えるなら，変数 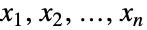のそれぞれが 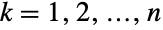について xkPoissonDistribution[μ0+μk]を満足する．多変量ポアソン分布は生の実数 μ0および実数ベクトル{μ1,μ2,…,μn} でパラメータ化される．これらは分布の合併平均，合併分散，合併共分散を定義する．多変量ポアソン分布は離散的で単峰性の確率密度関数(PDF)を持つ．
  • 多変量ポアソン分布をこれと類似した名前の多重ポアソン分布と区別する必要がある．後者は1950年代の終り頃研究の中心となり，それ自身の一変量周辺分布との組み合せとして特徴付けられている（これに比べ，MultivariatePoissonDistributionはその一変量周辺分布の積である）．
  • 多変量ポアソン分布の研究は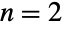，の特殊ケース（いわゆる二変量ポアソン分布）について1930年代に始まった．一般的な多変量のケースについての研究は1950年代に始まった．MultinormalDistributionのような他の多変量分布とは異なり，多変量ポアソン分布は数回再定義されている．再定義の多くには一般的にも専門家からの評価の面でも賛否両論があった．再定義の最も標準的なものでは，（ここで実装されているような）多変量ポアソン分布は，一変量ポアソン分布の最も自然な多変量への拡張であるとみなされており，神経スパイクパターンの分析や分類で隠れマルコフモデルの代りとして使われている．
  • RandomVariateを使って，多変量ポアソン分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}]]（より簡略な表記では xMultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}]）を使って，確率変数 x が多変量ポアソン分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}],{x1,x2,…,xn}]およびCDF[MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}],{x1,x2,…,xn}]を使って得られる．平均，中央値，分散，共分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Covariance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合が多変量ポアソン分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータから多変量パラメトリックポアソン分布を推定することが，FindDistributionParametersを使ってデータを多変量ポアソン分布にフィットすることができる．ProbabilityPlotを使って多変量記号ポアソン分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って多変量記号ポアソン分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換された多変量ポアソン分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使って多変量ポアソン分布を含む高次元分布を構築することが，ProductDistributionを使って多変量ポアソン分布を含む独立成分分布の結合分布を計算することができる．
  • MultivariatePoissonDistributionは他の多くの分布と関連がある．MultivariatePoissonDistributionは，上記で説明したように，PoissonDistributionと関係がある．MultivariatePoissonDistributionの一次元周辺確率密度関数はそれぞれがPoissonDistributionを満足し，各多変量周辺分布はMultivariatePoissonDistributionの例である．MultivariatePoissonDistributionは，複雑な，しかし厳密な在り方でMultinomialDistributionの極限ケースであり，一変量PoissonDistributionとの関係からBinomialDistribution，PolyaAeppliDistribution，PoissonConsulDistributionとも関係がある．

例題

すべて開くすべて閉じる

例  (4)

確率質量関数：

累積分布関数：

平均と分散：

共分散行列：

スコープ  (8)

ポアソン分布から擬似乱数ベクトルのサンプルを生成する：

分布母数推定：

サンプルデータから分布母数を推定する：

適合度検定：

各成分の歪度は μ と mu_(i) に依存する：

各成分の尖度は μ と mu_(i) に依存する：

相関：

二変量ポアソン分布のさまざまな混合モーメント：

混合中心モーメント：

混合階乗モーメント：

混合キュムラント：

記号次数の閉形式：

ハザード関数：

周辺分布：

アプリケーション  (2)

臨床実験で，薬剤Aは10万人につき12人の割合で副作用があり，薬剤Bは10万人につき9人の割合で副作用があった．薬剤AあるいはBを単独で用いた場合には全く副作用がない人でも両方を併用した場合に副作用があった人が50万人につき1人の割合であった．ポアソンモデルを想定して1万人の母集団の副作用の分布を求める：

薬剤Aに対する副作用が最高で3，薬剤Bに対する副作用が最高で4である確率を求める：

ある大学のキャンパスがAとBの2都市に完全にまたがっている．キャンパスでは1日平均10件の交通事故が発生する．キャンパス外では都市Aで5件，都市Bでは10件の交通事故がある．2都市の交通事故件数の結合分布を求める：

確率密度関数：

それぞれの都市の平均事故数を求める：

両都市の合計事故数の平均を求める：

ある特定の日に都市Bよりも都市Aで多くの事故が発生する確率を求める：

ランダムサンプルを使って両都市合計で1日に少なくとも12件の事故が発生する確率を求める：

特性と関係  (4)

多変量ポアソン分布は加算の下で閉じている：

一次元の多変量ポアソン分布はPoissonDistributionである：

成分は母数の許容されるすべての値について相関している：

多変量ポアソン分布はその周辺分布の積として表すことはできない：

周辺分布を求める：

周辺分布のProductDistributionを求める：

共分散行列を比較する：

確率密度関数を比較する：

Wolfram Research (2010), MultivariatePoissonDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html.

テキスト

Wolfram Research (2010), MultivariatePoissonDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html.

CMS

Wolfram Language. 2010. "MultivariatePoissonDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html.

APA

Wolfram Language. (2010). MultivariatePoissonDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html

BibTeX

@misc{reference.wolfram_2024_multivariatepoissondistribution, author="Wolfram Research", title="{MultivariatePoissonDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_multivariatepoissondistribution, organization={Wolfram Research}, title={MultivariatePoissonDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html}, note=[Accessed: 18-November-2024 ]}