MultivariatePoissonDistribution
MultivariatePoissonDistribution[μ0,{μ1,μ2,…}]
表示均值向量为 {μ0+μ1,μ0+μ2,…} 的多元泊松分布.
更多信息
- 多元泊松分布对应于 {x0+x1,x0+x2,…} 的分布,其中 xi 为均值为 μi 的泊松分布.
- 参数 μi 可取任意正数.
- MultivariatePoissonDistribution 可与 Mean、CDF 以及 RandomVariate 等函数联合使用.
背景
- MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}] 表示一个支持在
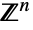 上的离散多变量统计分布,含有 满足
上的离散多变量统计分布,含有 满足 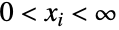 的整数构成的所有元组并且对于
的整数构成的所有元组并且对于 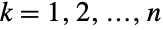 各个第
各个第 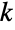 个(单变量)边际分布满足 PoissonDistribution. 换言之,对于
个(单变量)边际分布满足 PoissonDistribution. 换言之,对于 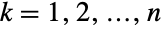 、
、 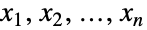 中的各个变量满足 xkPoissonDistribution[μ0+μk],对于
中的各个变量满足 xkPoissonDistribution[μ0+μk],对于 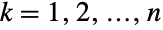 . 多变量泊松分布由正实数 μ0 和实数向量 {μ1,μ2,…,μn} 参数化,这些参数共同定义分布的相关均值、方差和协方差. 多变量泊松分布有离散的单峰概率密度函数(PDF).
. 多变量泊松分布由正实数 μ0 和实数向量 {μ1,μ2,…,μn} 参数化,这些参数共同定义分布的相关均值、方差和协方差. 多变量泊松分布有离散的单峰概率密度函数(PDF). - 需要特别注意的是多变量泊松分布和与之有相似名称的多重泊松分布之间的区别. 后者与1950年代后期成为研究的重点,并且以是其单变量边际的联合分布为特征.(与此相反,MultivariatePoissonDistribution 不是其单变量边际的积.)
- 关于多变量泊松分布的研究始于1930年代对
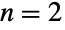 的特殊情况(所谓的双变量泊松分布)的研究,而对更普通的多变量情况的分析始于1950年代后期. 与其他如 MultinormalDistribution,多变量泊松分布被重定义过若干次,它的很多变形在获得接受的同时也引起了一些批判. 在其最标准的变形中,多变量(如在这里执行的)泊松分布被认为是单变量泊松分布的最自然的多变量延伸并且在对神经突起模式的分析和分类中作为隐藏 Markov 模型的替代应用.
的特殊情况(所谓的双变量泊松分布)的研究,而对更普通的多变量情况的分析始于1950年代后期. 与其他如 MultinormalDistribution,多变量泊松分布被重定义过若干次,它的很多变形在获得接受的同时也引起了一些批判. 在其最标准的变形中,多变量(如在这里执行的)泊松分布被认为是单变量泊松分布的最自然的多变量延伸并且在对神经突起模式的分析和分类中作为隐藏 Markov 模型的替代应用. - RandomVariate 可用于从一个多变量泊松分布中给出一个或多个机器精度或任意精度(后者通过 WorkingPrecision 选项)伪随机变量. Distributed[x,MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}]],更简洁地写作 xMultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}],可用于断言一个随机变量 x 符合多变量泊松分布. 这样的断言可用于如 Probability、 NProbability、 Expectation 和 NExpectation 等函数.
- 多变量泊松分布的概率密度和累积分布函数可以通过 PDF[MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}],{x1,x2,…,xn}] 和 CDF[MultivariatePoissonDistribution[μ0,{μ1,μ2,…,μn}],{x1,x2,…,xn}] 给出. 均值、中位数、方差、协方差、原始矩和中心矩可以分别通过 Mean、 Median、 Variance、 Covariance、 Moment 和 CentralMoment 计算出.
- DistributionFitTest 可用于测试给定数据集是否符合多变量泊松分布, EstimatedDistribution 可用于从给定数据中估计一个多变量泊松参数化分布,而 FindDistributionParameters 可用于拟合数据至一个多变量泊松分布. ProbabilityPlot 可用于生成一个给定数据的 CDF 对符号化多变量泊松分布的 CDF 的图像,而 QuantilePlot 可用于生成给定数据的分位数对符号化多变量泊松分布的分位数的图像.
- TransformedDistribution 可用于表示一个变形的多变量泊松分布,CensoredDistribution 可用于表示一个上限和下限之间的删节值的分布,而 TruncatedDistribution 可用于表示一个上限和下限之间的截尾值的分布. CopulaDistribution 可用于构建包含多变量泊松分布的更高维的分布,而 ProductDistribution 可用于计算涉及多变量泊松分布的有独立组分分布的联合分布.
- MultivariatePoissonDistribution 和许多其他统计分布有关. 如上所述, MultivariatePoissonDistribution 与 PoissonDistribution 有关,虽然每个 MultivariatePoissonDistribution 的一维边缘 PDF 都满足 PoissonDistribution,但是每个多变量边缘 PDF 仍然是 MultivariatePoissonDistribution 的实例. 复杂但精确,MultivariatePoissonDistribution 是 MultinomialDistribution 的极限特例,而且,因为与单变量 PoissonDistribution 的关系,MultivariatePoissonDistribution 还与 BinomialDistribution、PolyaAeppliDistribution 和 PoissonConsulDistribution 有关.
范例
打开所有单元关闭所有单元范围 (8)
应用 (2)
在临床研究中,药物 A 在平均情况下,每10万人有12个人会产生不良反应,而药物 B 每10万人有 9 个人会产生不良反应. 研究发现,虽然有些人对单独使用 A 或 B 不产生不良反应,但是两者混合平均会使50万人有1人产生不良反应. 假定这是一个泊松模型,求1万人中不良反应的分布:
求对药物 A 至多有3个不良反应,对药物 B 至多有 4 个不良反应的概率:
一个大学校园完全位于两个双城 A 和 B 中. 平均来说,在一天里,校园内发生 10 起交通事故;除了校园以外,A 城内发生其它 5 起事故,B 城内发生其它 10 起事故. 求在双城中发生的事故数目的联合分布:
属性和关系 (4)
一维多变量泊松分布是 PoissonDistribution:
求边缘分布的 ProductDistribution:
文本
Wolfram Research (2010),MultivariatePoissonDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html.
CMS
Wolfram 语言. 2010. "MultivariatePoissonDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html.
APA
Wolfram 语言. (2010). MultivariatePoissonDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/MultivariatePoissonDistribution.html 年