NContourIntegrate

NContourIntegrate[f,z∈cont]

複素平面上で cont で定義される曲線に沿った f の数値積分を与える．

詳細とオプション

  • 周回積分は経路積分あるいは複素線積分としても知られている．
  • 周回積分は複素解析における正則関数および有理型関数の研究で発現したものであるが，現在では逆ラプラス(Laplace)変換およびZ変換の計算，定積分と総和，偏微分方程式の解を含む幅広い分野で使われている．
  • 積分路 cont 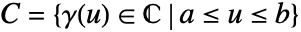に沿った関数 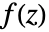の周回積分は以下で与えられる．
  • 周回積分の値はパラメータ化には依存しないが，積分路 cont の向きには依存する．
  • 関数 f は，通常は z の有理型関数であるが，複素平面内の cont の近傍で定義される任意の区分連続関数でよい．
  • 有理型関数 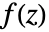の閉じた積分路 cont に沿った周回積分はコーシー(Cauchy)の留数定理を使って計算できる．
  • 次は，よく使われる閉じた積分路 cont である． »
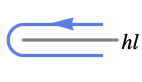
  • {"Hairpin",hl}半直線 hl を囲む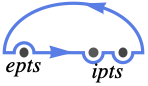
    {"UpperSemicircle",ipts,epts}すべて実軸上の点 ipts を含み点 epts は含まない上半平面を囲む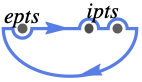
    {"LowerSemicircle",ipts,epts}すべて実軸上の点 ipts を含み点 epts は含まない下半平面を囲む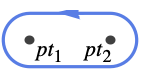
    {"Dumbbell",pt1,pt2}点 pt1と点 pt2で与えられるカプセルを囲む
  • 複素点は{x,y}のペアで与えられる．複素半直線はHalfLineプリミティブとして与えられる．
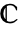  • における積分路 cont は 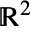における曲線領域(RegionQ)としても指定できる．
  • パラメトリック積分路ParametricRegion[{x[t],y[t]},{{t,a,b}}]の向きは t が増加する方向である．
  • 次は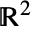，における特殊積分路とその推定される方向である．
  • Line[{p1,p2,…}]p1から p2まで等
    HalfLine[{p1,p1}]p1から p2に向かう
    InfiniteLine[{p1,p2}]p1から p2に向かう
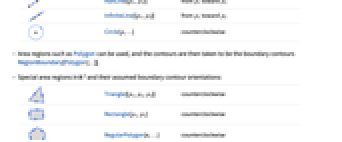
    Circle[p,…]反時計回り
  • Polygonのような面領域を使うことができる．その場合の積分路は境界線RegionBoundary[Polygon[…]]である．
  • 次は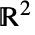，における特殊面領域とその推定境界線の向きである．
  • Triangle[{p1,p2,p3}]反時計回り
    Rectangle[p1,p2]反時計回り
    RegularPolygon[n,…]反時計回り
    Polygon[{p1,p2,…}{{q1,q2,…},…}]外側の積分路の反時計回り，内側の積分路の時計回り
    Disk[p,…]反時計回り
    Ellipsoid[p,…]反時計回り
    StadiumShape[{p1,p2},r]反時計回り
    Annulus[p,{rm,rm},…]外側の積分路の反時計回り，内側の積分路の時計回り
  • cont 内の領域は，自動評価を避けるためにInactiveでラップされることがある．
  • 次は，使用可能なオプションである．
  • AccuracyGoal Automatic目標絶対確度の桁数
    MaxPoints Automaticサンプル点の最大総数
    MaxRecursion Automatic再帰的下位区分の最大数
    Method Automatic使用するメソッド
    MinRecursion 0再帰的下位区分の最小数
    PrecisionGoal Automatic目標精度の桁数
    WorkingPrecision Automatic内部計算精度

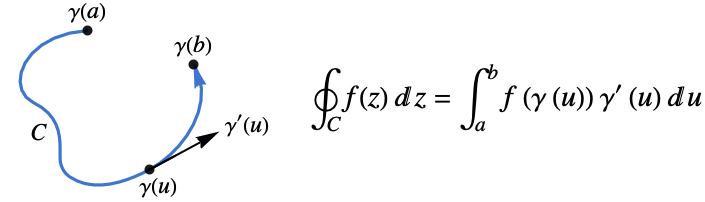
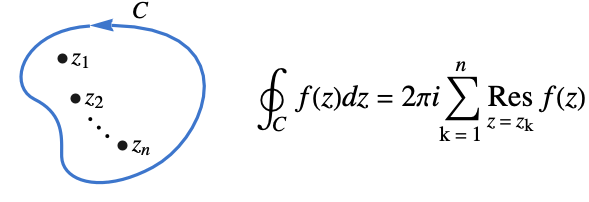
例題

すべて開くすべて閉じる

例  (3)

単位円に沿って1/z を積分する：

中心が原点で半径2の円に沿って有理関数を積分する：

楕円の輪郭に沿って有理型関数を積分する：

結果をContourIntegrateと比較する：

スコープ  (46)

基本的な用法  (9)

円形経路上の周回積分：

ContourIntegrateと比較する：

複素平面の折れ線上の周回積分：

半円板上の周回積分：

三角関数の式の数値周回積分：

複素平面のパラメトリック輪郭上の周回積分：

閉じた半円上の有理型関数の周回積分：

真性特異点を持つ関数の周回積分：

非解析的関数の周回積分：

分枝切断線を持つ関数の周回積分：

スペシャルトピック：有理関数  (8)

円に沿って有理関数を積分する：

正五角形の輪郭に沿って有理関数を積分する：

三角形の経路に沿った有理関数の周回積分：

矩形の経路に沿った有理関数の周回積分：

単位円に沿った周回積分：

開いた折れ線上の周回積分：

開いた円弧の上の周回積分：

円形経路に沿った有理関数の周回積分：

スペシャルトピック：有理型関数  (5)

多角形経路に沿った有理型関数の周回積分：

周回積分を記号的に評価する：

楕円経路に沿った周回積分：

閉じた半円上の周回積分：

アニュラスの扇形上の周回積分：

半径6の円の上の周回積分：

スペシャルトピック：真性特異点を持つ関数  (4)

指数関数：

輪郭内に真性特異点があるSin関数：

真性特異点がある関数の周回積分：

周期関数から生起する真性特異点：

スペシャルトピック：非解析的関数  (4)

円形経路上の周回積分：

Arg関数の周回積分：

楕円の扇形上の周回積分：

矩形経路上の周回積分：

スペシャルトピック：分枝切断線がある関数  (2)

区分連続関数の周回積分：

積分経路上に分枝切断線がある関数の周回積分：

スペシャルトピック：名前付きの積分路  (7)

複素平面の上半分で閉じている，実軸上の極の周りの，正の方向の実軸に沿った周回積分：

2つ目の例：

複素平面の下半分で閉じている，実軸上の極の周りの，正の方向の実軸に沿った周回積分：

デフォルトで，この積分路は時計回りに進む．

2つ目の例：

ヘアピン積分路あるいはハンケル(Hankel)積分路の周りの周回積分：

ヘアピン積分路あるいはハンケル積分路の周りの積分：

記号評価と比較する：

評価するとZeta関数になる周回積分：

数値評価：

ヘアピン積分路またはハンケル積分路：

0と1を繋ぐ分枝切断線の周りのDumbbell積分路：

スペシャルトピック：領域の輪郭  (7)

無限直線上の周回積分：

円形の輪郭上の周回積分：

線分上の周回積分：

三角経路上の周回積分：

矩形経路上の周回積分：

扇形上の周回積分：

アニュラス上の周回積分：

オプション  (7)

AccuracyGoal  (1)

オプションAccuracyGoalは確度の桁数を設定する：

デフォルト設定による結果はPrecisionGoalしか設定しない：

MaxPoints  (1)

オプションMaxPointsは，指定された数の点の評価をした後で積分を中止する：

MaxRecursion  (1)

オプションMinRecursionは再帰ステップの最大数を指定する：

再帰回数を増やす：

厳密結果は以下のようになる：

Method  (1)

オプションMethodはNIntegrateにおけるのと同じ値を取ることができる．例として以下を見よ：

デフォルトオプションでは以下のようになる：

切り取られた厳密結果と比較する：

MinRecursion  (1)

オプションMinRecursionは下位区分が最小数になるように強制する：

厳密な結果と比較する：

PrecisionGoal  (1)

オプションPrecisionGoalは積分の相対許容度を設定する：

デフォルト設定では以下のようになる：

WorkingPrecision  (1)

WorkingPrecisionを使って作業精度が設定できる：

アプリケーション  (22)

有理関数  (2)

大きい半径の半円板の周回積分：

これは，記号的に計算された大きい についての極限と一致する：

NIntegrateによって入手した同じ結果：

実線上の積分：

これは，周回積分の極限として得ることができる：

三角関数と有理関数の積  (2)

実線上の積分：

これら2つの結果は，大きい半径の半円板に沿った複素積分を使って回復することができる：

実線上の積分：

複素積分を使う：

三角関数  (3)

正弦の有理関数の積分：

これは，周回積分として回復することができる：

余弦の有理関数の積分：

これは，周回積分として入手できる：

正弦の有理関数の積分：

周回積分として：

フーリエ変換  (2)

関数のフーリエ(Fourier)変換：

正の について：

数値周回積分を使った計算：

負の について：

関数のフーリエ変換：

正の についての周回積分を使った計算：

負の について：

逆ラプラス変換  (4)

関数の逆ラプラス変換：

について：

周回積分を使った計算：

有理関数の対数の逆ラプラス変換：

について：

周回積分を使う：

平方根を含む関数の逆ラプラス変換：

について：

周回積分を使った同じ計算：

Logを含む関数の逆ラプラス変換：

について：

逆ラプラス変換の定義を使う：

逆メリン変換  (4)

関数の逆メリン(Mellin)変換：

について：

周回積分でこれを計算する：

関数の逆メリン変換：

について：

周回積分としての定義でこれを計算する：

関数のメリン変換：

逆メリン変換を使って における関数を回復する：

これは以下に等しい：

有理関数のメリン変換：

における関数を逆メリン変換を使って回復する：

逆Z変換  (2)

関数の逆Z変換：

について：

結果を周回積分としての定義から入手する：

関数の逆Z変換：

について：

大きい半径の周回積分としての定義から：

古典的な定理  (3)

閉じた経路上で有理型関数の周回積分に適用された留数定理：

この積分は， 掛ける輪郭内の極の留数の和に等しい：

積分の等高線は，関数の特異値を横切らなければ，積分の値を変えずに変形することができる：

等高線内に特異値がない場合，積分は0である：

特性と関係  (6)

記号計算ができなければ，N[ContourIntegrate[…]]を適用して数値解を得る：

これは，NIntegrateを使って計算することもできる：

これは，NContourIntegrateで計算することもできる：

数値周回積分は，NIntegrateを使って得ることもできる：

これは以下に等しい：

NIntegrateは複素平面上の真っ直ぐな等高線に沿って積分する：

これは以下に等しい：

閉じた経路上の周回積分はResidueSumで得ることもできる：

有理型関数の曲はFunctionPolesで求められる：

この積分はResidueで計算することもできる：

閉じた経路上の周回積分はResidueで求めることもできる：

インタラクティブな例題  (2)

さまざまな半径の扇形上の周回積分：

ContourIntegrateと比較する：

さまざまな半径の扇形上の別の周回積分：

ContourIntegrateと比較する：

Wolfram Research (2024), NContourIntegrate, Wolfram言語関数， https://reference.wolfram.com/language/ref/NContourIntegrate.html.

テキスト

Wolfram Research (2024), NContourIntegrate, Wolfram言語関数， https://reference.wolfram.com/language/ref/NContourIntegrate.html.

CMS

Wolfram Language. 2024. "NContourIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/NContourIntegrate.html.

APA

Wolfram Language. (2024). NContourIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NContourIntegrate.html

BibTeX

@misc{reference.wolfram_2024_ncontourintegrate, author="Wolfram Research", title="{NContourIntegrate}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NContourIntegrate.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ncontourintegrate, organization={Wolfram Research}, title={NContourIntegrate}, year={2024}, url={https://reference.wolfram.com/language/ref/NContourIntegrate.html}, note=[Accessed: 22-November-2024 ]}