NContourIntegrate

NContourIntegrate[f,z∈cont]

给出 f 在复平面中由 cont 定义的环线上的数值积分.

更多信息和选项

  • 围道积分也称为路径积分或复线积分.
  • 围道积分出现在复分析中对全纯和亚纯函数的研究中，但现在它们的应用范围很广，包括计算拉普拉斯逆变换和 Z 变换、定积分与和，以及偏微分方程的解.
  • 函数 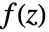沿环线 cont 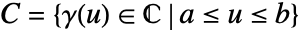的围道积分由下式给出：
  • 围道积分的值与参数化无关，但与环线 cont 的方向有关.
  • 函数 f 通常是 z 的亚纯函数，但它可以是在复平面中 cont 邻域中定义的任意分段连续函数.
  • 可使用柯西留数定理计算亚纯函数 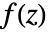沿闭合环线 cont 的围道积分.
  • 常用的闭合环线 cont 包括： »
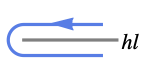
  • {"Hairpin",hl}包围半直线 hl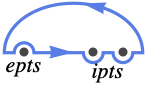
    {"UpperSemicircle",ipts,epts}包围上半平面，包括点 ipts，不包括点 epts，全部在实轴上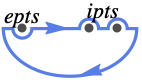
    {"LowerSemicircle",ipts,epts}包围下半平面，包括点 ipts，不包括点 epts，全部在实轴上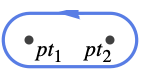
    {"Dumbbell",pt1,pt2}包围由点 pt1 和 pt2 给定的胶囊
  • 复数点以 {x,y} 数据对的形式给出；复半直线以 HalfLine 基元的形式给出.
  • 也可以用 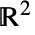中的曲线区域 (RegionQ) 指定 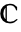中的环线 cont.
  • 对于参数化环线 ParametricRegion[{x[t],y[t]},{{t,a,b}}]，方向是 t 增大的方向.
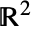  • 中的特殊环线及认定的方向：
  • Line[{p1,p2,…}]从 p1 到 p2 等
    HalfLine[{p1,p1}]从 p1 到 p2
    InfiniteLine[{p1,p2}]从 p1 到 p2
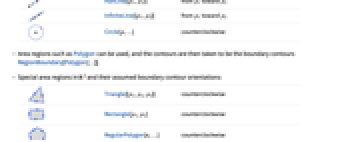
    Circle[p,…]逆时针
  • 可以使用诸如 Polygon 之类的面区域，然后将环线视为边界环线 RegionBoundary[Polygon[…]].
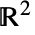  • 中的特殊面区域及认定的边界环线的方向：
  • Triangle[{p1,p2,p3}]逆时针
    Rectangle[p1,p2]逆时针
    RegularPolygon[n,…]逆时针
    Polygon[{p1,p2,…}{{q1,q2,…},…}]外部环线采用逆时针方向，内部环线采用顺时针方向
    Disk[p,…]逆时针
    Ellipsoid[p,…]逆时针
    StadiumShape[{p1,p2},r]逆时针
    Annulus[p,{rm,rm},…]外部环线采用逆时针方向，内部环线采用顺时针方向
  • cont 中的区域可能被 Inactive 封装，以避免自动计算.
  • 可给出以下选项：
  • AccuracyGoal Automatic寻求的绝对准确度
    MaxPoints Automatic样本点的最大数量
    MaxRecursion Automatic递归子划分的最大数量
    Method Automatic要使用的方法
    MinRecursion 0递归子划分的最小数量
    PrecisionGoal Automatic寻求的精度
    WorkingPrecision Automatic内部计算使用的精度

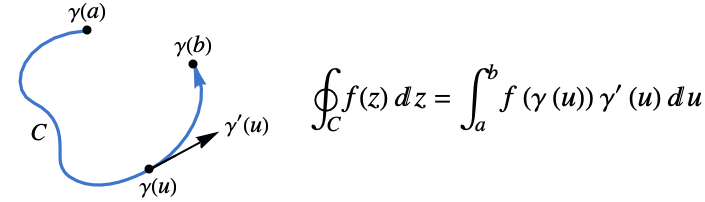
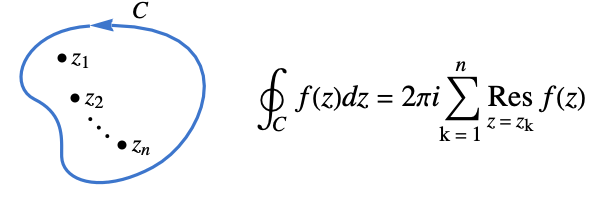
范例

打开所有单元关闭所有单元

基本范例  (3)

沿单位圆对 1/z 进行积分：

沿以原点为圆心、半径为 2 的圆对有理函数进行积分：

沿椭圆环线对亚纯函数进行积分：

与 ContourIntegrate 的结果相比较：

范围  (46)

基本用法  (9)

圆形路径上的围道积分：

与 ContourIntegrate 相比较：

复平面中多边形链上的围道积分：

半圆盘上的围道积分：

三角表达式的数值围道积分：

复平面中参数化环线上的围道积分：

亚纯函数在闭合半圆上的围道积分：

具有本质奇点的函数的围道积分：

非解析函数的围道积分：

包含分支切割的函数的围道积分：

特殊主题：有理函数  (8)

沿圆对有理函数进行积分：

沿五边形环线对有理函数进行积分：

有理函数沿三角形路径的围道积分：

有理函数沿矩形路径的围道积分：

沿单位圆的围道积分：

开放多边形链上的围道积分：

开放弧线上的围道积分：

有理函数沿圆形路径的围道积分：

特殊主题：亚纯函数  (5)

亚纯函数沿多边形路径的围道积分：

符号式计算围道积分：

沿椭圆路径的围道积分：

闭合半圆上的围道积分：

部分圆环上的围道积分：

半径为 6 的圆上的围道积分：

特殊主题：含有本质奇点的函数  (4)

指数函数：

环线内有本质奇点的 Sin 函数：

具有本质奇点的函数的围道积分：

由周期函数产生的本质奇点：

特殊主题：非解析函数  (4)

圆形路径上的围道积分：

Arg 函数的围道积分：

椭圆扇形上的围道积分：

矩形路径上的围道积分：

特殊主题：有分支切割的函数  (2)

分段连续函数的围道积分：

在积分路径上有分支切割的函数的围道积分：

特殊主题：已命名的环线  (7)

沿实轴正方向、围绕实轴上的极点、闭合于复平面上半部分的围道积分：

第二个例子：

沿实轴正方向、围绕实轴上的极点、闭合于复平面下半部分的围道积分：

默认情况下，该环线被顺时针遍历.

第二个例子：

绕发夹形环线或 Hankel 环线的围道积分：

绕发夹形环线或 Hankel 环线的积分：

与符号计算的结果相比较：

计算结果为 Zeta 函数的围道积分：

用数值法计算：

发夹形环线或 Hankel 环线：

环绕分支切割的哑铃形环线，连接 0 和 1：

特殊主题：区域环线  (7)

无限直线上的围道积分：

圆形环线上的围道积分：

线段上的围道积分：

三角形路径上的围道积分：

矩形路径上的围道积分：

扇形上的围道积分：

圆环上的围道积分：

选项  (7)

AccuracyGoal  (1)

选项 AccuracyGoal 设置准确度的位数：

默认设置仅设定 PrecisionGoal：

MaxPoints  (1)

选项 MaxPoints 在计算指定数量的点后停止积分：

MaxRecursion  (1)

选项 MaxRecursion 指定最大递归步骤数：

增大递归计算的次数：

精确结果为：

Method  (1)

选项 Method 可接受与 NIntegrate 同样的值. 例如：

使用默认选项：

与截断的精确结果进行比较：

MinRecursion  (1)

选项 MinRecursion 强制使用最小数量的递归子划分：

与精确结果进行比较：

PrecisionGoal  (1)

选项 PrecisionGoal 设置积分中的相对容差：

使用默认设置：

WorkingPrecision  (1)

可用 WorkingPrecision 设置工作精度：

应用  (22)

有理函数  (2)

大半径半圆盘上的围道积分：

它与符号计算时 的极限一致：

用 NIntegrate 可获得同样的结果：

实轴上的积分：

也可以用围道积分的极限获取同样的结果：

三角函数与有理函数的积  (2)

实轴上的积分：

这两个结果也可以使用沿大半径半圆的复积分来获得：

实轴上的积分：

使用复积分：

三角函数  (3)

正弦有理函数的积分：

也可以使用围道积分来计算：

余弦有理函数的积分：

也可以使用围道积分来计算：

正弦有理函数的积分：

围道积分：

傅立叶变换  (2)

函数的傅立叶变换：

对于正的 ：

用数值围道积分进行计算：

对于负的 ：

函数的傅立叶变换：

用围道积分进行计算：对于正的 ：

对于负的 ：

拉普拉斯逆变换  (4)

函数的拉普拉斯逆变换：

对于 ：

用围道积分计算：

有理函数的对数的拉普拉斯逆变换：

对于 ：

使用围道积分：

含有平方根的函数的拉普拉斯逆变换：

对于 ：

用围道积分进行相同的计算：

含有 Log 的函数的拉普拉斯逆变换：

对于 ：

使用拉普拉斯逆变换的定义：

梅林逆变换  (4)

函数的梅林逆变换：

对于 ：

用围道积分计算：

函数的梅林逆变换：

对于 ：

根据围道积分的定义计算：

函数的梅林变换：

用梅林逆变换恢复 处的函数：

与下面的结果一致：

有理函数的梅林变换：

用梅林逆变换恢复 处的函数：

Z 逆变换  (2)

函数的 Z 逆变换：

对于 ：

根据围道积分的定义获取结果：

函数的 Z 逆变换：

对于 ：

根据大半径围道积分的定义：

经典定理  (3)

将留数定理应用于亚纯函数在闭合路径上的围道积分：

积分等于 乘以环线内极点的留数之和：

积分环线可以在不改变积分值的情况下改变形状，前提是没有与函数的奇异点相交：

如果环线内没有奇点，则积分为零：

属性和关系  (6)

如果符号计算失败，可用 N[ContourIntegrate[…]] 获得数值解：

也可用 NIntegrate 进行计算：

也可用 NContourIntegrate 进行计算：

用 NIntegrate 也可以计算数值围道积分：

这相当于：

NIntegrate 可以沿复平面中的直线进行积分：

这相当于：

也可以使用 ResidueSum 获得闭合路径上的围道积分：

可以使用 FunctionPoles 找到亚纯函数的极点：

也可以使用 Residue 计算积分：

也可以使用 Residue 获得闭合路径上的围道积分：

互动范例  (2)

不同半径的扇形上的围道积分：

与 ContourIntegrate 相比较：

另一个不同半径的扇形上的围道积分：

与 ContourIntegrate 相比较：

Wolfram Research (2024)，NContourIntegrate，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NContourIntegrate.html.

文本

Wolfram Research (2024)，NContourIntegrate，Wolfram 语言函数，https://reference.wolfram.com/language/ref/NContourIntegrate.html.

CMS

Wolfram 语言. 2024. "NContourIntegrate." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/NContourIntegrate.html.

APA

Wolfram 语言. (2024). NContourIntegrate. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NContourIntegrate.html 年

BibTeX

@misc{reference.wolfram_2024_ncontourintegrate, author="Wolfram Research", title="{NContourIntegrate}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/NContourIntegrate.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ncontourintegrate, organization={Wolfram Research}, title={NContourIntegrate}, year={2024}, url={https://reference.wolfram.com/language/ref/NContourIntegrate.html}, note=[Accessed: 22-November-2024 ]}