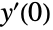NDSolve[eqns,u,{x,xmin,xmax}]
xminから xmaxの範囲における独立変数 x の関数 u について,常微分方程式 eqns の数値解を求める.
NDSolve[eqns,u,{x,xmin,xmax},{y,ymin,ymax}]
偏微分方程式 eqns を矩形領域上で解く.
NDSolve[eqns,u,{x,y}∈Ω]
偏微分方程式 eqns を,領域 Ω 上で解く.
NDSolve[eqns,u,{t,tmin,tmax},{x,y}∈Ω]
時間依存偏微分方程式 eqns を,領域 Ω 上で解く.
NDSolve[eqns,{u1,u2,…},…]
関数 uiを解く.






NDSolve
NDSolve[eqns,u,{x,xmin,xmax}]
xminから xmaxの範囲における独立変数 x の関数 u について,常微分方程式 eqns の数値解を求める.
NDSolve[eqns,u,{x,xmin,xmax},{y,ymin,ymax}]
偏微分方程式 eqns を矩形領域上で解く.
NDSolve[eqns,u,{x,y}∈Ω]
偏微分方程式 eqns を,領域 Ω 上で解く.
NDSolve[eqns,u,{t,tmin,tmax},{x,y}∈Ω]
時間依存偏微分方程式 eqns を,領域 Ω 上で解く.
NDSolve[eqns,{u1,u2,…},…]
関数 uiを解く.
詳細とオプション








- NDSolveは,結果をInterpolatingFunctionオブジェクトで与える数値微分方程式ソルバである.
- NDSolve[eqns,u[x],{x,xmin,xmax}]は,関数 u 自体の解を与える代りに u[x]の解を与える.
- 微分方程式は,Dtで得られる全微分商ではなく,Dで得られる u'[x]のような導関数で記述しなければならない.
- 偏微分方程式は,微分演算子のGrad (∇),Div (∇.),Laplacian (∇2),Curl (∇)を使って指定することもできる.一般に,これらの演算子は,演算子形が評価されるのを防ぐために,Inactive[op]で使われる.
- NDSolveは,多種の常微分方程式と多くの偏微分方程式を解くことができる.
- NDSolveは,多くの遅延微分方程式も解くことができる.
- 常微分方程式では,関数 uiは単一変数 t だけに依存するものとする.偏微分方程式では,複数の変数に依存してもよい.
- WhenEvent[event,action]を方程式 eqns に入れて event がTrueになったときに実現する action を指定することができる.
- uiの完全解を得るには,十分な初期条件または境界条件を微分方程式に与えておかなければならない.
- 初期条件と境界条件は,通常 u[x0]==c0, u'[x0]==dc0のように与える.実際に与える式はより複雑なものであっても構わない.
- c0,dc0等は,u[x]がベクトルあるいは一般的なリストの値を持つ関数であることを指定するリストでもよい.
- 周期境界条件は u[x0]==u[x1]を用いて指定することができる.
- 初期条件や境界条件に現れる点 x0は,解を求める xminから xmaxの範囲に必ずしもなくてよい.
- 境界値もまたDirichletConditionおよびNeumannValue.を使って指定することができる.
- 遅延微分方程式では,最初の履歴関数が u[x/;x<x0]==c0の形式で与えられる.ただし,c0は一般に x の関数である.
- NDSolveの微分方程式には,複素数を使うことができる.
- NDSolveは多くの微分代数方程式を解くことができる.この場合,eqns が純粋に代数的なこともあれば,変数のあるものが陰的に代数的なこともある.
- uiは従属変数の関数であり得るが,そのような変数すべてを含んでいる必要はない.
- 指定可能なオプション
-
AccuracyGoal Automatic 目標とする絶対確度の桁数 Compiled Automatic 式を自動的にコンパイルするかどうか DependentVariables Automatic 全従属変数のリスト EvaluationMonitor None 関数が評価されたときに常に評価される式 InitialSeeding {} いくつかのアルゴリズムのためのシード方程式 InterpolationOrder Automatic 最終出力の連続性の程度 MaxStepFraction 1/10 各ステップでカバーする領域の最大割合 MaxSteps Automatic 最大ステップ数 MaxStepSize Automatic 各ステップの最大刻み幅 Method Automatic 使用されるアルゴリズム NormFunction Automatic 誤差推定に用いるノルム PrecisionGoal Automatic 目標とする精度の桁数 StartingStepSize Automatic 使用する最初の刻み幅 StepMonitor None ステップを取る際に評価される式 WorkingPrecision MachinePrecision 内部計算で使用する精度 - NDSolveは解における推定誤差がPrecisionGoalとAccuracyGoalで指定された許容率内に収まるような刻み幅を取る.
- オプションNormFunction->f は各 uiの推定誤差を f[{e1,e2,…}]を用いて統合するように指定する.
- AccuracyGoalは,実質的に解を求める各ステップで許される絶対的な局所誤差を指定し,PrecisionGoalは相対的な局所誤差を指定する.
- 解がゼロ近傍にあるときに,解が正確に求められなければならない場合は,AccuracyGoalを大き目に設定するか,Infinityに設定するとよい.
- AccuracyGoalやPrecisionGoalのデフォルト値のAutomaticはWorkingPrecision/2に等しい.
- MaxStepsのデフォルト設定Automaticは,開始時および終了時と推定されるステップサイズによるNDSolveの最大ステップ数を推定している.これが不可能な場合には,固定ステップ数が使われる.
- MaxStepFractionの設定で各独立変数の値の幅の割合としてNDSolveの最大刻み幅を指定する.
- DependentVariables->Automaticの場合,NDSolveは与えられた方程式を解析して従属変数を決定しようとする.
- NDSolveは一般に微分方程式を,その方程式のタイプによっていくつかの異なるステージに分けて解く.Method->{s1->m1,s2->m2,…}では,ステージ si がメソッド miによって処理される.実際に使われるステージとその順序は,解こうとしている問題に基づいてNDSolveによって決定される.
- 使用可能な解法のステージ
-
"TimeIntegration" 微分方程式系の時間積分 "BoundaryValues" 常微分方程式の境界値解 "DiscontinuityProcessing" 不連続微分方程式を扱うための記号処理 "EquationSimplification" 数値評価のための方程式形式の簡略 "IndexReduction" 微分代数方程式の記号指数簡約 "DAEInitialization" 微分代数方程式の一貫した初期化 "PDEDiscretization" 偏微分方程式の離散化 - Method->m1 またはMethod->{m1,s2->m2,…}を使うと,メソッド m1は時間積分に使われると仮定されるので,Method->m1 はMethod->{"TimeIntegration"->m1}に等しい.
- Methodオプションの可能な明示的時間積分設定
-
"Adams" 一次から12次の予測器・修正子Adams法 "BDF" 一次から五次の陰的後退微分法 "ExplicitRungeKutta" 二次あるいは一次から九次あるいは八次のルンゲ・クッタ法の適応的埋込み型ペア "IDA" 微分代数方程式の陰的後退微分公式 "ImplicitRungeKutta" 任意次数の陰的ルンゲ・クッタ法の族 "SymplecticPartitionedRungeKutta" 分離可能なハミルトン系のためのインターリーブ・ルンゲ・クッタ法 - Method->{"controller",Method->"submethod"}あるいはMethod->{"controller",Method->{m1,m2,…}}のときの可能なコントローラ法
-
"Composition" サブメソッドのリストを作成 "DoubleStep" ダブルステップ法による刻み幅を適用 "EventLocator" 指定事象に応答 "Extrapolation" 多項式補外を用いて次数と刻み幅を適用 "FixedStep" 固定刻み幅を使用 "OrthogonalProjection" 直交制約条件を満たす解を投影 "Projection" 一般的な制約条件を満足する解を投影 "Splitting" 式を分割し異なるサブメソッドを使用 "StiffnessSwitching" 硬さが検出されたら陽的メソッドから陰的メソッドに変更 - 主にサブメソッドとして使われるメソッド
-
"ExplicitEuler" 前進オイラー法 "ExplicitMidpoint" 中点法則法 "ExplicitModifiedMidpoint" Graggの補整を伴う中点法則法 "LinearlyImplicitEuler" 線形陰的オイラー法 "LinearlyImplicitMidpoint" 線形陰的中点法則法 "LinearlyImplicitModifiedMidpoint" 線形陰的Bader補整中点法則法 "LocallyExact" 局所的に厳密な記号解の数値近似 - InterpolationOrder->Allと設定すると,NDSolveはもとになるメソッドと同じ次数の補間を使う解を生成するようになる. »
例題
すべて開く すべて閉じる例 (7)
スコープ (28)
オプション (31)
AccuracyGoalとPrecisionGoal (1)
InterpolationOrder (1)
MaxStepFraction (1)
積分区間の相対的に小さいサイズの特徴は見逃されることがある:
MaxStepFractionを使って区間の大きさにかかわらず特徴が見逃されないようにする:
MaxSteps (1)
MaxStepSize (2)
デフォルトのステップ制御では突然変化する特徴を見逃すことがある:
MaxStepSizeの設定値を小さくしてNDSolveが特徴を確実に捉えるようにする:
![]() より小さい正の整数の数を計算しようとするといくつかの事象を見逃してしまう:
より小さい正の整数の数を計算しようとするといくつかの事象を見逃してしまう:
MaxStepSizeを十分小さくして事象を一つも見逃さないようにする:
Method (14)
TimeIntegration (5)
PDEDiscretization (3)
BoundaryValues (1)
DiscontinuityProcessing (1)
EquationSimplification (2)
IndexReduction (1)
DAEInitialization (1)
初期化の前進コロケーションを使って0におけるAbsにまつわる問題を避ける:
アプリケーション (35)
常微分方程式 (5)
偏微分方程式 (10)
PDEModelsの概要には,さまざまな分野からの詳細な説明付きのPDEモデルの大規模コレクションが収められている.
表面を周期的に暖めた場合の深さ x における地熱の簡単なモデル:
Wolframの非線形波動方程式 [詳細]:
非線形シュレディンガー(Schrödinger)方程式における周期ポテンシャルによって摂動を与えられたソリトンの断面:

過度音圧場についてのモデル変数 vars をモデルパラメータ pars で定義する:
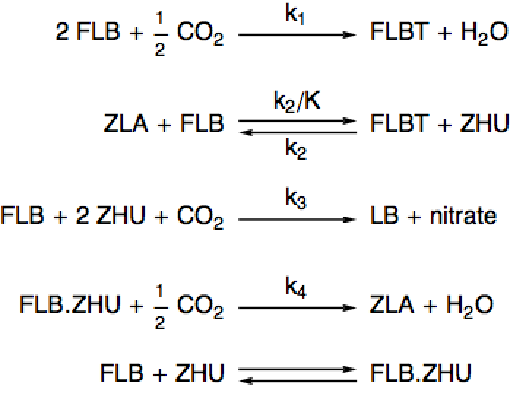
1つの反応速度でさまざまな材料を通過する1D化学種の移動をモデル化する.右辺と左辺はそれぞれ質量濃度と流入条件に従う:
ハイブリッド微分方程式 (5)
機械系 (3)
直交座標で振子の動きをモデル化する.ニュートンの運動の第2法則 ![]() および
および ![]() を示力図とともに使って支配方程式を導く:
を示力図とともに使って支配方程式を導く:
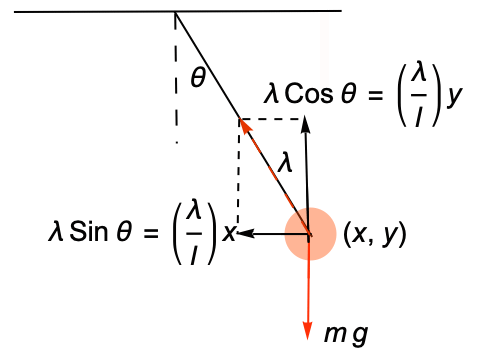
水平平面から放たれる,単位質量と単位長の二重振子をモデル化する.まず,ニュートンの運動の第2法則を使って方程式を導く:
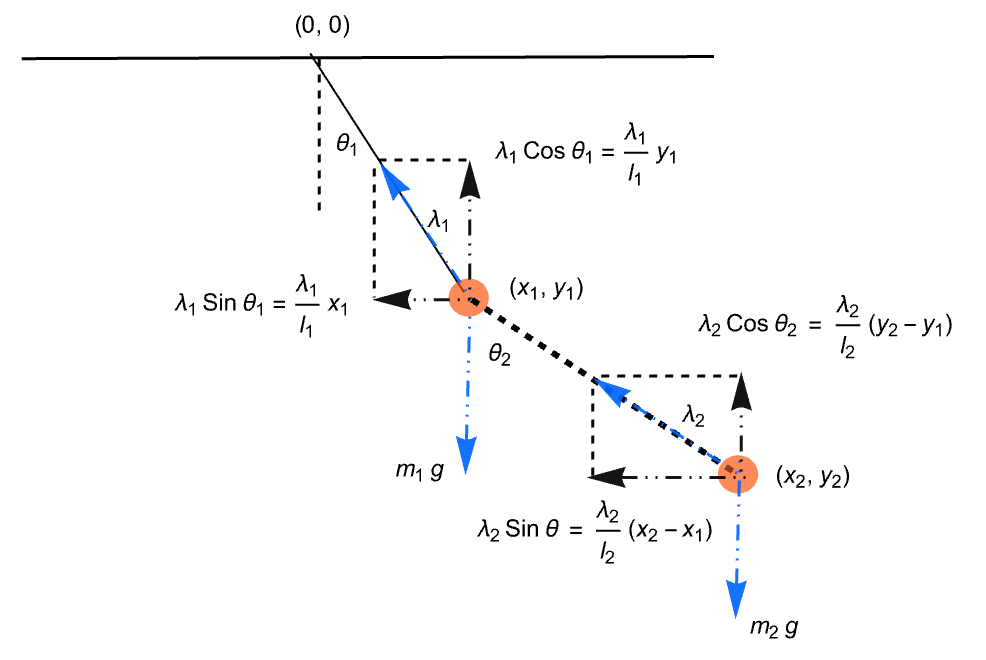
方程式と制約条件を不変量として強制することで,系のシミュレーションを行う:
動いているコンベヤベルト上の,粘度摩擦,クーロン摩擦,ストライベック摩擦,静摩擦を含むまざまな摩擦推力 ![]() を使ったバネで壁に固定されたブロックをモデル化する.各モデルについて位置と速度を比較する:
を使ったバネで壁に固定されたブロックをモデル化する.各モデルについて位置と速度を比較する:
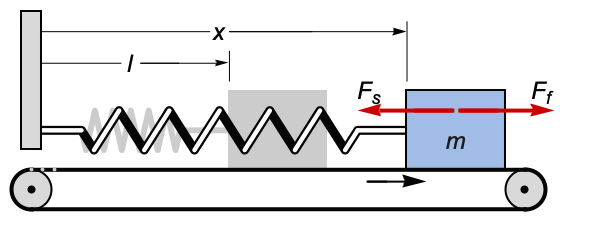
ストライベック摩擦は,バネの力がベルト表面の粗さに依存する値 μ を超えるまでブロックを一定の位置に保つ.離散変量 stuck は,ブロックが動かない場合は1に,それ以外の場合は0に設定する:
バネの力が μ より小さいかどうか,またブロックがベルトと相対的に移動していないかどうかをチェックする:
電気系 (6)
時間 ![]() ,電圧
,電圧 ![]() に対するRLC回路のステップ応答のシミュレーションを行う:
に対するRLC回路のステップ応答のシミュレーションを行う:
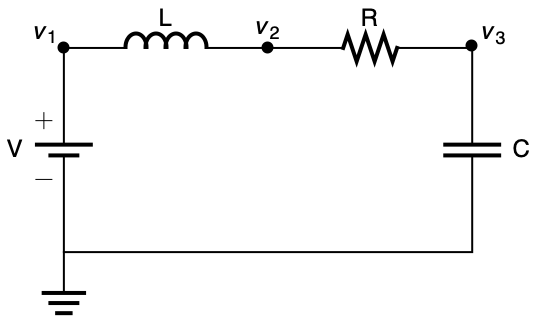
成分法則を接続に関するキルヒッホフ(Kirchhoff)の法則と一緒に使う:
時間 ![]() ,電圧
,電圧 ![]() に対するRLC回路のステップ応答のシミュレーションを行う:
に対するRLC回路のステップ応答のシミュレーションを行う:
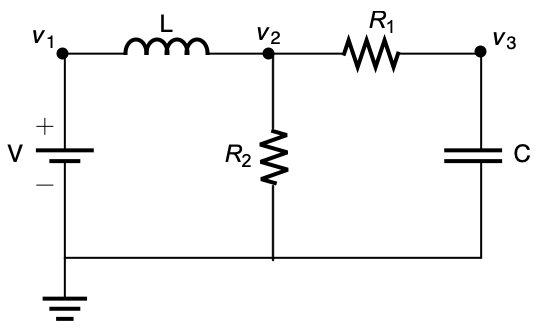
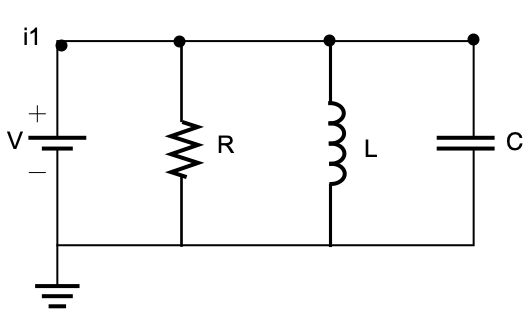
R,L,Cの各コンポーネントにおける電流とその結果の電圧を示す:
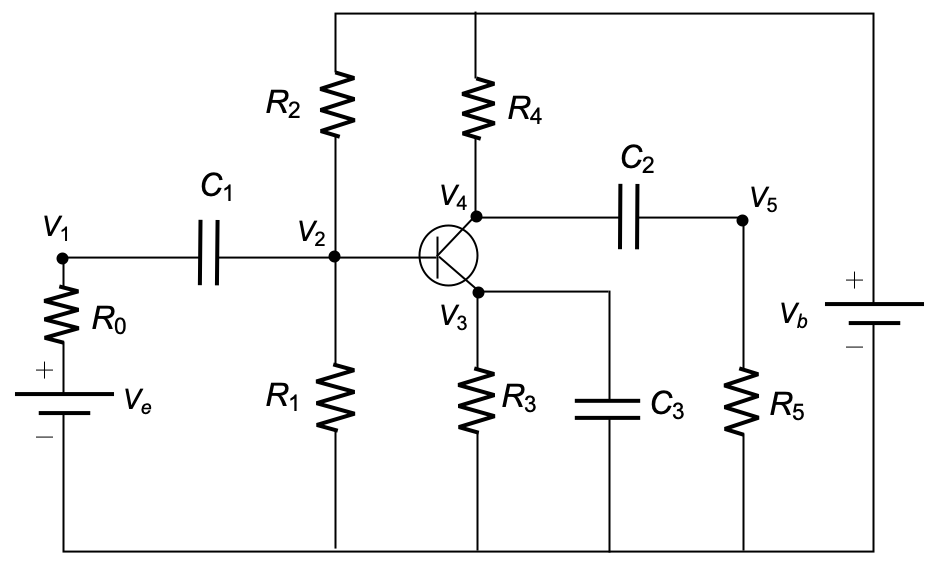
オームの法則とキルヒッホフの法則を使って各ノードの支配方程式を求める:
入力電圧レベル vi から希望する出力電圧レベル vd へのDC-DCブーストコンバータをパルス幅変調フィードバック制御 q[t]を使ってモデル化する:
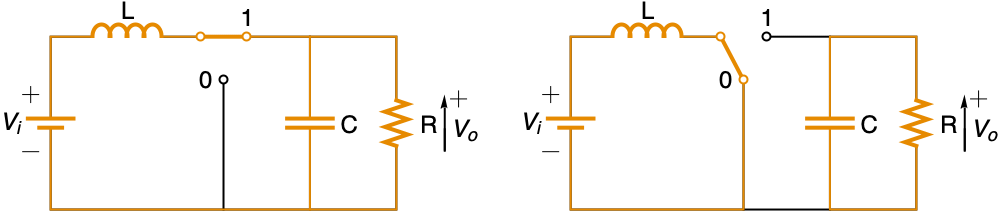
制御信号 q[t]が各周期 τ の vi/vd の割合でトランジスタをオンにする:
パルス幅変調フィードバック制御 q[t]を使って入力電圧レベル vi から希望する出力電圧レベルl vo へのDC-DC バックブーストコンバータをモデル化する:
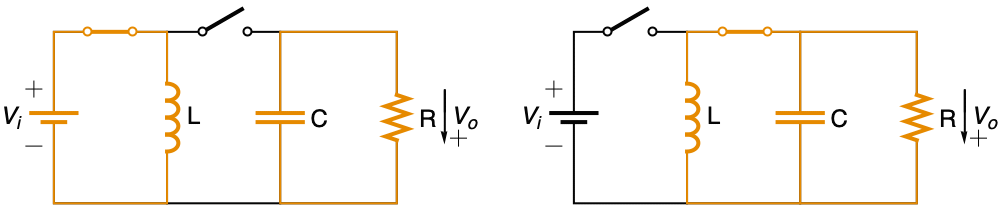
水力系 (3)
2本の円柱タンクがあり,水が一方のタンクからもう一方のタンクへとパイプを通って移動する.タンクの水面の高さの変化をモデル化する:
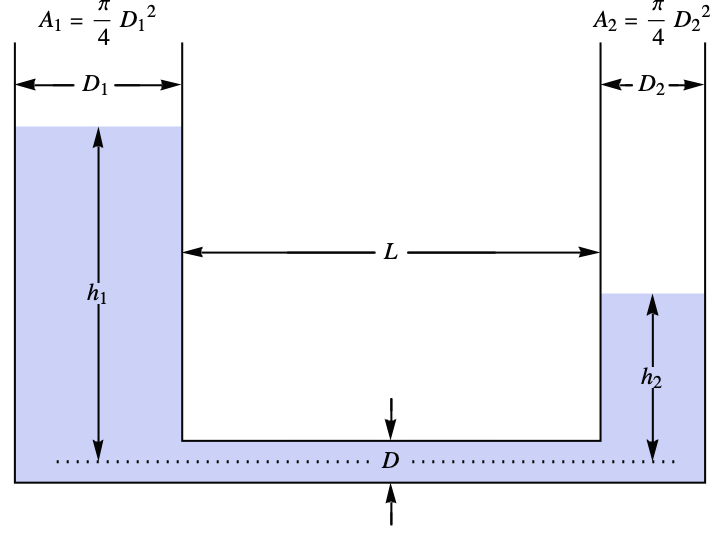
Hagen–Poiseuilleの関係を使ってパイプを通る流れのシミュレーションを行う:
2番目のタンクの水漏れのために,両方のタンクがいずれ空になる:
パイプを通って片方のタンクからもう一方のタンクに水が流れる.この半円形の2つのタンクの水位変化をモデル化する:
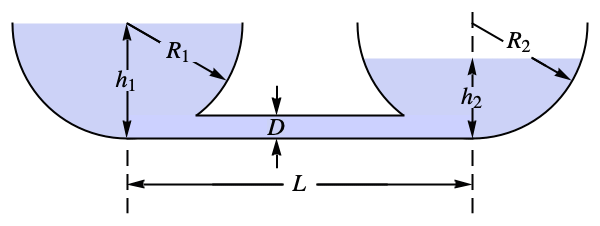
1つのタンクが他の2つのタンクに水を供給する3つのタンクがある.この3つのタンクの水位変化をモデル化する:
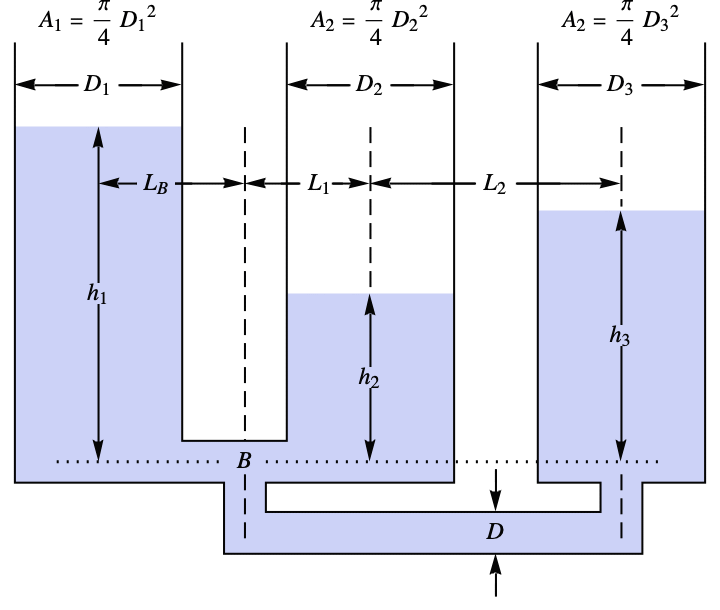
Hagen–Poiseuille関係でパイプを通る水の流れをモデル化する:
特性と関係 (7)
JacobiSNを定義する方程式:
独立変数の関数では,NDSolveは実質的に不定積分を返す:
NDSolveをSystemModelのソルバとして使う:
SystemModelを使って大きい階層的モデルをモデル化する:
考えられる問題 (14)
NDSolveのメッセージの多くにはそのメッセージに特有の参照ページがある.各ページにアクセスする方法はワークフローのエラーメッセージを理解するを参照されたい.
数値誤差 (4)
微分代数方程式 (3)
NDSolveは指数が1より大きい系を自動的には処理しない:
NDSolveは,![]() で解が求まらない場合は,指定された初期条件を変えることがある:
で解が求まらない場合は,指定された初期条件を変えることがある:
NDSolveは指数1に限定されるが,![]() の解の指数は2である:
の解の指数は2である:
高指数の系を解く場合は,指数減少法を使って微分代数方程式の指数を1にするとよい:
デフォルトのメソッドではデフォルトの許容度には収束できないかもしれない:
AccuracyGoalとPrecisionGoalの設定値を低くすると解が求まる:
偏微分方程式 (4)
PDEModelsの概要には,さまざまな分野からの詳細な説明付きのPDEモデルの大規模コレクションが収められている.
空間的な離散化は初期値に基づいており,それは最終値に比べると変化が少ない:

空間的な格子点の最小数を大きくすることで,最終値が正確に計算できるようになる:
このプロットは,空間的により複雑な解のオンセットを示している:
初期値における不連続性によって空間格子点が多すぎるようになるかもしれない:
空間格子点の数をより少なく設定しても,基本的に同じような解になる:
このソルバは初期値(Cauchy)問題としてよく設定できた方程式にしか使えない:

テクニカルノート
関連するガイド
-
▪
- 方程式の解法 ▪
- 微分方程式 ▪
- 偏微分方程式 ▪
- 領域におけるソルバ ▪
- 幾何学的計算 ▪
- メッシュベースの幾何学的領域 ▪
- 系のモデル化 ▪
- 記号的なベクトル,行列,配列 ▪
- 物理学と化学のデータと計算 ▪
- 数値的評価と精度 ▪
- 微積分 ▪
- 微分演算子 ▪
- 科学的モデル ▪
- 生命科学と医学のデータと計算 ▪
- 行列分解
履歴
1991 で導入 (2.0) | 1996 で更新 (3.0) ▪ 2003 (5.0) ▪ 2007 (6.0) ▪ 2008 (7.0) ▪ 2012 (9.0) ▪ 2014 (10.0) ▪ 2019 (12.0)
テキスト
Wolfram Research (1991), NDSolve, Wolfram言語関数, https://reference.wolfram.com/language/ref/NDSolve.html (2019年に更新).
CMS
Wolfram Language. 1991. "NDSolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/NDSolve.html.
APA
Wolfram Language. (1991). NDSolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NDSolve.html
BibTeX
@misc{reference.wolfram_2025_ndsolve, author="Wolfram Research", title="{NDSolve}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/NDSolve.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_ndsolve, organization={Wolfram Research}, title={NDSolve}, year={2019}, url={https://reference.wolfram.com/language/ref/NDSolve.html}, note=[Accessed: 07-February-2026]}