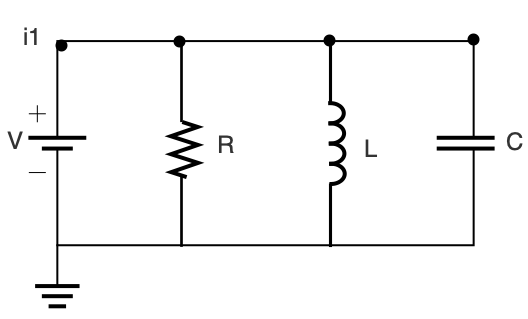NDSolve
NDSolve[eqns,u,{x,xmin,xmax}]
求解函数 u 的常微分方程 eqns 的数值解,自变量 x 位于从 xmin 到 xmax 的范围内.
NDSolve[eqns,u,{x,xmin,xmax},{y,ymin,ymax}]
在矩形区域上求解偏微分方程 eqns.
NDSolve[eqns,u,{x,y}∈Ω]
在区域 Ω 上求解偏微分方程 eqns.
NDSolve[eqns,u,{t,tmin,tmax},{x,y}∈Ω]
在区域 Ω 上求解时间相关偏微分方程 eqns.
NDSolve[eqns,{u1,u2,…},…]
求解函数 ui.
更多信息和选项




- NDSolve 是一个数字微分方程求解器,用 InterpolatingFunction 对象给出结果.
- NDSolve[eqns,u[x],{x,xmin,xmax}] 给出 u[x] 而不是函数 u 本身的解.
- 微分方程必须使用诸如 u'[x] 的导数表示,用 D 求解,而不是用 Dt 求得的总导数.
- 偏微分方程也可能使用微分算子 Grad (∇)、Div (∇.)、Laplacian (∇2) 和 Curl (∇) 指定. 通常这些算子用于 Inactive[op] 中以使得算子形式不用计算.
- NDSolve 可以求解广泛的常微分方程,以及许多偏微分方程.
- NDSolve 还可以用来求解时滞微分方程.
- 在常微分方程中函数 ui 只能依赖与单个变量 t. 在偏微分方程中它们可以依赖于多个变量.
- WhenEvent[event,action] 可能包含在方程 eqns 中,以指定当 event 变成 True 时,出现的 action.
- 微分方程必须包括足够的初始条件或边界条件来完全确定 ui 的解.
- 初始和边界条件通常用格式 u[x0]==c0、u'[x0]==dc0 等表示,但是可能包含更复杂的方程.
- c0、 dc0 等可以是列表,指定 u[x] 是一个具有向量值或者普通列表值的函数.
- 周期性边界条件可以使用 u[x0]==u[x1] 指定.
- 出现在初始或者边界条件中的点 x0 不需要位于搜索解的从 xmin 到 xmax 的范围内.
- 边界值也可以使用 DirichletCondition 和 NeumannValue 指定.
- 在时滞微分方程中,初始历史函数以格式 u[x/;x<x0]==c0 给出,其中 c0 通常是关于 x 的函数.
- NDSolve 中的微分方程可以包含复数.
- NDSolve 可以求解许多微分代数方程,即某些 eqns 是纯代数的,或某些变量可以是隐式代数的.
- ui 可以使有应变量的函数,不需要包含所有这样的变量.
- 可以给出以下选项:
-
AccuracyGoal Automatic 所寻求的绝对精度的位数 Compiled Automatic 表达式是否应该自动编译 DependentVariables Automatic 所有应变量的列表 EvaluationMonitor None 每当计算函数时需要计算的表达式 InitialSeeding {} 用于某些算法的播种方程 InterpolationOrder Automatic 最终输出的连续性度数 MaxStepFraction 1/10 每个步骤所覆盖求解范围的最大比例 MaxSteps Automatic 采用步骤的最大数目 MaxStepSize Automatic 每个步骤的最大步长 Method Automatic 使用的方法 NormFunction Automatic 误差估计使用的范数 PrecisionGoal Automatic 所寻求的精度的位数 StartingStepSize Automatic 初始步长 StepMonitor None 每进行一个步骤时,要计算的表达式 WorkingPrecision MachinePrecision 内部计算使用的精度 - NDSolve 会调整步长,使解中的估计误差在 PrecisionGoal 和 AccuracyGoal 指定的容差内.
- 选项 NormFunction->f 指定每个 ui 的估计误差需要用 f[{e1,e2,…}] 进行组合.
- AccuracyGoal 实际上指定了求解时每一步所允许的绝对局部误差,而 PrecisionGoal 指定相对局部误差.
- 如果解的值接近 0,而且要准确地逼近该解, 则 AccuracyGoal 的设置应该较大,或是 Infinity.
- AccuracyGoal 和 PrecisionGoal 的缺省设置 Automatic 等于 WorkingPrecision/2.
- MaxSteps 的默认设置 Automatic 估计 NDSolve 所采用的最大步骤数目,取决于开始和结束时间,以及步长的估计值. 如果无法得到这些,就采用固定的步骤数目.
- MaxStepFraction 的设置指定 NDSolve 采用的最大步长应该是每个独立变量值范围的几分之几.
- 在 DependentVariables->Automatic 设置下,NDSolve 通过分析给定的方程尽可能的确定应变量.
- 取决于方程的类型,NDSolve 通常通过几个不同的阶段求解微分方程. 设置 Method->{s1->m1,s2->m2,…},阶段 si 由方法 mi 处理. 使用的实际阶段和它们的阶数基于所要解决的问题,由 NDSolve 决定.
- 可能的求解步骤是:
-
"TimeIntegration" 微分方程组的时间积分 "BoundaryValues" 常微分方程边界值的解 "DiscontinuityProcessing" 用于处理不连续微分方程的符号式处理 "EquationSimplification" 用于数值计算的方程的化简 "IndexReduction" 用于微分代数方程的符号式指标化简 "DAEInitialization" 用于微分代数方程的一致初始化 "PDEDiscretization" 用于偏微分方程离散化 - 设置 Method->m1 或者 Method->{m1,s2->m2,…},假定方法 m1 用于时间积分,因此 Method->m1 等价于 Method->{"TimeIntegration"->m1}.
- Method 选项的可能显式时间积分设置包括:
-
"Adams" 阶数从 1 到 12 的预估-校正 Adams 方法 "BDF" 阶数从 1 到 5 的隐式向后微分公式 "ExplicitRungeKutta" 从 2(1) 到 9(8) 的 Runge‐Kutta 方法的自适应嵌入对 "IDA" DAE 的隐式反向微分公式 "ImplicitRungeKutta" 任意次数的隐式 Runge‐Kutta 方法系列 "SymplecticPartitionedRungeKutta" 对可分 Hamiltonian 系统交叉存取的 Runge‐Kutta 方法 - 在设置 Method->{"controller",Method->"submethod"} 或Method->{"controller",Method->{m1,m2,…}} 下,可能的控制方法包括:
-
"Composition" 组建一个子方法列表 "DoubleStep" 用双倍步长方法来自适应步长 "EventLocator" 对指定事件的响应 "Extrapolation" 用多项式插值方法来自适应阶数与步长 "FixedStep" 用一个固定的步长 "OrthogonalProjection" 投影解来满足正交约束条件 "Projection" 投影解来满足普通约束条件 "Splitting" 分割方程并用不同的子方法 "StiffnessSwitching" 检测到刚性时,从显式到隐式的切换 - 主要用作子方法的方法包括:
-
"ExplicitEuler" 向前欧拉方法 "ExplicitMidpoint" 中点法则 "ExplicitModifiedMidpoint" 有 Gragg 平滑化的中点法则 "LinearlyImplicitEuler" 线性隐式 Euler 方法 "LinearlyImplicitMidpoint" 线性隐式中点法则 "LinearlyImplicitModifiedMidpoint" 线性隐式 Bader‐平滑化的中点法则 "LocallyExact" 对局部精确符号解的数值近似 - 设置 InterpolationOrder->All 指定 NDSolve 所产生解的插值阶数要与所用方法的阶数相同. »
范例
打开所有单元关闭所有单元基本范例 (7)
范围 (28)
常微分方程 (8)
偏微分方程 (5)
边界值问题 (5)
选项 (31)
InterpolationOrder (1)
MaxStepFraction (1)
用 MaxStepFraction 确保这些特征不会丢失,使其不依赖于积分区间的大小:
MaxStepSize (2)
一个较小的 MaxStepSize 设置确保 NDSolve 捕捉到这个特征:
设置足够小的 MaxStepSize 来确保没有事件遗漏:
Method (14)
TimeIntegration (5)
PDEDiscretization (3)
DiscontinuityProcessing (1)
EquationSimplification (2)
IndexReduction (1)
DAEInitialization (1)
对初始化,使用向前搭配(collocation),以避免0处 Abs 项的问题:
应用 (35)
常微分方程 (5)
偏微分方程 (10)
在 PDE models overview 中可以找到各个领域的大量 PDE 模型以及详细的说明.
Wolfram 非线性波动方程 [更多信息]:
在非线性薛定谔方程中由一个周期性的潜在势阱扰动的孤子的配置文件:
混合微分方程 (5)
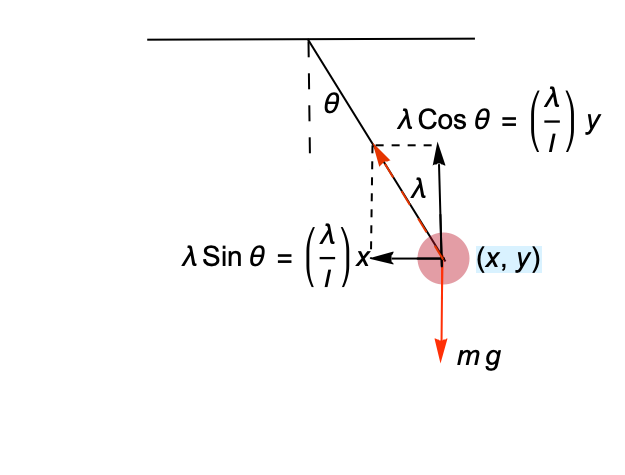
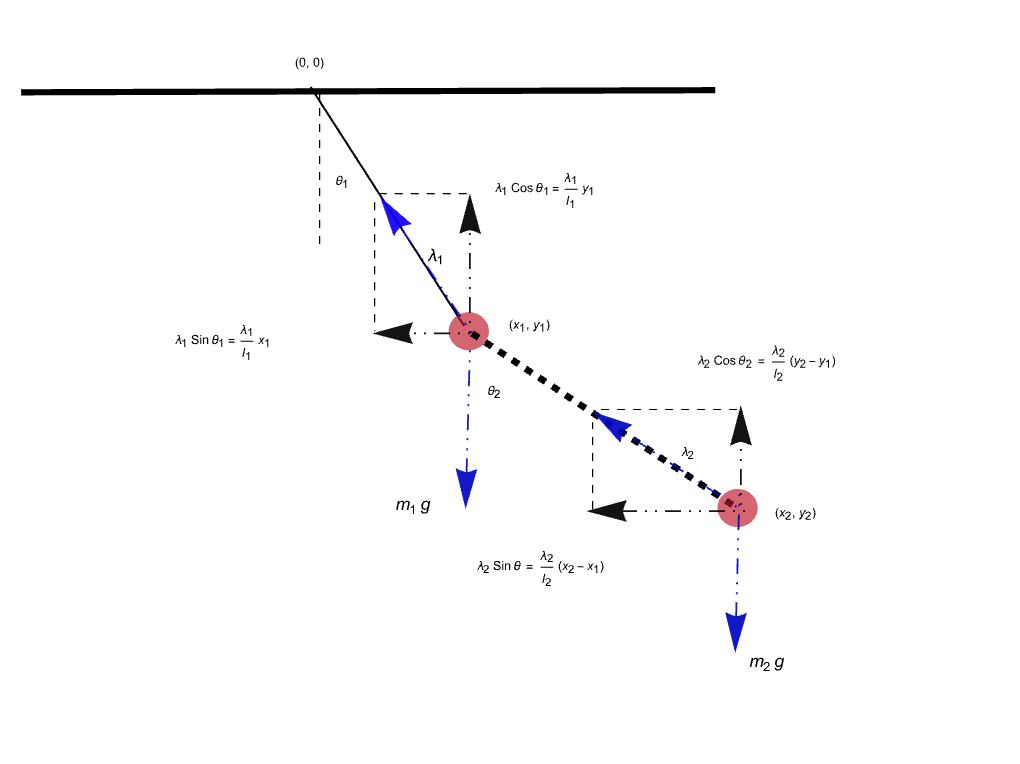
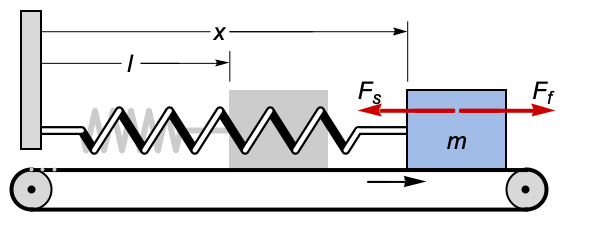
机械系统 (3)
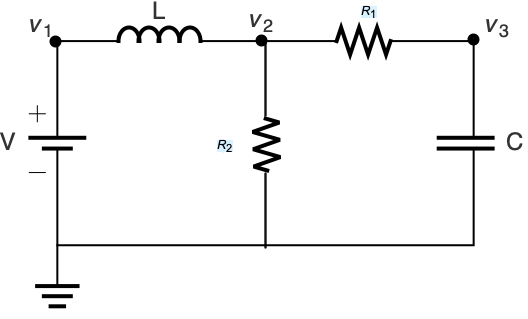
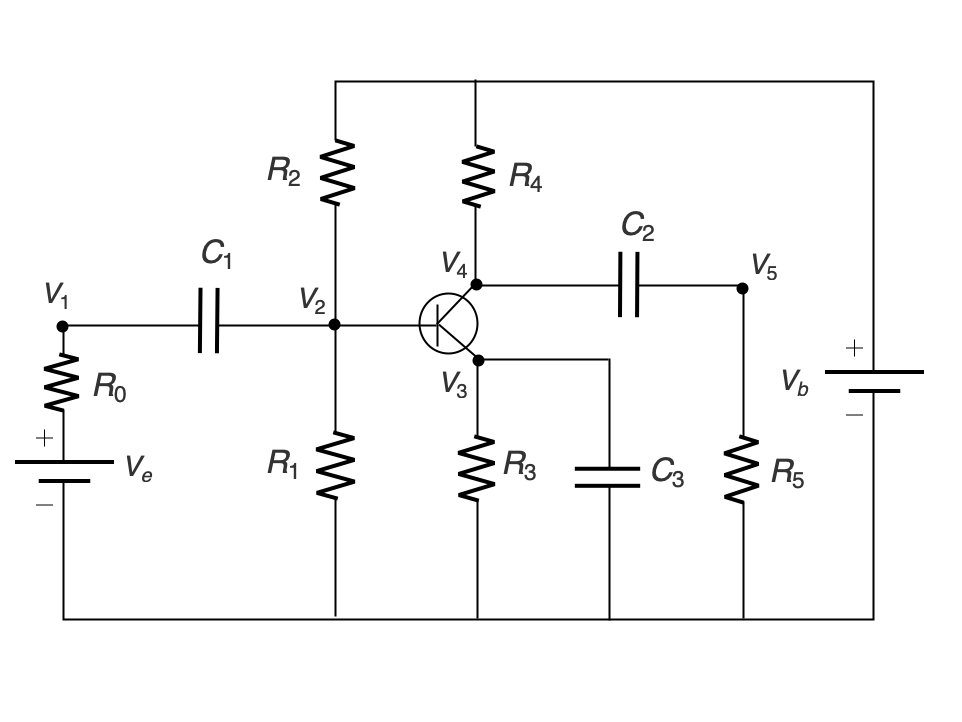
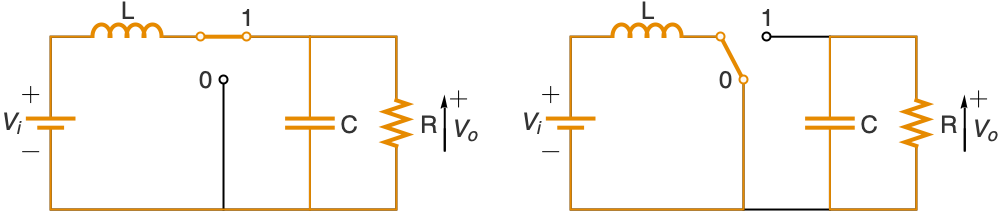
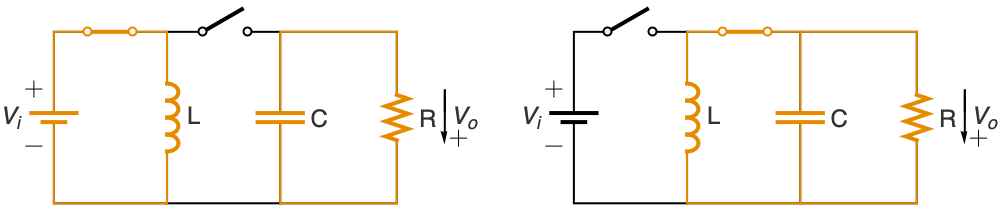
电子系统 (6)
属性和关系 (7)
JacobiSN 的定义方程:
对于自变量的函数,NDSolve 实际上给出不定积分:
事件定位(Event location) 可准确而有效地找到根:
使用 NDSolve 作为 SystemModel 的求解器:
使用 SystemModel 模拟更大型的分层模型:
可能存在的问题 (14)
针对许多 NDSolve 消息,有特定的消息参考页面. 请到理解出错消息工作流程中了解怎样访问这些页面.
数值误差 (4)
微分代数方程 (3)
NDSolve 不能自动处理指标大于1的方程组:
如果在 ![]() 的条件下无法找到解,NDSolve 可以改变指定的初始条件:
的条件下无法找到解,NDSolve 可以改变指定的初始条件:
NDSolve 仅限于指标1方程,但 ![]() 时解的指标为2:
时解的指标为2:
在较低的 AccuracyGoal 和 PrecisionGoal 设置下,可求得一个解:
偏微分方程 (4)
文本
Wolfram Research (1991),NDSolve,Wolfram 语言函数,https://reference.wolfram.com/language/ref/NDSolve.html (更新于 2019 年).
CMS
Wolfram 语言. 1991. "NDSolve." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/NDSolve.html.
APA
Wolfram 语言. (1991). NDSolve. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/NDSolve.html 年