PERTDistribution
PERTDistribution[{min,max},c]
範囲が min から max までで c で最頻値になるPERT分布を表す.
PERTDistribution[{min,max},c,λ]
形状母数が λ の修正PERT分布を表す.
詳細

- PERTDistributionはパート法(program evaluation and review technique,略してPERT)でプロジェクト完遂までの時間分析に使われるもので,事実上BetaDistributionを再パラメータ化したものである.
- PERTDistributionはベータ-PERT分布としても知られている.
- PERTDistribution[{min,max},c,λ]はTransformedDistribution[min+x(max-min),xBetaDistribution[1+λ
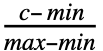 ,1+λ
,1+λ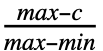 ]]に等しい.
]]に等しい. - PERTDistributionでは,min,max,c は min<c<max となるような任意の実数でよく,λ は任意の非負の実数でよい.
- PERTDistributionでは,min,max,c は単位次元が等しい任意の数量でよく,λ は無次元量でよい. »
- PERTDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- PERTDistributionは,一様分布あるいは三角分布(Wolfram言語ではそれぞれUniformDistributionおよびTriangularDistributionとして実装されている)の,平滑で潜在的に歪んでいるバージョンを表す.これは,単一の峰を持ち,有限区間で定義される.より正確に言うなら,PERTDistribution[{min,max},c,λ]は,c および λ≥0の2つの定数によってパラメータ化された min から max までの値について定義される統計分布を表す.ここで,c は分布の最頻値で,確率密度関数(PDF)の峰の位置を決定する.これに対し,λ は c ともにPDFの全体的な形を決定する「形状母数」である.2引数形のPERTDistribution[{min,max},c]はPERTDistribution[{min,max},c,4]に等しい.
- 「PERT」は「project evaluation and review techniques(プロジェクト評価と検討の技術)」の頭字語であり,最小値および最大値についての専門家の推定を与えられた場合の,所望の数量(プロジェクトの完了時期等)およびその数量で最も可能性の高い値についての専門家の推定をモデル化する分布の大規模使用を意味する.PERT分布はベータPERT分布と呼ばれることもある.
- RandomVariateを使って,PERT分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,PERTDistribution[{min,max},c,λ]](より簡略すると xPERTDistribution[{min,max},c,λ])を使って,確率変数 x がPERT分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[PERTDistribution[{min,max},c,λ],x]およびCDF[PERTDistribution[{min,max},c,λ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がPERT分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックPERT分布を推定することが,FindDistributionParametersを使ってデータをPERT分布にフィットすることができる.ProbabilityPlotを使って記号PERT分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号PERT分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたPERT分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってPERT分布を含む高次元分布を構築することが,ProductDistributionを使ってPERT分布を含む独立成分分布の結合分布を計算することができる.
- PERTDistributionは他の多くの分布と密接に関係している.例えば,PERT分布は変換されたBetaDistribution(より正確には PERTDistribution[{min,max},c,λ]はTransformedDistribution[min+x(max-min),xBetaDistribution[1+λ
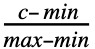 ,1+λ
,1+λ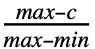 ]]と等しい)と定義することができ,TriangularDistributionの平滑化されたバージョンとして使うことができる.PERTDistributionは,BetaDistributionとの密接な関係のため,UniformDistributionおよびPowerDistributionのあまり直接的ではない一般化と考えることができる.BetaDistributionと同様に,PERTDistributionはKumaraswamyDistributionおよびNoncentralBetaDistributionの変換によって得ることができる.また,BetaDistributionのように,PERTDistributionはPearsonDistribution,ChiSquareDistribution,GammaDistribution,FRatioDistribution,BetaPrimeDistributionと密接な関係がある.
]]と等しい)と定義することができ,TriangularDistributionの平滑化されたバージョンとして使うことができる.PERTDistributionは,BetaDistributionとの密接な関係のため,UniformDistributionおよびPowerDistributionのあまり直接的ではない一般化と考えることができる.BetaDistributionと同様に,PERTDistributionはKumaraswamyDistributionおよびNoncentralBetaDistributionの変換によって得ることができる.また,BetaDistributionのように,PERTDistributionはPearsonDistribution,ChiSquareDistribution,GammaDistribution,FRatioDistribution,BetaPrimeDistributionと密接な関係がある.
例題
すべて開くすべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
λ の値が大きいと,尖度はNormalDistributionの尖度に近付く:
母数でQuantityを一貫して使用するとQuantityDistributionが返される:
アプリケーション (2)
ある専門家の推定では,完成までに4〜6ヶ月かかるプロジェクトが5ヶ月と1週間かかるという:
PERTDistributionを TriangularDistributionの平滑化された代替物として使う:
特性と関係 (5)
PERT分布は平行移動と正の因子によるスケーリングの下では閉じている:
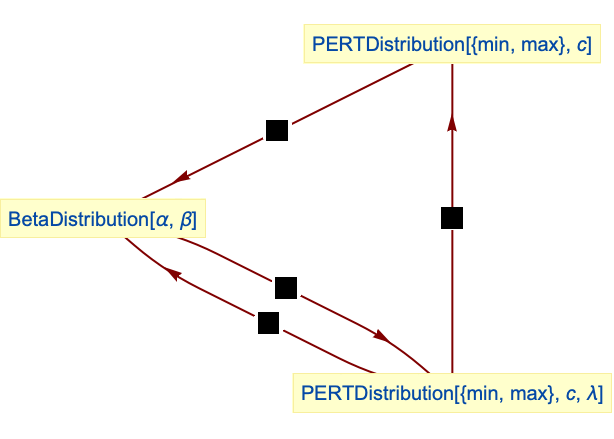
PERT分布はBetaDistributionを変換したものである:
母数が ![]() および
および ![]() のBetaDistributionは,単位区間におけるPERTDistributionの特殊ケースである:
のBetaDistributionは,単位区間におけるPERTDistributionの特殊ケースである:
テキスト
Wolfram Research (2010), PERTDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/PERTDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "PERTDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/PERTDistribution.html.
APA
Wolfram Language. (2010). PERTDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PERTDistribution.html