WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

PairCorrelationG[pdata,r]

半径 r の点データ pdata について対相関関数 を推定する．

PairCorrelationG[pproc,r]

点過程 pproc について を計算する．

PairCorrelationG[bdata,r]

ビン分割されたデータ bdata について を計算する．

PairCorrelationG[pspec]

異なる半径 r に繰り返し適用できる関数 を生成する．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
点データ  
点過程  
オプション  
Method  
SpatialBoundaryCorrection  
アプリケーション  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

PairCorrelationG

PairCorrelationG[pdata,r]

半径 r の点データ pdata について対相関関数 を推定する．

PairCorrelationG[pproc,r]

点過程 pproc について を計算する．

PairCorrelationG[bdata,r]

ビン分割されたデータ bdata について を計算する．

PairCorrelationG[pspec]

異なる半径 r に繰り返し適用できる関数 を生成する．

詳細とオプション

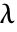  • が平均密度である積 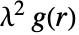は距離が 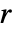離れている2つの点を見付ける確率密度である．
  •     
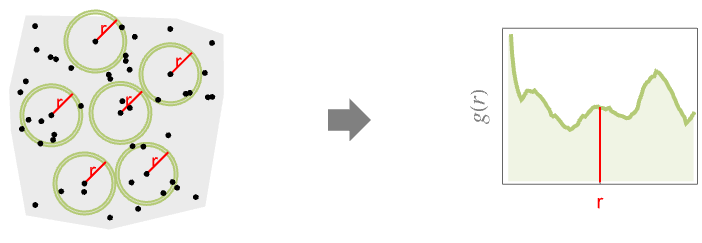
  • PairCorrelationGは，値が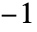から1まで変化する通常の意味の相関ではない．範囲は0から 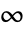までで，1が完全な空間的ランダム性に相当する．
  • PairCorrelationGは距離 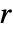における点の相関の空間的均一性を測定する．ポアソン点過程と比べると以下のようになる．
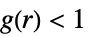
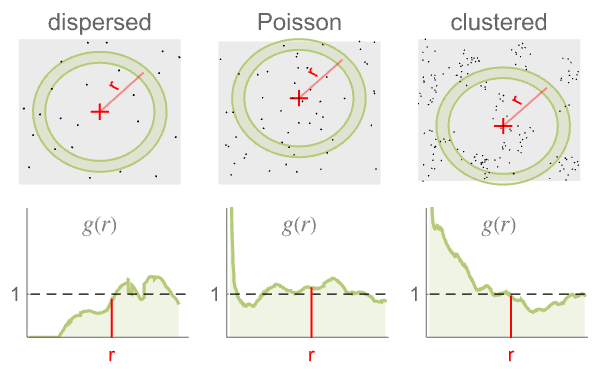
  • ポアソン点過程よりも分散している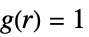
    ポアソン点過程のようである．つまり，完全な空間的ランダム性を呈している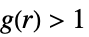
    ポアソン点過程よりもクラスタ化している
  •     
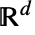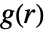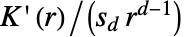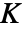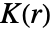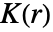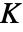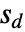  • の等方性定常点過程については，対相関関数 は，単位球の測度 で正規化されたRipleyの 関数 の導関数である．ただし， はRipleyの 関数で は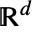における単位球の測度である．
  • 半径 r は単一の値でも値のリストでもよい．半径 r が指定されていないとPairCorrelationGはPointStatisticFunctionを返す．これを使って 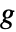関数を繰り返し評価することができる．
  • 点 pdata の形は以下でよい．
  • {p1,p2,…}点 pi
    GeoPosition[…],GeoPositionXYZ[…],…地理的な点
    SpatialPointData[…]空間的な点集合
    {pts,reg}点集合 pts と観測領域 reg
  • 観測領域 reg は，与えられていない場合はRipleyRassonRegionを使って自動的に計算される．
  • 点過程 pproc は以下の形でよい．
  • proc点過程 proc
    {proc,reg}点過程 proc と観測領域 reg
  • 観測領域 reg はパラメータフリーで，SpatialObservationRegionQでなければならない．
  • ビン分割されたデータ bdata はSpatialBinnedPointDataからのもので，区分一定密度関数によってInhomogeneousPoissonPointProcessとして扱われる．
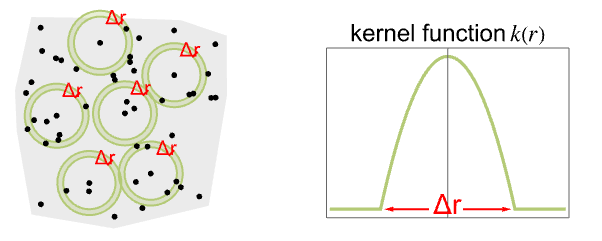
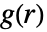  • は，pdata についてはカーネル平滑化 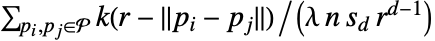を使って計算される．ただし，追加的な辺補正が適用される．ここで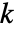， は平滑化カーネルで 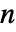は点の数である．
  •     
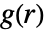  • は，pproc については厳密な式を使って計算されるかシミュレーションを使って点データを生成するかする．
  • 次は，使用可能なオプションである．
  • Method Automatic使用するメソッド
    SpatialBoundaryCorrection Automatic使用する境界補正
  • SpatialBoundaryCorrectionには次の設定を使うことができる．
  • Automatic境界補正を自動的に決定する
    "BorderMargin"観測領域に内部余白を使う
    None境界補正なし
    "Ripley"点から境界までの距離による重みを使う
  • Method{"Kernel"->kern,"Bandwidth"->bw}の設定では，推定の平滑化カーネル kern と帯域幅 bw を選ぶことができる．ここで，kern は組込みのKernelMixtureDistributionがサポートしている一次元カーネルでよく，帯域幅 bw はAutomaticもしくは任意の正の数でよい．
  • デフォルトで，"Epanechnikov"カーネルが使われ，帯域幅は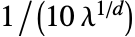になるように選ばれる．
  • PairCorrelationGは，RipleyKまたはBesagLによって生成されたPointStatisticFunctionからの対相関関数を推定することができる．スプラインを平滑化することで推定する．このシミュレーションでは，引数 pdata が以下の形と解釈を持つ．
  • {PointStatisticFunction[…],{r1,r2,dr}}距離Range[r1,r2,dr]で取られたサンプルの値に基づいて対相関関数を推定する
    {PointStatisticFunction[…],{{r1,r2,…}}}距離{r1,r2,...}で取られたサンプルの値に基づいて対相関関数を推定する
    {PointStatisticFunction[…],rspec,type}type で指定される平滑化で上記と同じことをする
  • 次は，サポートされる平滑化タイプである．
  • 1平滑化スプラインを 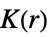に適用する（デフォルト）
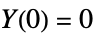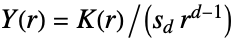    2平滑化スプラインを制約条件 で に適用する
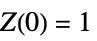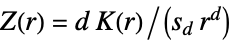    3平滑化スプラインを制約条件でに適用する
    4平滑化スプラインを 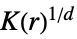に適用する

例題

すべて開く すべて閉じる

例  (3)

指定された半径における対相関関数を推定する：

Wolfram Language code: region = Ball[{0, 0}]; pts = RandomPoint[region, 100];
Wolfram Language code: PairCorrelationG[{pts, region}, 0.2]

距離の範囲内で対相関関数を推定する：

Wolfram Language code: spd = SpatialPointData[RandomReal[1, {500, 2}]]
Wolfram Language code: rspec = Range[0.1, 0.4, 0.01];
Wolfram Language code: est = PairCorrelationG[spd, rspec];

ListPlotで結果を可視化する：

Wolfram Language code: ListPlot[est, DataRange -> MinMax[rspec], Filling -> Axis, AxesLabel -> {r}]

クラスタ点過程の対相関関数：

Wolfram Language code: pcf = PairCorrelationG[ThomasPointProcess[μ, λ, σ, 2], r]

指定されたパラメータ値で関数を可視化する：

Wolfram Language code: Plot[pcf /. {μ -> 3, λ -> 2, σ -> 1}, {r, 0, 3}, AxesLabel -> {r}]

スコープ  (9)

点データ  (6)

距離0.03における対相関関数を推定する：

Wolfram Language code: region = Rectangle[{0, 0}, {1, 2}]; pts = RandomPoint[region, 100];
Wolfram Language code: PairCorrelationG[{pts, region}, 0.03]

指定された距離のリストから対相関関数の経験的推定を得る：

Wolfram Language code: PairCorrelationG[{pts, region}, {0.01, 0.02, 0.05, 0.1}]

PairCorrelationをSpatialPointDataと一緒に使う：

Wolfram Language code: spd = SpatialPointData[RandomReal[1, {500, 3}]]
Wolfram Language code: res = PairCorrelationG[spd, {0.01, 0.02}]

将来的に使うためにPointStatisticFunctionを作る：

Wolfram Language code: reg = Disk[]; pts = RandomPoint[Disk[], 100];
Wolfram Language code: psf = PairCorrelationG[{pts, reg}]

与えられた半径で値を計算する：

Wolfram Language code: psf[0.1]

観測領域を明示的に与えることなしに対相関関数を推定する：

Wolfram Language code: BlockRandom[SeedRandom[1]; pts = RandomReal[1, {100, 2}] ];
Wolfram Language code: psf = PairCorrelationG[pts]

Ripley–Rasson推定器によって生成された観測領域：

Wolfram Language code: psf["ObservationRegion"]

対相関関数を距離0.05において推定する：

Wolfram Language code: psf[0.05]

PairCorrelationをGeoPositionと一緒に使う：

Wolfram Language code: pts = RandomGeoPosition[GeoDisk[GeoPosition[{0, 0}], Quantity[10, "Kilometers"]], 10 ^ 2]
Wolfram Language code: psf = PairCorrelationG[pts]

点統計関数をプロットする：

Wolfram Language code: ListPlot[Table[{x, psf[x]}, {x, Quantity[0, "km"], psf["MaxRadius"], Quantity[.1, "km"]}], AxesLabel -> {"km"}]

関数からの対相関関数をさまざまな平滑化メソッドで推定する：

Wolfram Language code: reg = Ball[]; pts = RandomPoint[reg, 10 ^ 3];

Ripleyの 関数を計算する：

Wolfram Language code: rk = RipleyK[{pts, reg}]

対相関を指定された半径であらゆる平滑化メソッドを使って推定する：

Wolfram Language code: rlist = Range[0.01, 0.3, 0.01]; pcfs = PairCorrelationG[{rk, {0, 0.3, 0.01}, #}, rlist]& /@ Range[4];

推定値をさまざまな平滑化メソッドで可視化する：

Wolfram Language code: ListLinePlot[pcfs, DataRange -> MinMax[rlist], AxesLabel -> {r}, PlotLegends -> (Row[{"smoothing method ", #}]& /@ Range[4])]

点過程  (3)

PoissonPointProcessについての対相関は一定である：

Wolfram Language code: proc = PoissonPointProcess[μ, d];
Wolfram Language code: PairCorrelationG[proc, r]

クラスタ過程ThomasPointProcessについての対相関：

Wolfram Language code: proc = ThomasPointProcess[μ, λ, rad, d];
Wolfram Language code: PairCorrelationG[proc, r]

固定された過程パラメータと変化する次元について可視化する：

Wolfram Language code: nproc = proc /. {μ -> 20, λ -> 10, rad -> .2};
Wolfram Language code: Plot[Table[PairCorrelationG[nproc, r], {d, 1, 4}]//Evaluate, {r, 0, 1}, AxesLabel -> {r}, PlotLegends -> (Row[{#, "D"}]& /@ Range[4])]

クラスタ過程MaternPointProcessについての対相関：

Wolfram Language code: proc = MaternPointProcess[μ, λ, σ, d];
Wolfram Language code: PairCorrelationG[proc, r]

固定された過程パラメータと変化する次元について可視化する：

Wolfram Language code: nproc = proc /. {μ -> 20, λ -> 10, σ -> .4};
Wolfram Language code: Plot[Table[PairCorrelationG[nproc, r], {d, 1, 4}]//Evaluate, {r, 0, 1}, AxesLabel -> {r}, PlotLegends -> (Row[{#, "D"}]& /@ Range[4])]

オプション  (2)

Method  (1)

カーネル平滑化設定はMethodのサブオプションとして与えることができる：

Wolfram Language code: region = Triangle[{{0, 0}, {1, 2}, {-3, 1}}]; pts = RandomPoint[region, 100];

同じ半径の異なるカーネル関数で対相関関数を推定する：

Wolfram Language code: PairCorrelationG[{pts, region}, 0.05, Method -> {"Kernel" -> #}]& /@ {"Epanechnikov", "Cosine", "Biweight"}

異なる帯域幅を使って同じ半径の対相関関数を推定する：

Wolfram Language code: PairCorrelationG[{pts, region}, 0.05, Method -> {"Bandwidth" -> #}]& /@ {0.01, 0.02, 0.03}

SpatialBoundaryCorrection  (1)

境界補正がないPairCorrelationG推定器は偏っており，大きい点集合以外では使われるべきではない：

Wolfram Language code: region = Rectangle[{0, 0}, {1, 2}]; pts = RandomPoint[region, 100];
Wolfram Language code: PairCorrelationG[{pts, region}, 0.05, SpatialBoundaryCorrection -> "None"]

デフォルトメソッドの"BorderMargin"は境界から距離 の点だけを考慮する：

Wolfram Language code: PairCorrelationG[{pts, region}, 0.05, SpatialBoundaryCorrection -> "BorderMargin"]

境界補正メソッドの"Ripley"は点の各ペアに重みを付けて推定器の偏りを正す：

Wolfram Language code: PairCorrelationG[{pts, region}, 0.05, SpatialBoundaryCorrection -> "Ripley"]

アプリケーション  (2)

完全な空間ランダム性における対相関関数：

Wolfram Language code: region = Ellipsoid[{0, 0}, {2, 3}]; pts = RandomPoint[region, 500];

与えられたデータで対相関関数の値を推定する：

Wolfram Language code: rspec = Range[0.02, 0.8, 0.02]; data = PairCorrelationG[{pts, region}, rspec];

結果を可視化する：

Wolfram Language code: ListPlot[{data, Transpose[{MinMax[rspec], {1, 1}}]}, DataRange -> MinMax[rspec], Joined -> {False, True}, PlotLegends -> {"estimated", "theoretical"}, AxesLabel -> {r}]

異なる辺補正メソッドを比較する：

Wolfram Language code: region = Ball[{0, 0, 0}]; pts = RandomPoint[region, 1000];

対相関関数の値を異なる3つのメソッドで推定する：

Wolfram Language code: rlist = Range[0.02, 0.5, 0.02]; mths = {"None", "BorderMargin", "Ripley"};
Wolfram Language code: data = PairCorrelationG[{pts, region}, rlist, SpatialBoundaryCorrection -> #]& /@ mths;

結果を可視化する：

Wolfram Language code: Show[Plot[1, {r, 0, Max[rlist]}, PlotStyle -> Gray, PlotLegends -> {"theoretical"}], ListPlot[data, DataRange -> MinMax[rlist], PlotLegends -> mths], AxesLabel -> {r}]

特性と関係  (1)

対相関関数をRipleyの 関数から推定する：

Wolfram Language code: reg = Disk[]; pts = RandomPoint[reg, 10 ^ 3];

データからの対相関：

Wolfram Language code: rlist = Range[0.01, 0.2, 0.01];
Wolfram Language code: pc = PairCorrelationG[{pts, reg}, rlist];

Ripleyの 関数を計算する：

Wolfram Language code: ripleyK = RipleyK[pts]

対相関を推定する：

Wolfram Language code: pcK = PairCorrelationG[{ripleyK, {0, 0.2, 0.01}}, rlist];

推定をデータから計算した対相関と比較する：

Wolfram Language code: ListLinePlot[{pc, pcK}, DataRange -> MinMax@rlist, PlotLegends -> {"PC from data", "PC estimated from K"}, AxesLabel -> {r}]

Besagの 関数を使っても同じ推定が得られる：

Wolfram Language code: besagL = BesagL[pts]; pcL = PairCorrelationG[{besagL, {0, 0.2, 0.01}}, rlist];
Wolfram Language code: MinMax[pcK - pcL]//Chop
Wolfram Research (2020), PairCorrelationG, Wolfram言語関数， https://reference.wolfram.com/language/ref/PairCorrelationG.html.

テキスト

Wolfram Research (2020), PairCorrelationG, Wolfram言語関数， https://reference.wolfram.com/language/ref/PairCorrelationG.html.

CMS

Wolfram Language. 2020. "PairCorrelationG." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PairCorrelationG.html.

APA

Wolfram Language. (2020). PairCorrelationG. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PairCorrelationG.html

BibTeX

@misc{reference.wolfram_2026_paircorrelationg, author="Wolfram Research", title="{PairCorrelationG}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PairCorrelationG.html}", note=[Accessed: 09-July-2026]}

BibLaTeX

@online{reference.wolfram_2026_paircorrelationg, organization={Wolfram Research}, title={PairCorrelationG}, year={2020}, url={https://reference.wolfram.com/language/ref/PairCorrelationG.html}, note=[Accessed: 09-July-2026]}