PenttinenPointProcess

PenttinenPointProcess[μ,γ,rp,d]

represents a Penttinen point process with constant intensity μ, interaction parameter γ and interaction radius rp in .

Details

  • PenttinenPointProcess is also known as pairwise area interaction process.
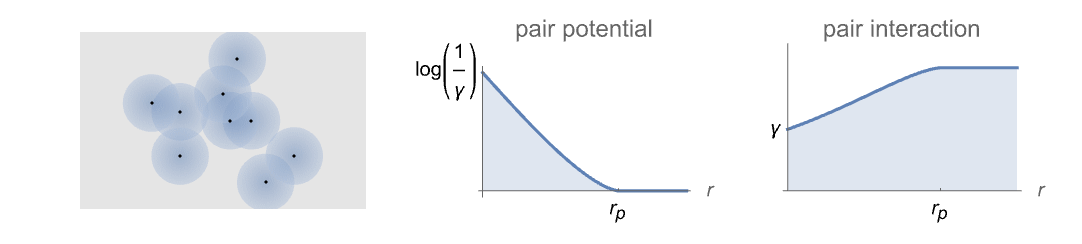
  • PenttinenPointProcess models point configurations where points have a pairwise repulsion that is log-linear in the measure of the overlap between balls around the points of radius rp, which are otherwise uniformly distributed.
  • The Penttinen model is typically used when the process interaction depends on the amount of shared resources within radius rp, such as plants, trees and nests of animals.
  • The Penttinen point process can be defined as a GibbsPointProcess in terms of its intensity μ and the pair potential ϕ or pair interaction h, which are both parametrized by γ and rp as follows:
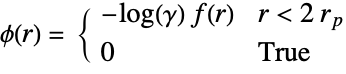
  • pair potential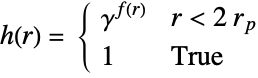
    pair interaction
  • Here 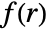is the measure of overlapping balls:
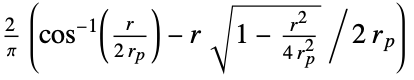
  • overlapping area in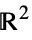
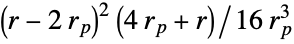
    overlapping volume in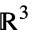
    1-r TemplateBox[{{{d, /, 2}, +, 1}}, Gamma] TemplateBox[{{1, /, 2}, {{(, {1, -, d}, )}, /, 2}, {3, /, 2}, {{(, {r, ^, 2}, )}, /, {(, {4, , {{r, _, p}, ^, 2}}, )}}}, Hypergeometric2F1]/(sqrt(pi) r_p TemplateBox[{{{(, {d, +, 1}, )}, /, 2}}, Gamma])overlapping measure in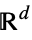
  • A point configuration from a Penttinen point process in an observation region reg has density function 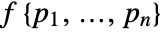proportional to mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm]), with respect to PoissonPointProcess[1,d].
  • The Papangelou conditional density 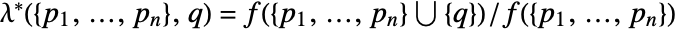for adding a point 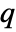to a point configuration is mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm]).
  • PenttinenPointProcess allows μ, γ and rp to be positive numbers such that 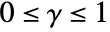, and d to be any positive integer.
  • PenttinenPointProcess simplifies to PoissonPointProcess when 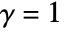. Smaller values of 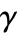gamma inhibit points within r_(p).
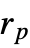  • Possible Method settings in RandomPointConfiguration for StraussPointProcess are:
  • "MCMC"Markov chain Monte Carlo birth and death
    "Exact"coupling from the past
  • Possible PointProcessEstimator settings in EstimatedPointProcess for PenttinenPointProcess are:
  • Automaticautomatically choose the parameter estimator
    "MaximumPseudoLikelihood"maximize the pseudo-likelihood
  • PenttinenPointProcess can be used with such functions as RipleyK and RandomPointConfiguration.

Examples

open allclose all

Basic Examples  (2)

Sample from a Penttinen point process:

Visualize the points in the sample:

Sample from a Penttinen point process defined on the surface of the Earth:

Visualize the points:

Scope  (2)

Generate three realizations from a Penttinen point process:

Estimate the parameters:

Generate three realizations from a Penttinen point process on the surface of the Earth:

Visualize the point configurations:

Estimate the parameters:

Options  (3)

Method  (3)

Sample using the Markov chain Monte Carlo method:

Specify the number of recursive calls to the sampler:

Specify the length of run:

Provide an initial state for the simulation:

Sample using an exact method:

Visualize the points in the sample:

Possible Issues  (1)

By default, the simulation will run until the number of points converges to a steady state, or until the default number of iterations is reached:

Raise the number of recursive calls to the sampler:

Specify a larger length of run:

Wolfram Research (2020), PenttinenPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/PenttinenPointProcess.html.

Text

Wolfram Research (2020), PenttinenPointProcess, Wolfram Language function, https://reference.wolfram.com/language/ref/PenttinenPointProcess.html.

CMS

Wolfram Language. 2020. "PenttinenPointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PenttinenPointProcess.html.

APA

Wolfram Language. (2020). PenttinenPointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PenttinenPointProcess.html

BibTeX

@misc{reference.wolfram_2024_penttinenpointprocess, author="Wolfram Research", title="{PenttinenPointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PenttinenPointProcess.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_penttinenpointprocess, organization={Wolfram Research}, title={PenttinenPointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/PenttinenPointProcess.html}, note=[Accessed: 18-November-2024 ]}