PlanarAngle

PlanarAngle[p{q1,q2}]

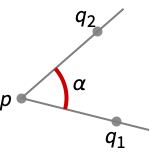
p からの q1を通る半直線と q2を通る半直線の間の角である．

PlanarAngle[{q1,p,q2}]

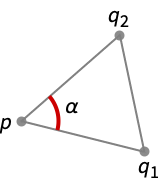
頂点 p，q1，q2の三角形で形成された点 p における角を与える．

PlanarAngle[…,"spec"]

"spec"で指定された角を与える．

詳細

  • PlanarAngleは角度としても知られている．
  • PlanarAngle[p{q1,q2}]は，p から左に q1までと p から右に q2までの半直線で定義された単位円Circle[p]の弧長を与える．
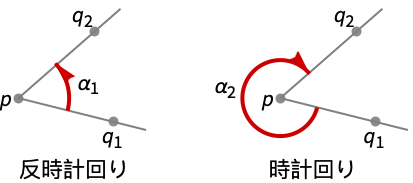
  • p から q1までと p から q2までの2本の半直線は，2つの角 α1と α2を p で分割する．
  • 次の指定"spec"を使うことができる．
  • "Counterclockwise"q1から q2まで反時計回りで形成される角度
    "Clockwise"q1から q2まで時計回りで形成される角度
  • PlanarAngle[p{q1,q2},"Counterclockwise"]はPlanarAngle[p{q1,q2}]に等しい．
  • PlanarAngle[p{q1,q2},"Clockwise"]はPlanarAngle[p{q2,q1}]に等しい．
  • PlanarAngle[{q1,p,q2}]は，p からの線分 q1 q2に対する角である．
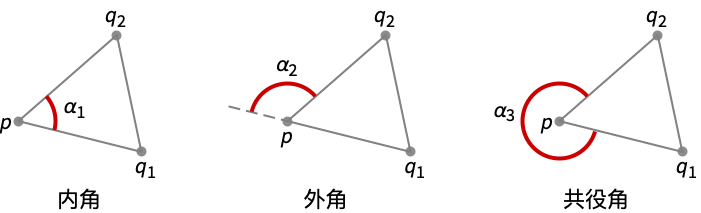
  • 頂点 q1，p，q2を持つ三角形は p における3つの角 α1，α2，α3を定義する．
  • 次は，使用可能な指定"spec"である．
  • "Interior"p における三角形の内角
    "Exterior"p における三角形の外角
    "FullExterior"p における三角形の共役角
  • PlanarAngle[{q1,p,q2},"Interior"]はPlanarAngle[{q1,p,q2}]に等しい．
  • PlanarAngle[{q1,p,q2},"Exterior"]は π-PlanarAngle[{q1,p,q2}]に等しい．
  • PlanarAngle[{q1,p,q2},"FullExterior"]は2π-PlanarAngle[{q1,p,q2}]に等しい．
  • "Interior"，"Exterior"あるいは"FullExterior"の指定のとき，PlanarAngle[p{q1,q2},"spec"]はPlanarAngle[{q1,p,q2},"spec"]と解釈される．
  • 指定"Counterclockwise"または"Clockwise"のとき，PlanarAngle[{q1,p,q2},"spec"]はPlanarAngle[p{q1,q2}, "spec"]であると解釈される．
  • PlanarAngleはGeometricSceneの記号による点とともに使うことができる．

例題

すべて開くすべて閉じる

例  (2)

{0,0}からの{1,1}と{1,0}を通る半直線間の角度：

原点における三角形で形成された角度：

スコープ  (7)

基本的用法  (2)

PlanarAngleを使って2本の半直線間の角度を求める：

PlanarAngleは数値引数に使うことができる：

記号引数：

指定  (5)

"Counterclockwise"  (1)

反時計回りの回転で形成された角：

"Clockwise"  (1)

時計回りの回転で形成された角：

"Interior"  (1)

原点における三角形の内角：

"Exterior"  (1)

原点における三角形の外角：

"FullExterior"  (1)

原点における三角形の共役角：

アプリケーション  (6)

平角：

これは π の角である：

鈍角：

これは から π までの角である：

直角：

これは の角である：

鋭角：

これは より小さい角である：

点 p における三角形の内角を求める：

AASTriangle：

角度を得る：

特性と関係  (7)

PlanarAngle[p,{q2,q1}]は2π-PlanarAngle[p,{q1,q2}]に等しい：

PlanarAngle[{q1,p,q2},"Interior"]は p の周りの回転によって形成される最小の角である：

PlanarAngle[p{q1,q2}]は0から2π までの値を取る：

PlanarAngle[{q1,p,q2}]は0から π までの値を取る：

二面角は，法線 p2-p1と点 p1で定義される平面上の平面角である：

PlanarAngle[p->{q1,q2}]はPolygonAngle[ℛ, p]に等しい．ただし，q1および q2は多面体 ℛ 内の p の隣接点である：

PlanarAngle[{q1,p,q2}]はSolidAngle[p,{q1,q2}に等しい：

考えられる問題  (1)

PlanarAngleは記号パラメータについての一般的な値を与える：

Wolfram Research (2019), PlanarAngle, Wolfram言語関数， https://reference.wolfram.com/language/ref/PlanarAngle.html.

テキスト

Wolfram Research (2019), PlanarAngle, Wolfram言語関数， https://reference.wolfram.com/language/ref/PlanarAngle.html.

CMS

Wolfram Language. 2019. "PlanarAngle." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PlanarAngle.html.

APA

Wolfram Language. (2019). PlanarAngle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PlanarAngle.html

BibTeX

@misc{reference.wolfram_2024_planarangle, author="Wolfram Research", title="{PlanarAngle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/PlanarAngle.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_planarangle, organization={Wolfram Research}, title={PlanarAngle}, year={2019}, url={https://reference.wolfram.com/language/ref/PlanarAngle.html}, note=[Accessed: 22-November-2024 ]}