WOLFRAM

Wolfram 语言与系统参考资料中心

PlanarAngle[p{q1,q2}]

给出从 p 到 q1 和 q2 的半直线之间的角度.

PlanarAngle[{q1,p,q2}]

给出由顶点 p、q1 和 q2 构成的三角形在 p 形成的角.

PlanarAngle[…,"spec"]

给出由 "spec" 指定的角.

更多信息
Details and Options Details and Options
范例  
基本范例  
范围  
基本用法  
指定  
"Counterclockwise"  
"Clockwise"  
"Interior"  
"Exterior"  
"FullExterior"  
应用  
属性和关系  
可能存在的问题  
参见
相关指南
历史
按以下格式引用：

PlanarAngle

PlanarAngle[p{q1,q2}]

给出从 p 到 q1 和 q2 的半直线之间的角度.

PlanarAngle[{q1,p,q2}]

给出由顶点 p、q1 和 q2 构成的三角形在 p 形成的角.

PlanarAngle[…,"spec"]

给出由 "spec" 指定的角.

更多信息

  • PlanarAngle 亦称为角.
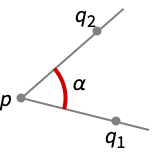
  • PlanarAngle[p{q1,q2}] 给出单位圆 Circle[p] 上由左边从 p 到 q1 的半线和右边从 p 到 q2 的半线限定的弧的长度.
  • 从 p 到 q1 和 q2 的两条半直线限定了 p 处的两个角 α1 和 α2.
  • 可给出以下指定 "spec"：
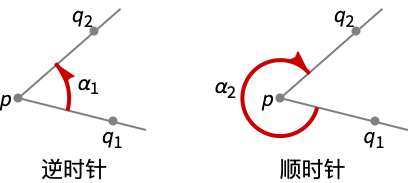
  • "Counterclockwise"从 q1 到 q2 逆时针旋转形成的角
    "Clockwise"从 q1 到 q2 顺时针旋转形成的角
  • PlanarAngle[p{q1,q2},"Counterclockwise"] 等价于 PlanarAngle[p{q1,q2}].
  • PlanarAngle[p{q1,q2},"Clockwise"] 等价于 PlanarAngle[p{q2,q1}].
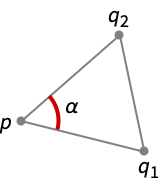
  • PlanarAngle[{q1,p,q2}] 是从 p 到 q1 和 q2 的线段所对应的角度.
  • 由顶点 q1、p 和 q2 构成的三角形定义了 p 处的三个角 α1、α2 和 α3.
  • 可给出以下指定 "spec"：
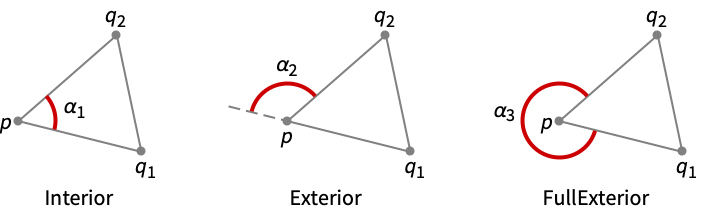
  • "Interior"三角形在 p 处的内角
    "Exterior"三角形在 p 处的外角
    "FullExterior"三角形在 p 处的全外角
  • PlanarAngle[{q1,p,q2},"Interior"] 等价于 PlanarAngle[{q1,p,q2}].
  • PlanarAngle[{q1,p,q2},"Exterior"] 等价于 π-PlanarAngle[{q1,p,q2}].
  • PlanarAngle[{q1,p,q2},"FullExterior"] 等价于 2π-PlanarAngle[{q1,p,q2}].
  • 当给出指定 "Interior"、"Exterior" 或 "FullExterior" 时，PlanarAngle[p{q1,q2},"spec"] 被认为是 PlanarAngle[{q1,p,q2},"spec"].
  • 当给出指定 "Counterclockwise" 或 "Clockwise" 时，PlanarAngle[{q1,p,q2},"spec"] 被认为是 PlanarAngle[p{q1,q2}, "spec"].
  • PlanarAngle 可与符号点一起在 GeometricScene 中使用.

范例

打开所有单元 关闭所有单元

基本范例  (2)

从 {0,0} 到 {1,1} 和 {1,0} 的半直线之间的角：

Wolfram Language code: PlanarAngle[{0, 0} -> {{1, 0}, {1, 1}}]
Wolfram Language code: Graphics[{Arrow[{{0, 0}, {1, 0}}], Arrow[{{0, 0}, {1, 1}}]}]

在原点处的三角形形成的角：

Wolfram Language code: PlanarAngle[{{0, 1}, {0, 0}, {1, 0}}]
Wolfram Language code: Graphics[Triangle[{{0, 1}, {0, 0}, {1, 0}}]]

范围  (7)

基本用法  (2)

用 PlanarAngle 求两条半直线之间的角：

Wolfram Language code: PlanarAngle[{0, 0} -> {{1, 0}, {1, 1}}]
Wolfram Language code: Graphics[{HalfLine[{0, 0}, {1, 0}], HalfLine[{0, 0}, {1, 1}]}]

PlanarAngle 适用于数值参数：

Wolfram Language code: PlanarAngle[{0, 0} -> {{1, 0}, {1, 1}}]

符号参数：

Wolfram Language code: PlanarAngle[{0, 0} -> {{0, 1}, {1, a}}]

指定  (5)

"Counterclockwise"  (1)

逆时针旋转形成的角：

Wolfram Language code: PlanarAngle[{0, 0} -> {{1, 0}, {1, 1}}, "Counterclockwise"]
Wolfram Language code: Graphics[{Arrowheads[0.1], Arrow[{{{0, 0}, {1, 0}}, {{0, 0}, {1, 1}}}]}]

"Clockwise"  (1)

顺时针旋转形成的角：

Wolfram Language code: PlanarAngle[{0, 0} -> {{1, 0}, {1, 1}}, "Clockwise"]
Wolfram Language code: Graphics[{Arrowheads[0.1], Arrow[{{{0, 0}, {1, 0}}, {{0, 0}, {1, 1}}}]}]

"Interior"  (1)

三角形在原点处的内角：

Wolfram Language code: PlanarAngle[{{1, 1}, {0, 0}, {1, 0}}, "Interior"]
Wolfram Language code: Graphics[{FaceForm[], EdgeForm[StandardGray], Triangle[{{1, 1}, {0, 0}, {1, 0}}]}]

"Exterior"  (1)

三角形在原点处的外角：

Wolfram Language code: PlanarAngle[{{1, 1}, {0, 0}, {1, 0}}, "Exterior"]
Wolfram Language code: Graphics[{FaceForm[], EdgeForm[StandardGray], Triangle[{{1, 1}, {0, 0}, {1, 0}}]}]

"FullExterior"  (1)

三角形在原点处的全外角：

Wolfram Language code: PlanarAngle[{{1, 1}, {0, 0}, {1, 0}}, "FullExterior"]
Wolfram Language code: Graphics[{FaceForm[], EdgeForm[StandardGray], Triangle[{{1, 1}, {0, 0}, {1, 0}}]}]

应用  (6)

平角：

Wolfram Language code: p = {0, 0};q1 = {1, 0};q2 = {-1, 0};
Wolfram Language code: Graphics[{Arrow[{{p, q1}, {p, q2}}], Point[p]}]

是角度为 π 的角：

Wolfram Language code: PlanarAngle[p -> {q1, q2}]

钝角：

Wolfram Language code: p = {0, 0};q1 = {1, 0};q2 = {-1, 1};
Wolfram Language code: Graphics[{Arrow[{{p, q1}, {p, q2}}], Point[p]}]

是角度在 和 π 之间的角：

Wolfram Language code: PlanarAngle[p -> {q1, q2}]

直角：

Wolfram Language code: p = {0, 0};q1 = {1, 0};q2 = {0, 1};
Wolfram Language code: Graphics[{Arrow[{{p, q1}, {p, q2}}], Point[p]}]

是角度为 的角：

Wolfram Language code: PlanarAngle[p -> {q1, q2}]

锐角：

Wolfram Language code: p = {0, 0};q1 = {1, 0};q2 = {1, 1};
Wolfram Language code: Graphics[{Arrow[{{p, q1}, {p, q2}}], Point[p]}]

是角度小于 的角：

Wolfram Language code: PlanarAngle[p -> {q1, q2}]

求三角形在点 p 处的内角：

Wolfram Language code: p = {0, 0};q1 = {2, 0};q2 = {1, 1};
Wolfram Language code: ℛ = Triangle[{p, q1, q2}];
Wolfram Language code: Graphics[ℛ]
Wolfram Language code: PlanarAngle[p -> {q1, q2}]

一个 AASTriangle：

Wolfram Language code: AASTriangle[Pi / 6, Pi / 3, 1]
Wolfram Language code: Graphics[%]

获取角度：

Wolfram Language code: PlanarAngle[{0, 0} -> {{2, 0}, {(3/2), (Sqrt[3]/2)}}]
Wolfram Language code: PlanarAngle[{2, 0} -> {{(3/2), (Sqrt[3]/2)}, {0, 0}}]
Wolfram Language code: PlanarAngle[{(3/2), (Sqrt[3]/2)} -> {{0, 0}, {2, 0}}]

属性和关系  (7)

PlanarAngle[p,{q2,q1}] 等于 2π-PlanarAngle[p,{q1,q2}]:

Wolfram Language code: PlanarAngle[{2, 1} -> {{1, 1}, {1, 0}}]
Wolfram Language code: 2Pi - PlanarAngle[{2, 1} -> {{1, 0}, {1, 1}}]

PlanarAngle[{q1,p,q2},"Interior"] 是绕 p 旋转形成的最小的角：

Wolfram Language code: PlanarAngle[{{1, 1}, {2, 1}, {1, 0}}, "Interior"]
Wolfram Language code: Min[PlanarAngle[{2, 1} -> {{1, 1}, {1, 0}}, #]& /@ {"Counterclockwise", "Clockwise"}]

PlanarAngle[p{q1,q2}] 取从 0 到 2π 的值：

Wolfram Language code: Table[PlanarAngle[{0, 0} -> {{1, 0}, p}], {p, CirclePoints[{1, 0}, 12]}]

PlanarAngle[{q1,p,q2}] 取从 0 到 π 的值：

Wolfram Language code: Table[PlanarAngle[{{1, 0}, {0, 0}, p}], {p, CirclePoints[{1, 0}, 12]}]

二面角是由法线 p2-p1 和点 p1 定义的平面上的平面角：

Wolfram Language code: p1 = {0, 0, 0};p2 = {0, 0, 1}; v = {1, 0, 0};w = {0, 1, 0};
Wolfram Language code: DihedralAngle[{p1, p2}, {v, w}]
Wolfram Language code: PlanarAngle[p1[[1 ;; 2]] -> {v[[1 ;; 2]], w[[1 ;; 2]]}]

PlanarAngle[p->{q1,q2}] 等价于 PolygonAngle[ℛ, p]，其中 q1 和 q2 是多边形 ℛ 中 p 的相邻点：

Wolfram Language code: ℛ = Polygon[{{1., 0.}, {0.5, 0.8}, {-0.5, 0.8}, {-1., 0.}}]
Wolfram Language code: PolygonAngle[ℛ, {0.5, 0.8}]
Wolfram Language code: PlanarAngle[{0.5, 0.8} -> {{-0.5, 0.8}, {1., 0.}}]

PlanarAngle[{q1,p,q2}] 等价于 SolidAngle[p,{q1,q2}]：

Wolfram Language code: PlanarAngle[{{1, 0}, {0, 0}, {1, 1}}]
Wolfram Language code: SolidAngle[{0, 0}, {{1, 0}, {1, 1}}]
Wolfram Language code: Graphics[Arrow[{{0, 0}, #}]& /@ {{1, 0}, {1, 1}}]

可能存在的问题  (1)

对于符号参数，PlanarAngle 给出通用值：

Wolfram Language code: PlanarAngle[{0, 0} -> {{1, 0}, {0, a}}]
Wolfram Research (2019)，PlanarAngle，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PlanarAngle.html.

文本

Wolfram Research (2019)，PlanarAngle，Wolfram 语言函数，https://reference.wolfram.com/language/ref/PlanarAngle.html.

CMS

Wolfram 语言. 2019. "PlanarAngle." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PlanarAngle.html.

APA

Wolfram 语言. (2019). PlanarAngle. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PlanarAngle.html 年

BibTeX

@misc{reference.wolfram_2026_planarangle, author="Wolfram Research", title="{PlanarAngle}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/PlanarAngle.html}", note=[Accessed: 06-September-2026]}

BibLaTeX

@online{reference.wolfram_2026_planarangle, organization={Wolfram Research}, title={PlanarAngle}, year={2019}, url={https://reference.wolfram.com/language/ref/PlanarAngle.html}, note=[Accessed: 06-September-2026]}