PointDensity

PointDensity[pdata]

estimates the point density function from point data pdata.

PointDensity[pdata,pmethod]

estimates the point density function with the partition method pmethod.

PointDensity[bdata,…]

estimates the point density function from binned data bdata.

PointDensity[pproc,…]

computes the density function for point process pproc.

Details and Options

  • Point density is also known as point intensity.
  • The point density 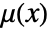gives a function that describes how the number of points 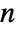varies per length, area and volume in the observation region ℛ. The integral over the region is the total number of points .
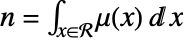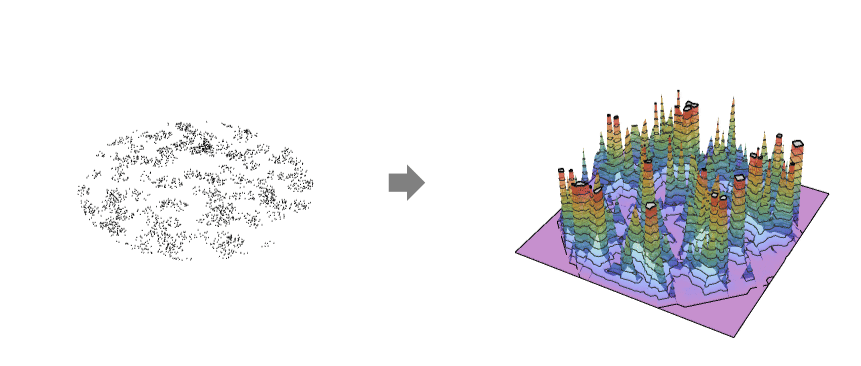
  • PointDensity gives a partition-based estimator that adapts to the point collection in how the partition is formed, effectively using a cell per point.
  • The resulting point density function typically looks very noisy. To get a smoothed version of the point density, use HistogramPointDensity or SmoothPointDensity.
  • Point density is typically used to define an inhomogeneous Poisson process or a measure of inhomogeneity.
  • PointDensity returns a PointDensityFunction that can be used to evaluate the density function repeatedly.
  • The point data pdata can have the following forms:
  • {p1,p2,…}points pi
    GeoPosition[…],GeoPositionXYZ[…],…geographic points
    SpatialPointData[…]spatial point collection
    {pts,reg}point collection pts and observation region reg
  • If the observation region reg is not given, a region automatically computed using RipleyRassonRegion.
  • For the point intensity estimation from the binned data bdata, which is assumed to be SpatialBinnedPointData, the points are simulated uniformly in each bin.
  • The point process pproc can have the following forms:
  • proca point process proc with exact formulas
    {proc,reg}a point process proc and observation region reg based on simulation
  • The observation region reg should be a parameter-free, full-dimensional and bounded region as tested by SpatialObservationRegionQ.
  • The partition method pmethod can be used:
  • "Delaunay"Delaunay cells from point data; gives a piecewise linear density function (default)
    "Voronoi"Voronoi cells from point data; gives a piecewise-constant density function
    {"Voronoi",n}aggregate cells so that approximately n cells remain, based on the smallest cells first

Examples

open allclose all

Basic Examples  (3)

Create a SpatialPointData:

Plot the points:

Estimate the point intensity:

Value at a point:

Visualize the intensity estimation:

Calculate PointDensity on the surface of the Earth:

Visualize the density function using random locations:

Create density for an InhomogeneousPoissonPointProcess from data:

Compute the point intensity function:

Define an InhomogeneousPoissonPointProcess with the computed point density:

Sample from this point process:

Scope  (7)

Point Data  (4)

Create a homogeneous univariate SpatialPointData:

Compute the point intensity function using different partition methods:

Visualize using a random point sample:

Create an inhomogeneous univariate SpatialPointData:

Compare the point density function with the smooth kernel density method:

Visualize:

The point density of clustered data:

Compute the point density from data:

Visualize:

Point the density for a hardcore process:

Compute the point density:

Visualize:

Point Processes  (3)

The point density function for PoissonPointProcess is constant in every dimension:

The point density function for InhomogeneousPoissonPointProcess:

The point density function for BinomialPointProcess on a ball:

In 1D:

In 2D:

In 3D:

For a process defined on a square:

Properties & Relations  (1)

The density integrates to the number of points:

Wolfram Research (2020), PointDensity, Wolfram Language function, https://reference.wolfram.com/language/ref/PointDensity.html.

Text

Wolfram Research (2020), PointDensity, Wolfram Language function, https://reference.wolfram.com/language/ref/PointDensity.html.

CMS

Wolfram Language. 2020. "PointDensity." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PointDensity.html.

APA

Wolfram Language. (2020). PointDensity. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PointDensity.html

BibTeX

@misc{reference.wolfram_2024_pointdensity, author="Wolfram Research", title="{PointDensity}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/PointDensity.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_pointdensity, organization={Wolfram Research}, title={PointDensity}, year={2020}, url={https://reference.wolfram.com/language/ref/PointDensity.html}, note=[Accessed: 18-November-2024 ]}