PoissonPointProcess
PoissonPointProcess[μ,d]
表示 ![]() 中的一个具有恒定强度 μ 的齐次泊松点过程.
中的一个具有恒定强度 μ 的齐次泊松点过程.
更多信息

- PoissonPointProcess 亦称为齐次泊松点过程、平稳泊松点过程和完全空间随机性 (CSR).
- PoissonPointProcess 生成均匀分布在一个区域中的点,每单位体积的平均点数等于 μ.
-
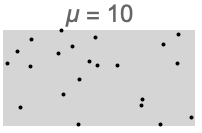
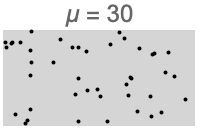

- 常见用途是对空间上完全随机的点集进行建模和测试. 通过被用作构建更复杂的点过程(如聚类点过程)的基块.
- 强度为 μ 时,体积为
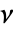 的观察区域中的点数服从分布 PoissonDistribution[μ ν].
的观察区域中的点数服从分布 PoissonDistribution[μ ν]. - 对于泊松点过程,不相交区域
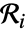 中的点数
中的点数 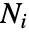 由使得
由使得 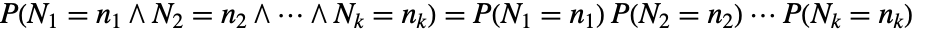 成立的独立随机变量组成. 此属性也称为完全空间随机性(CSR).
成立的独立随机变量组成. 此属性也称为完全空间随机性(CSR). - 关于 PoissonPointProcess[1,d],体积为
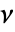 的观察区域
的观察区域 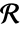 中强度为 μ 的点布局
中强度为 μ 的点布局  的密度函数为
的密度函数为 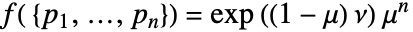 .
. - 对于强度为 μ 的泊松点过程,将点
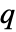 添加到点布局
添加到点布局  的 Papangelou 条件密度
的 Papangelou 条件密度 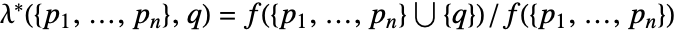 为
为 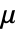 .
. - PoissonPointProcess 允许 μ 为任意正实数,允许 d 为任意正整数.
- PoissonPointProcess 的 EstimatedPointProcess 中可能的 PointProcessEstimator 的设置为:
-
Automatic 自动选择参数估计器 "MaximumPseudoLikelihood" 最大化伪似然 - PoissonPointProcess 可与诸如 RipleyK 和 RandomPointConfiguration 这样的函数一起使用.
范例
打开所有单元关闭所有单元范围 (4)
对来自任何有效区域(其 RegionEmbeddingDimension 等于它的 RegionDimension)的泊松点过程进行采样:
来自使用不同方法生成的 PoissonPointProcess 的样本:
估计地理区域上的 PoissonPointProcess:
应用 (3)
属性和关系 (11)
PoissonPointProcess 中的点数服从泊松分布:
模拟单位圆盘上的 PoissonPointProcess:
将点数拟合为 PoissonDistribution:
这等于 RayleighDistribution 的 CDF:
也相当于在 PointCountDistribution 的 0 处计算 SurvivalFunction:
PoissonPointProcess 具有完全空间随机性:
泊松点过程的 Ripley's ![]() 函数有解析形式,与强度无关:
函数有解析形式,与强度无关:
泊松点过程的 PairCorrelationG 是恒定的:
泊松点过程的 EmptySpaceF 和 NearestNeighborG 函数是一样的:
它们都相当于 ExponentialDistribution 的 CDF:
强度恒定的 InhomogeneousPoissonPointProcess 是 PoissonPointProcess:
文本
Wolfram Research (2020),PoissonPointProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/PoissonPointProcess.html.
CMS
Wolfram 语言. 2020. "PoissonPointProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/PoissonPointProcess.html.
APA
Wolfram 语言. (2020). PoissonPointProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/PoissonPointProcess.html 年