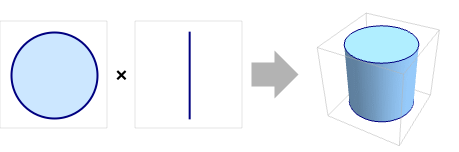
RegionProduct

RegionProduct[reg1,reg2]

代表区域 reg1 和 reg2 的笛卡儿积.

RegionProduct[reg1,reg2,…]

代表区域 reg1, reg2, … 的笛卡儿积.

更多信息

  • RegionProduct 又被称为外积区域.
  • RegionProduct[reg1,reg2] 代表区域 .
  • 乘积区域的嵌入维数是输入嵌入维数之和，几何维数则是几何维数之和.

范例

打开所有单元关闭所有单元

基本范例  (3)

两条线段的积：

可视化：

一个圆盘和一条线段的积：

可视化：

两个 BoundaryMeshRegion 对象的积：

范围  (7)

公式范围  (3)

在一维的一个 ImplicitRegion 和一个 ParametricRegion 的积：

计算它的 Area：

可视化：

两个 ImplicitRegion 对象的积：

该区域无界，所以它的体积无限大：

两个 ParametricRegion 对象的积：

计算它的 Volume：

网格区域  (4)

两个在一维的 BoundaryMeshRegion 对象的积：

结果是一个 MeshRegion，而不是 BoundaryMeshRegion：

在一维的两个 MeshRegion 对象的积：

计算 Area：

一维和二维 BoundaryMeshRegion 对象的积：

计算 Volume：

一维和二维 MeshRegion 对象的积：

计算 Volume：

应用  (2)

定义一个张量积网格为几个一维网格的积：

根据一系列点定义一维网格：

定义二维张量积网格：

定义三维张量积网格：

直接构建 MeshRegion，用来表示康托集的某一级. 从区间 {0,1} 开始，每一步去掉中间的三分之一：

最开始的几步：

用 RegionProduct 来生成康托尘埃：

求康托集每一步的长度：

估计通用公式：

求二维康托集每一步的度量：

求三维康托集每一步的度量：

属性和关系  (10)

积的 RegionEmbeddingDimension 是其输入嵌入维数的和：

积的 RegionDimension 是输入维数的和：

特殊区域的 RegionProduct 被留下未做计算：

它是一个区域，可被用来做计算：

公式区域的 RegionProduct 被留下未做计算：

它是一个区域，可被用来做计算：

MeshRegion 或 BoundaryMeshRegion 对象的积本身是一个 MeshRegion：

积的 RegionMeasure 是输入测度的积：

积的 RegionCentroid 是输入的几何中心结合在一起：

一个 Rectangle 是两个 Line 对象的积：

证明隶属度是相当的：

一个 Cuboid 是三个 Line 对象的积：

证明隶属度是相当的：

Cylinder 是一个 Disk 和一条 Line 的积：

证明隶属度是相当的：

巧妙范例  (1)

将康托尔尘状区域定义为康托尔集的积:

在二维的康托尔集的积：

在三维的康托尔集的积：

Wolfram Research (2014)，RegionProduct，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RegionProduct.html.

文本

Wolfram Research (2014)，RegionProduct，Wolfram 语言函数，https://reference.wolfram.com/language/ref/RegionProduct.html.

CMS

Wolfram 语言. 2014. "RegionProduct." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/RegionProduct.html.

APA

Wolfram 语言. (2014). RegionProduct. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/RegionProduct.html 年

BibTeX

@misc{reference.wolfram_2024_regionproduct, author="Wolfram Research", title="{RegionProduct}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RegionProduct.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_regionproduct, organization={Wolfram Research}, title={RegionProduct}, year={2014}, url={https://reference.wolfram.com/language/ref/RegionProduct.html}, note=[Accessed: 05-November-2024 ]}