SechDistribution

SechDistribution[μ,σ]

位置母数 μ，尺度母数 σ の双曲線正割分布を表す．

SechDistribution[]

位置母数0，尺度母数1の双曲線正割分布を表す．

詳細

  • 双曲線正割分布における値 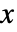の確率密度は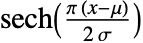に比例する．
  • SechDistributionでは，μ は任意の実数でよく，σ は任意の正の実数でよい．
  • SechDistributionでは，μ と σ は単位次元が等しい任意の数量でよい． »
  • SechDistributionは，Mean，CDF，RandomVariate等の関数とともに使うことができる．

予備知識

  • SechDistribution[μ,σ]は，実数集合上で定義されサポートされており，実数 μ（「位置母数」と呼ばれる）および正の実数 σ（「尺度母数」と呼ばれる）でパラメータ化された連続統計分布を表す．これらの母数は，ともに，確率密度関数(PDF)の全体的な動作を決定する．一般に，双曲線正割分布のPDFはベル型で単一の「峰」（大域的最大値）を持つ単峰性であるが，その全体的な形（高さ，広がり，最大値の水平位置）は μ と σ の値で決定される．加えて，PDFの裾部は，PDFが 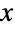の大きい値について代数的というよりむしろ指数的に減少するという意味で「薄い」（この動作は分布のSurvivalFunctionを分析することで数量的に厳密にすることができる）．母数のない形のSechDistribution[]はSechDistribution[0,1]に等しく，標準双曲線正割分布と呼ばれることがある．
  • 双曲線正割分布の包括的な研究は，J. Talackoによる，いわゆるパークスの分布の研究の一部として，この分布がロジシティック分布(LogisticDistribution) の特殊ケースとして分離された1950年代に始まったようである．双曲線正割分布には，モデリング，回帰，推論等を含む，統計的にさまざまな用法があり，その萌芽期より，収入分布，電気通信における偏光光学，ある種の銀河構造モデルにおける惑星数等の数多くの現象モデル化に使われている．
  • RandomVariateを使って，双曲線正割分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,SechDistribution[μ,σ]]（より簡略な表記では xSechDistribution[μ,σ]）を使って，確率変数 x が双曲線正割分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 双曲線正割分布の確率密度関数および累積分布関数は，PDF[SechDistribution[μ,σ],x]およびCDF[SechDistribution[μ,σ],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合が双曲線正割分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリック双曲線正割分布を推定することが，FindDistributionParametersを使ってデータを双曲線正割分布にフィットすることができる．ProbabilityPlotを使って記号双曲線正割分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号双曲線正割分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換された双曲線正割分布を表すことが，CensoredDistributionを使って上限値と下限値の間で打ち切られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使って双曲線正割分布を含む高次元分布を構築することが，ProductDistributionを使って双曲線正割分布を含む独立成分分布の結合分布を計算することができる．
  • SechDistributionは他の数多くの分布と関連している．SechDistributionは，定性的には，これらすべてがベル型をしており，SechDistribution[μ,σ]，NormalDistribution[μ,σ]，LogisticDistribution[ 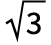σ/π]のそれぞれがMean μ およびVariance σ2を持つという意味で，NormalDistributionおよびLogisticDistributionと類似している．SechDistributionはCauchyDistribution の変換(TransformedDistribution)として得ることができ，SechDistribution[μ,σ]のPDFが厳密にMeixnerDistribution[2σ,0,μ,1/2]のそれと等しいという意味でMeixnerDistributionの特殊ケースである．SechDistributionはGompertzMakehamDistribution，FrechetDistribution，ParetoDistribution，WeibullDistribution，MaxStableDistribution，MinStableDistributionとも関連している．

例題

すべて開くすべて閉じる

例  (4)

確率密度関数：

累積分布関数：

平均と分散：

中央値：

スコープ  (7)

双曲線正割分布から擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度と尖度は一定である：

母数の関数としての閉形式の種々のモーメント：

Moment：

CentralMoment：

記号次数の閉形式：

FactorialMoment：

Cumulant：

記号次数の閉形式：

ハザード関数：

分位関数：

母数でQuantityを一貫して使うとQuantityDistributionが与えられる：

重さの平均を計算する：

アプリケーション  (2)

SechDistributionはソリトン波の包絡線である．半値全幅を求める：

平均と分散が等しい二変量正規分布に従う双子の特徴間の級内相関係数 の逆正接双曲線関数は，双曲線割線分布に従う：

級内相関係数は，平均 および分散 から独立している．かつ について係数の逆正接双曲線関数を定義する：

サンプルを取り，これがSechDistributionから取られたものであるかもしれないという
仮説を検定する：

QuantilePlotで適合度を調べる：

特性と関係  (6)

双曲線正割分布は平行移動と正の因子によるスケーリングの下では閉じている：

他の分布との関係：

SechDistributionはMeixnerDistributionの特殊ケースである：

SechDistributionはCauchyDistributionの関数変換で得ることができる：

双曲線正割分布についての式と比較する：

SechDistributionの確率密度関数は鐘型でNormalDistributionおよびLogisticDistributionに似ている：

SechDistributionの裾部はNormalDistributionやLogisticDistributionの裾部より重い：

3つの分布の平均と分散はすべて等しい：

SechDistributionはLogisticDistributionより尖度が大きい：

双曲線正割分布はLogisticDistributionに似ている：

双曲線正割分布をデータにフィットする：

そのヒストグラムと推定分布の確率密度関数を比較する：

ロジスティック分布をデータにフィットする：

尤度はほぼ等しい：

DistributionFitTestは，データが双曲線正割分布分布からのものであるという仮説を拒絶する：

おもしろい例題  (1)

累積分布関数の等高線を持つ σ のさまざまな値についての確率密度関数：

Wolfram Research (2010), SechDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/SechDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2010), SechDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/SechDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2010. "SechDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/SechDistribution.html.

APA

Wolfram Language. (2010). SechDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SechDistribution.html

BibTeX

@misc{reference.wolfram_2024_sechdistribution, author="Wolfram Research", title="{SechDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/SechDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_sechdistribution, organization={Wolfram Research}, title={SechDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/SechDistribution.html}, note=[Accessed: 22-November-2024 ]}