SinDegreesCopy to clipboard.
✖
SinDegrees
更多信息

- SinDegrees 和其他三角函数是在高中几何课程中学习的内容,在许多科学学科中也有应用.
- SinDegrees 的参数单位假定为度.
- 当 SinDegrees 的参数是
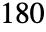 的简单有理倍数时,它会自动求值;对于更复杂的有理倍数,有时可以使用 FunctionExpand.
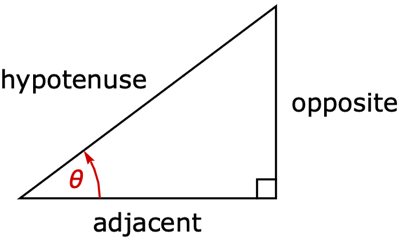
的简单有理倍数时,它会自动求值;对于更复杂的有理倍数,有时可以使用 FunctionExpand. - 角
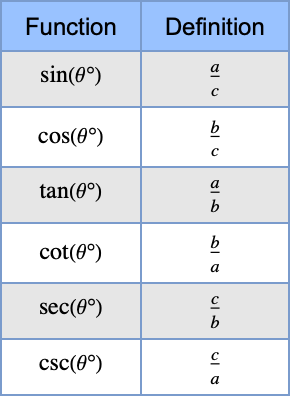
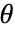 的 SinDegrees 是直角三角形对边与斜边的比值:
的 SinDegrees 是直角三角形对边与斜边的比值: - SinDegrees 与 CosDegrees 的关系通过毕达哥拉斯恒等式
![TemplateBox[{theta}, SinDegrees]^2+TemplateBox[{theta}, CosDegrees]^2=1 TemplateBox[{theta}, SinDegrees]^2+TemplateBox[{theta}, CosDegrees]^2=1](Files/SinDegrees.zh/4.png) 来展现.
来展现. - 对于某些特殊参数,SinDegrees 会自动求出精确值.
- SinDegrees 可以按照任意数值精度进行计算.
- SinDegrees 自动线性作用于列表.
- SinDegrees 可用于 Interval、CenteredInterval 和 Around 对象.
- 数学函数,适用于符号和数字运算.
范例
打开所有单元关闭所有单元基本范例 (6)常见实例总结
https://wolfram.com/xid/0pupqdhpkk-zvnbzt
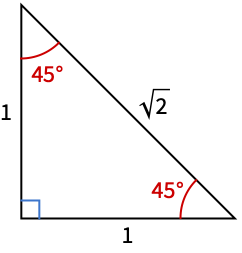
计算单位边长的直角三角形 45 度角的 SinDegrees:
https://wolfram.com/xid/0pupqdhpkk-8uoawe
https://wolfram.com/xid/0pupqdhpkk-yqnf8d
https://wolfram.com/xid/0pupqdhpkk-0yb4bb
https://wolfram.com/xid/0pupqdhpkk-m2b8vb
https://wolfram.com/xid/0pupqdhpkk-x15
https://wolfram.com/xid/0pupqdhpkk-8xz705
范围 (47)标准用法实例范围调查
数值运算 (6)
https://wolfram.com/xid/0pupqdhpkk-l274ju
https://wolfram.com/xid/0pupqdhpkk-b0wt9
https://wolfram.com/xid/0pupqdhpkk-xth5g
SinDegrees 可以接受复数输入:
https://wolfram.com/xid/0pupqdhpkk-hfml09
高精度高效运算 SinDegrees:
https://wolfram.com/xid/0pupqdhpkk-di5gcr

https://wolfram.com/xid/0pupqdhpkk-bq2c6r
使用 Interval 和 CenteredInterval 对象计算最坏情况下的保证区间:
https://wolfram.com/xid/0pupqdhpkk-k9j849
https://wolfram.com/xid/0pupqdhpkk-dymc0w
https://wolfram.com/xid/0pupqdhpkk-lmyeh7
https://wolfram.com/xid/0pupqdhpkk-d918ed
或者使用 Around 计算平均情况统计区间:
https://wolfram.com/xid/0pupqdhpkk-cw18bq
https://wolfram.com/xid/0pupqdhpkk-2g
或使用 MatrixFunction 计算矩阵 SinDegrees 函数:
https://wolfram.com/xid/0pupqdhpkk-o5jpo
指定值 (6)
固定点的 SinDegrees 值:
https://wolfram.com/xid/0pupqdhpkk-nww7l
SinDegrees 在 30 度的有理倍数上有精确值:
https://wolfram.com/xid/0pupqdhpkk-cqeu9w
https://wolfram.com/xid/0pupqdhpkk-bdij6w
https://wolfram.com/xid/0pupqdhpkk-drqkdo
https://wolfram.com/xid/0pupqdhpkk-v87
更复杂的情况需要明确使用 FunctionExpand:
https://wolfram.com/xid/0pupqdhpkk-mnn
https://wolfram.com/xid/0pupqdhpkk-p3j
SinDegrees 的零点:
https://wolfram.com/xid/0pupqdhpkk-cw39qs
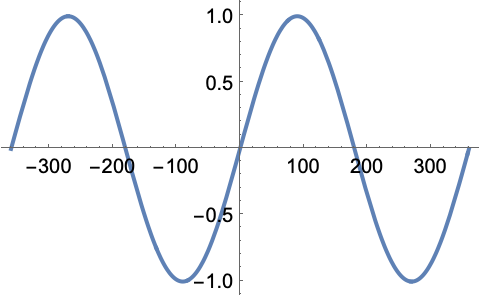
SinDegrees 的极值:
https://wolfram.com/xid/0pupqdhpkk-kb0ip3
https://wolfram.com/xid/0pupqdhpkk-0hynlo
https://wolfram.com/xid/0pupqdhpkk-f2hrld
https://wolfram.com/xid/0pupqdhpkk-cj5txq
可视化 (4)
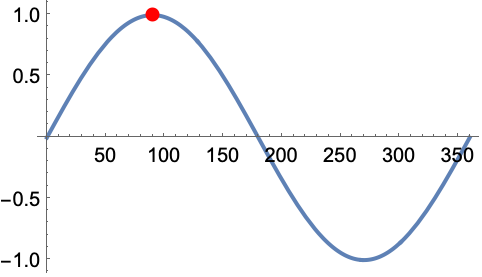
绘制 SinDegrees 函数:
https://wolfram.com/xid/0pupqdhpkk-ecj8m7
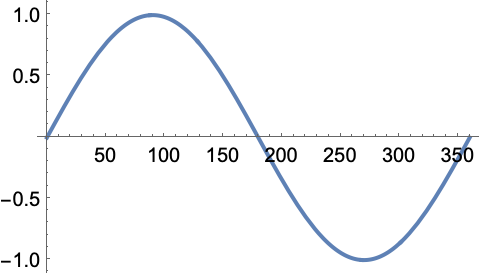
https://wolfram.com/xid/0pupqdhpkk-bomgjz
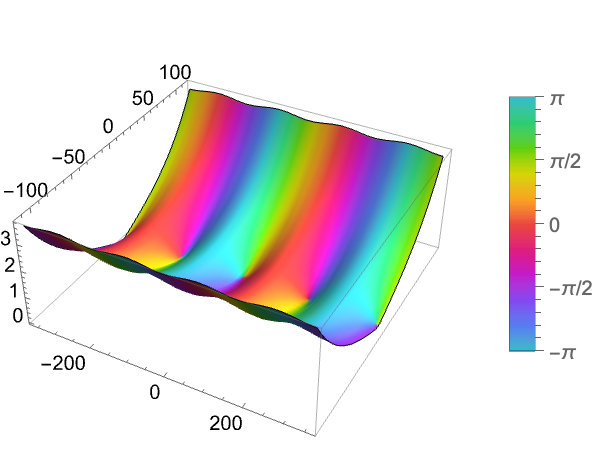
绘制 SinDegrees 的实部:
https://wolfram.com/xid/0pupqdhpkk-bo5grg
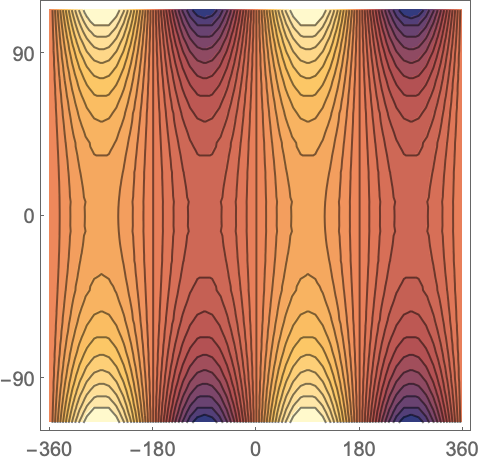
绘制 SinDegrees 的虚部:
https://wolfram.com/xid/0pupqdhpkk-q61pi
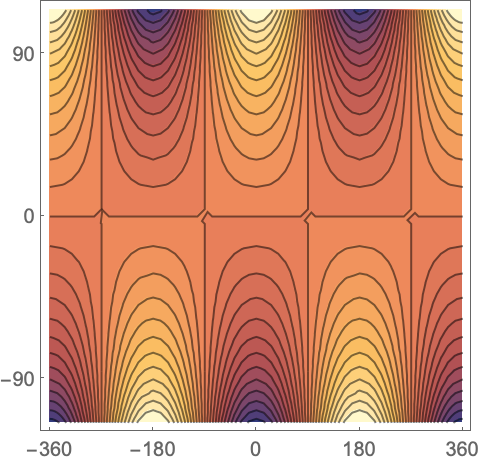
使用 SinDegrees 绘制极坐标图:
https://wolfram.com/xid/0pupqdhpkk-epb4bn
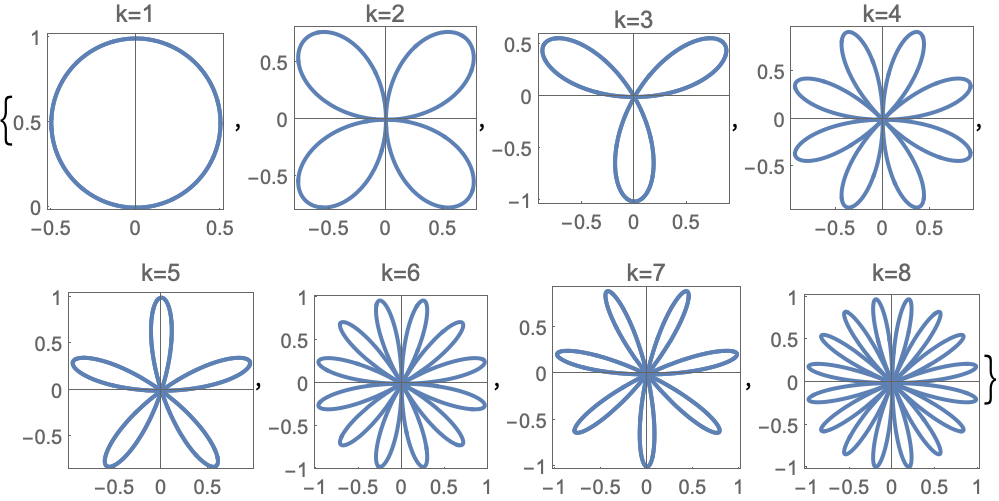
函数属性 (13)
SinDegrees 是一个周期为 360 度的周期函数:
https://wolfram.com/xid/0pupqdhpkk-zf82es
用 FunctionPeriod 检验:
https://wolfram.com/xid/0pupqdhpkk-ocqrm8
SinDegrees 对所有实值和复值有定义:
https://wolfram.com/xid/0pupqdhpkk-cl7ele
https://wolfram.com/xid/0pupqdhpkk-de3irc
SinDegrees 值域为 ![]() 和
和 ![]() 区间内的所有实值:
区间内的所有实值:
https://wolfram.com/xid/0pupqdhpkk-evf2yr
https://wolfram.com/xid/0pupqdhpkk-fphbrc
SinDegrees 是奇函数:
https://wolfram.com/xid/0pupqdhpkk-dnla5q
SinDegrees 具有镜像属性 ![]() :
:
https://wolfram.com/xid/0pupqdhpkk-heoddu
SinDegrees 是关于 x 的解析函数:
https://wolfram.com/xid/0pupqdhpkk-h5x4l2
SinDegrees 在特定范围内是单调函数:
https://wolfram.com/xid/0pupqdhpkk-g6kynf
https://wolfram.com/xid/0pupqdhpkk-nlz7s
SinDegrees 不是单射函数:
https://wolfram.com/xid/0pupqdhpkk-gi38d7
https://wolfram.com/xid/0pupqdhpkk-ctca0g
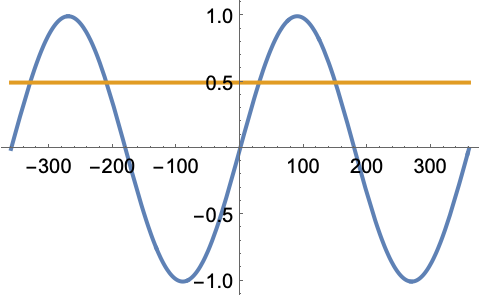
SinDegrees 不是满射函数:
https://wolfram.com/xid/0pupqdhpkk-hkqec4
https://wolfram.com/xid/0pupqdhpkk-hdm869
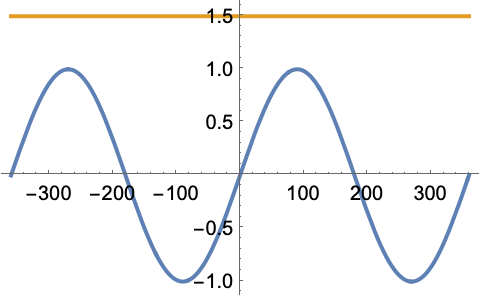
SinDegrees 既不是非负也不是非正:
https://wolfram.com/xid/0pupqdhpkk-84dui
SinDegrees 没有奇点或不连续点:
https://wolfram.com/xid/0pupqdhpkk-mdtl3h
https://wolfram.com/xid/0pupqdhpkk-mn5jws
SinDegrees 既不凸也不凹:
https://wolfram.com/xid/0pupqdhpkk-kdss3
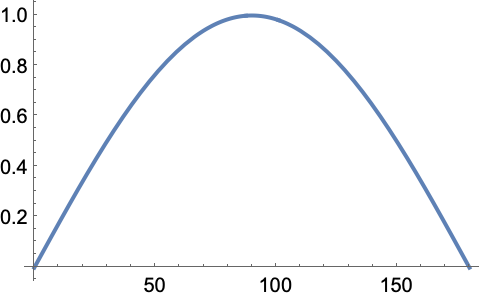
SinDegrees 对于区间 [0,180] 内的 x 为凹函数:
https://wolfram.com/xid/0pupqdhpkk-io426y
https://wolfram.com/xid/0pupqdhpkk-bb47uv
TraditionalForm 格式:
https://wolfram.com/xid/0pupqdhpkk-6k0d4
微分 (3)
https://wolfram.com/xid/0pupqdhpkk-mmas49
https://wolfram.com/xid/0pupqdhpkk-nfbe0l
https://wolfram.com/xid/0pupqdhpkk-56llx
积分 (3)
通过 Integrate 计算 SinDegrees 的不定积分:
https://wolfram.com/xid/0pupqdhpkk-bponid
一个周期内 SinDegrees 的定积分为 0:
https://wolfram.com/xid/0pupqdhpkk-b9jw7l
https://wolfram.com/xid/0pupqdhpkk-4nbst
https://wolfram.com/xid/0pupqdhpkk-c8i6nd

级数展开 (3)
使用 Series 求泰勒展开式:
https://wolfram.com/xid/0pupqdhpkk-ewr1h8
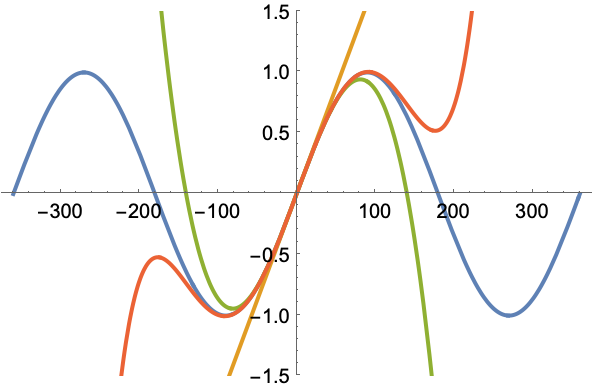
在 ![]() 周围绘制 SinDegrees 前三个近似:
周围绘制 SinDegrees 前三个近似:
https://wolfram.com/xid/0pupqdhpkk-binhar
https://wolfram.com/xid/0pupqdhpkk-f64drv
SinDegrees 可以应用于幂级数:
https://wolfram.com/xid/0pupqdhpkk-f7dy9o
函数恒等和化简 (5)
使用 TrigExpand 的双角公式:
https://wolfram.com/xid/0pupqdhpkk-mjplp7
https://wolfram.com/xid/0pupqdhpkk-nfe4y
https://wolfram.com/xid/0pupqdhpkk-kgd4gx
使用 TrigReduce 还原原始表达式:
https://wolfram.com/xid/0pupqdhpkk-ti7f8
使用 TrigFactor 将和转换为积:
https://wolfram.com/xid/0pupqdhpkk-j5kup
使用 TrigToExp 转换为指数:
https://wolfram.com/xid/0pupqdhpkk-u1m
函数表示 (4)
使用 CosDegrees 进行表示:
https://wolfram.com/xid/0pupqdhpkk-df304y
https://wolfram.com/xid/0pupqdhpkk-uopc8v
通过 CosDegrees、TanDegrees 和 CotDegrees 进行表示:
https://wolfram.com/xid/0pupqdhpkk-wdje4e
https://wolfram.com/xid/0pupqdhpkk-yo2yqd
通过 CscDegrees 进行表示:
https://wolfram.com/xid/0pupqdhpkk-3iqpk4
应用 (22)用该函数可以解决的问题范例
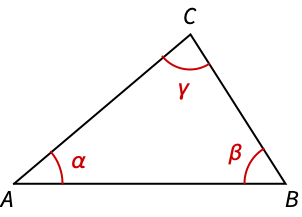
基本三角函数应用 (3)
已知 ![]() ,求角
,求角 ![]() 的 SinDegrees:
的 SinDegrees:
https://wolfram.com/xid/0pupqdhpkk-pzrtpu
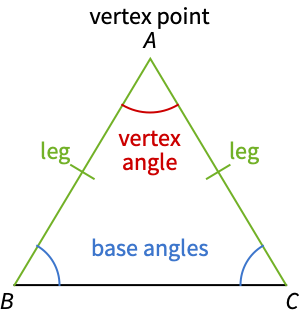
已知直角三角形斜边为 5,角度为 30 度,求该三角形缺失的对边长:
https://wolfram.com/xid/0pupqdhpkk-ull6kl
https://wolfram.com/xid/0pupqdhpkk-q0x
三角函数恒等式 (7)
使用和差公式计算 105 度的 SinDegrees 值:
https://wolfram.com/xid/0pupqdhpkk-uvn91a
https://wolfram.com/xid/0pupqdhpkk-22bxr8
https://wolfram.com/xid/0pupqdhpkk-lbx8rc
使用半角公式 ![]() 计算 15 度角的 SinDegrees 值:
计算 15 度角的 SinDegrees 值:
https://wolfram.com/xid/0pupqdhpkk-rj4ct4
将此结果与直接计算的 SinDegrees 进行比较:
https://wolfram.com/xid/0pupqdhpkk-w17g1e
使用三角乘积求和公式 ![]() 计算两个 SinDegrees 的乘积:
计算两个 SinDegrees 的乘积:
https://wolfram.com/xid/0pupqdhpkk-xthfig
将此结果与直接计算出的两个 SinDegrees 实例的乘积进行比较:
https://wolfram.com/xid/0pupqdhpkk-87co9l
https://wolfram.com/xid/0pupqdhpkk-zp5yby
https://wolfram.com/xid/0pupqdhpkk-ci2htt
https://wolfram.com/xid/0pupqdhpkk-fnpfz4
https://wolfram.com/xid/0pupqdhpkk-0gu9is
https://wolfram.com/xid/0pupqdhpkk-2rbc0y
https://wolfram.com/xid/0pupqdhpkk-g47lx
https://wolfram.com/xid/0pupqdhpkk-ivjwir
三角方程 (2)
https://wolfram.com/xid/0pupqdhpkk-9jfx4g
https://wolfram.com/xid/0pupqdhpkk-qmswx7

https://wolfram.com/xid/0pupqdhpkk-7wne7o
三角不等式 (2)
高级应用 (8)
https://wolfram.com/xid/0pupqdhpkk-hhm
https://wolfram.com/xid/0pupqdhpkk-v1r5y3
https://wolfram.com/xid/0pupqdhpkk-n96
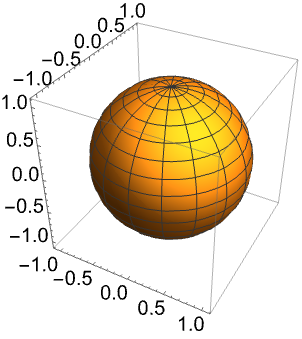

https://wolfram.com/xid/0pupqdhpkk-js6
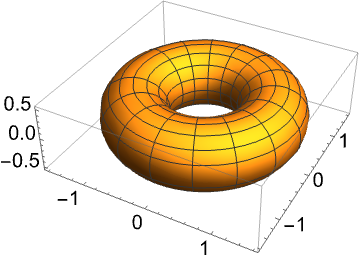
https://wolfram.com/xid/0pupqdhpkk-j8l
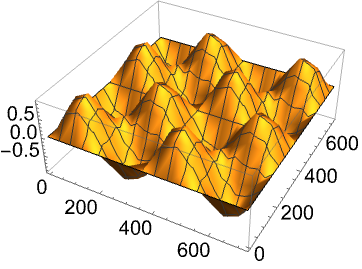
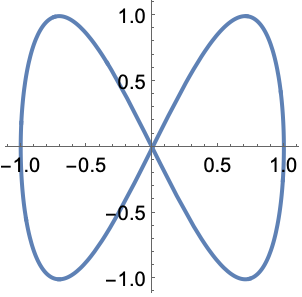
求几乎无处微分的 Riemann–Weierstrass 函数近似:
https://wolfram.com/xid/0pupqdhpkk-g5b9ii

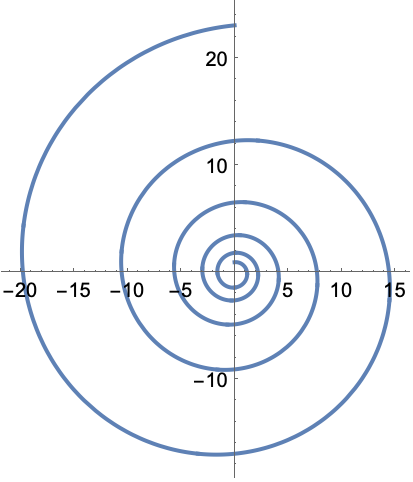
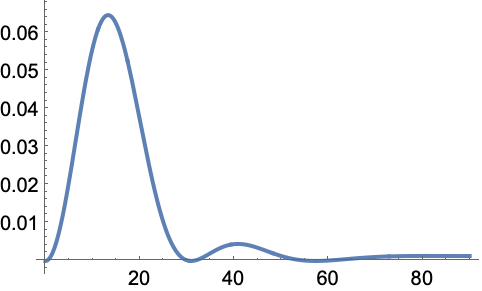
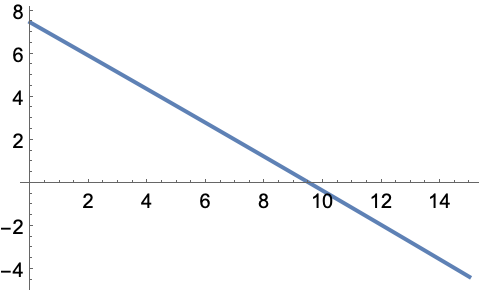
圆形孔径的 Fraunhofer 衍射图样强度与衍射角的关系:
https://wolfram.com/xid/0pupqdhpkk-dvkhak
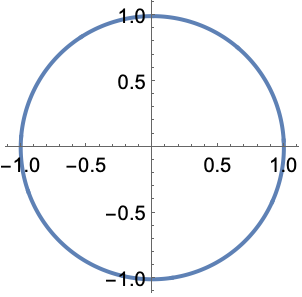
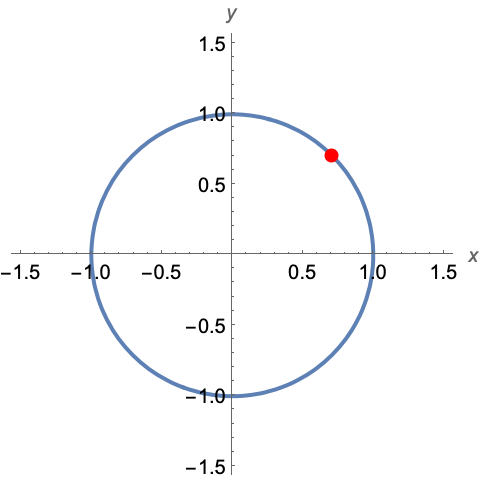
使用 CosDegrees 和 SinDegrees 函数求单位圆中的某一点:
https://wolfram.com/xid/0pupqdhpkk-u80xp
属性和关系 (11)函数的属性及与其他函数的关联
https://wolfram.com/xid/0pupqdhpkk-qtrjkp
https://wolfram.com/xid/0pupqdhpkk-mz1
https://wolfram.com/xid/0pupqdhpkk-ted
https://wolfram.com/xid/0pupqdhpkk-vc2
https://wolfram.com/xid/0pupqdhpkk-54
https://wolfram.com/xid/0pupqdhpkk-vtf
https://wolfram.com/xid/0pupqdhpkk-vt3
https://wolfram.com/xid/0pupqdhpkk-j62
https://wolfram.com/xid/0pupqdhpkk-wgk
使用 FunctionExpand 可用根式表示 SinDegrees:
https://wolfram.com/xid/0pupqdhpkk-sub
https://wolfram.com/xid/0pupqdhpkk-g37
https://wolfram.com/xid/0pupqdhpkk-qcr
https://wolfram.com/xid/0pupqdhpkk-n6i
https://wolfram.com/xid/0pupqdhpkk-ipj

https://wolfram.com/xid/0pupqdhpkk-fwo
https://wolfram.com/xid/0pupqdhpkk-ds23ya
SinDegrees 的零点:
https://wolfram.com/xid/0pupqdhpkk-kku
将 FunctionExpand 应用于 SinDegrees 会生成以弧度表示的三角函数表达式:
https://wolfram.com/xid/0pupqdhpkk-fujuf5
https://wolfram.com/xid/0pupqdhpkk-roe9wv
将 ExpToTrig 应用于 TrigToExp 的输出,将生成以弧度表示的三角函数:
https://wolfram.com/xid/0pupqdhpkk-bl9bv4
https://wolfram.com/xid/0pupqdhpkk-lc9q8e
https://wolfram.com/xid/0pupqdhpkk-egxn3i
SinDegrees 是一个数值函数:
https://wolfram.com/xid/0pupqdhpkk-qwm
可能存在的问题 (1)常见隐患和异常行为
巧妙范例 (5)奇妙或有趣的实例
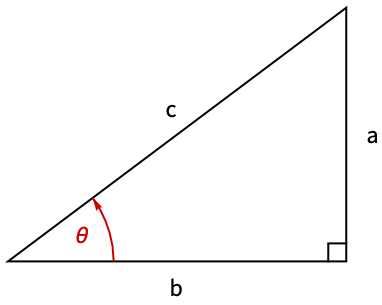

https://wolfram.com/xid/0pupqdhpkk-2yke9s
https://wolfram.com/xid/0pupqdhpkk-nytfuw
https://wolfram.com/xid/0pupqdhpkk-cvyldi
https://wolfram.com/xid/0pupqdhpkk-r4zle9
https://wolfram.com/xid/0pupqdhpkk-eag
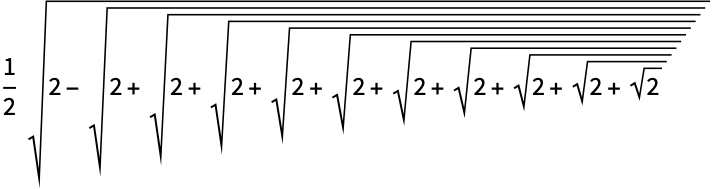
https://wolfram.com/xid/0pupqdhpkk-kk5
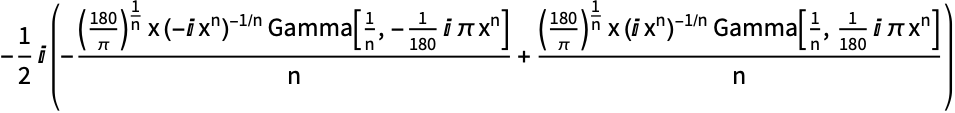
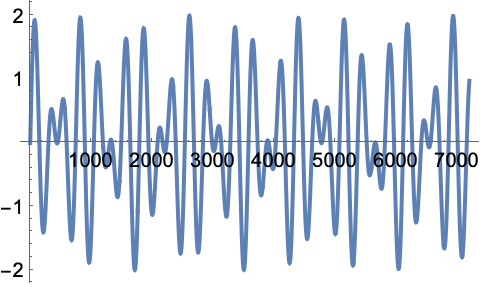
非一致性波(Non-commensurate waves,准周期函数):
https://wolfram.com/xid/0pupqdhpkk-snh
Wolfram Research (2024),SinDegrees,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SinDegrees.html.文本
Wolfram Research (2024),SinDegrees,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SinDegrees.html.
Wolfram Research (2024),SinDegrees,Wolfram 语言函数,https://reference.wolfram.com/language/ref/SinDegrees.html.CMS
Wolfram 语言. 2024. "SinDegrees." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SinDegrees.html.
Wolfram 语言. 2024. "SinDegrees." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/SinDegrees.html.APA
Wolfram 语言. (2024). SinDegrees. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SinDegrees.html 年
Wolfram 语言. (2024). SinDegrees. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/SinDegrees.html 年BibTeX
@misc{reference.wolfram_2025_sindegrees, author="Wolfram Research", title="{SinDegrees}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/SinDegrees.html}", note=[Accessed: 02-April-2025
]}BibLaTeX
@online{reference.wolfram_2025_sindegrees, organization={Wolfram Research}, title={SinDegrees}, year={2024}, url={https://reference.wolfram.com/language/ref/SinDegrees.html}, note=[Accessed: 02-April-2025
]}