StraussHardcorePointProcess

StraussHardcorePointProcess[μ,γ,rh,rs,d]

における，一定強度 μ，相互作用パラメータ γ，ハードコア相互作用半径 rh，Strauss相互作用半径 rsのStraussハードコア点過程を表す．

詳細

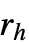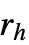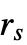  • StraussHardcorePointProcessは，点が互いにハードコア半径 r_(h)より近付くことができず，互いに半径 r_(h)から半径 r_(s)までの距離にある点には反発し合う対相互作用があり，その他は一様分布に従っている点配置をモデル化する．
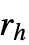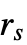  • Straussハードコアモデルは，一般に，r_(h)と r_(s)がそれぞれ木の幹と林冠の半径に対応する森林の木々のような点過程のモデル化に使われる．
  •     
  • Straussハードコア点過程は，その強度 μ と，どちらも γ，rh，rsによって以下のようにパラメータ化される対ポテンシャル 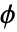あるいは対相互作用 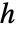によってGibbsPointProcessとして定義される．
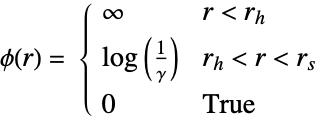
  • 対ポテンシャル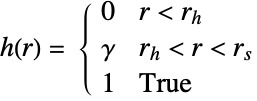
    対相互作用
  • 観測領域 reg におけるStraussハードコア点過程からの点配置 は，PoissonPointProcess[1,d]について，mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])に比例する密度関数 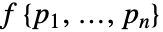を持つ．
  • 点 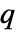を点配置に加える際のPapangelou条件密度 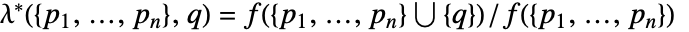は mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm])である．
  • StraussHardcorePointProcessでは，μ，γ，rh，rs は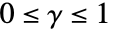となるような正の数でよく，d は任意の正の整数でよい．
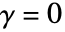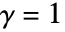  • ，あるいは 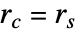のとき，StraussHardcorePointProcessは簡約されてHardcorePointProcessになる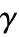．gamma の値が小さいと点は 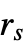r_(s)より近付けない．
  • 次は，StraussPointProcessにおけるRandomPointConfiguration中の可能なMethod設定である．
  • "MCMC"マルコフ(Markov)鎖モンテカルロ法による出生死滅過程
    "Exact"過去からのカップリング法
  • 次は，EstimatedPointProcess内のStraussHardcorePointProcessについてのPointProcessEstimatorの可能な設定である．
  • Automaticパラメータ推定器を自動選択する
    "MaximumPseudoLikelihood"擬似尤度を最大にする
  • StraussHardcorePointProcessは，RipleyKやRandomPointConfiguration等の関数と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (2)

Straussハードコア点過程からサンプルを取る：

サンプル内の点を可視化する：

地理領域からサンプルを取る：

点を可視化する：

スコープ  (5)

Straussハードコア点過程から3つの実現を生成する：

パラメータを推定する：

地理領域内のStraussハードコア点過程から3つの実現を生成する：

点配置を可視化する：

パラメータを推定する：

ハードコア半径を増しながらサンプルを生成する：

Strauss半径を増しながらサンプルを生成する：

相互作用パラメータ γ を増しながらサンプルを生成する：

オプション  (4)

Method  (4)

マルコフ鎖モンテカルロ法を使ってシミュレーションを行う：

サンプラーへの再帰呼出しの回数を指定する：

実行長を指定する：

シミュレーションの初期状態を与える：

シミュレーションの初期状態を与える：

結果が以下のようになるためには，初期状態が非零密度でなければならない：

点と点の間の最短距離がハードコア半径よりも短いかどうかをチェックする：

厳密法を使ったサンプル：

サンプル中の点を可視化する：

考えられる問題  (1)

デフォルトで，点の数が定常状態に収束するまで，あるいは反復のデフォルト数に達するまで，シミュレーションが続けられる：

サンプラーへの再帰呼出しの数を増やす：

実行長を大きくする：

Wolfram Research (2020), StraussHardcorePointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html.

テキスト

Wolfram Research (2020), StraussHardcorePointProcess, Wolfram言語関数， https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html.

CMS

Wolfram Language. 2020. "StraussHardcorePointProcess." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html.

APA

Wolfram Language. (2020). StraussHardcorePointProcess. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html

BibTeX

@misc{reference.wolfram_2024_strausshardcorepointprocess, author="Wolfram Research", title="{StraussHardcorePointProcess}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_strausshardcorepointprocess, organization={Wolfram Research}, title={StraussHardcorePointProcess}, year={2020}, url={https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html}, note=[Accessed: 18-November-2024 ]}