StraussHardcorePointProcess
StraussHardcorePointProcess[μ,γ,rh,rs,d]
表示 ![]() 中的一个 Strauss 硬核点过程,其恒定强度为 μ,交互参数为 γ,硬核交互半径为 rh,Strauss 交互半径为 rs.
中的一个 Strauss 硬核点过程,其恒定强度为 μ,交互参数为 γ,硬核交互半径为 rh,Strauss 交互半径为 rs.
更多信息


- StraussHardcorePointProcess 模拟点布局,其中点不能在相互硬核半径
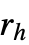 的范围内,对于在相互半径
的范围内,对于在相互半径 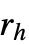 和
和 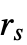 之间的点会有一个恒定配对互斥作用,否则均匀分布.
之间的点会有一个恒定配对互斥作用,否则均匀分布. - Strauss 硬核模型通常用于模拟比如森林里的树木这样的点过程,其中
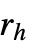 和
和 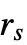 分别对应树干和冠层的半径.
分别对应树干和冠层的半径. -

- Strauss 硬核点过程可被定义为关于其强度 μ 和其配对势能
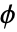 或配对作用
或配对作用 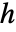 的 GibbsPointProcess,节课通过 γ,rh 和 rs 按照下列方式参数化:
的 GibbsPointProcess,节课通过 γ,rh 和 rs 按照下列方式参数化: -
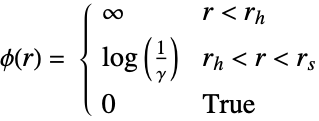
配对势能 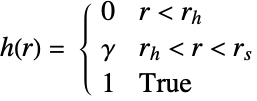
配对作用 - 在观察区域 reg 中,Strauss 硬核点过程的点布局
 有关于 PoissonPointProcess[1,d] 的与
有关于 PoissonPointProcess[1,d] 的与 ![mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm]) mu^n product_(i!=j)h(TemplateBox[{{{p, _, i}, -, {p, _, j}}}, Norm])](Files/StraussHardcorePointProcess.zh/13.png) 成比例的密度函数
成比例的密度函数 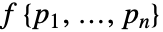 .
. - 将点
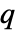 加入布局
加入布局  的 Papangelou 条件密度
的 Papangelou 条件密度 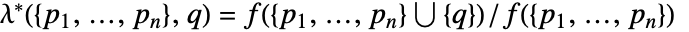 为
为 ![mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm]) mu product_ih(TemplateBox[{{{p, _, i}, -, q}}, Norm])](Files/StraussHardcorePointProcess.zh/18.png) .
. - StraussHardcorePointProcess 允许 μ,γ,rh 和 rs t为正数使得
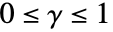 ,且 d 为任意正整数.
,且 d 为任意正整数. - 当
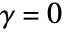 ,
,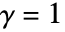 或
或 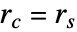 时,StraussHardcorePointProcess 化简为 HardcorePointProcess.
时,StraussHardcorePointProcess 化简为 HardcorePointProcess. 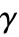 的值越小,会抑制距离小于
的值越小,会抑制距离小于 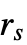 的点.
的点. - RandomPointConfiguration 中 StraussPointProcess 的可能 Method 设定为:
-
"MCMC" 马尔科夫链蒙特卡洛方法初始和消亡 "Exact" 从过去耦合 - EstimatedPointProcess 中 StraussHardcorePointProcess 的可能 PointProcessEstimator 设定为:
-
Automatic 自动选择参数估计量 "MaximumPseudoLikelihood" 最大化伪似然度 - StraussHardcorePointProcess 可与诸如 RipleyK 和 RandomPointConfiguration 这样的函数一起使用.
范例
打开所有单元关闭所有单元范围 (5)
选项 (4)
Wolfram Research (2020),StraussHardcorePointProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html.
文本
Wolfram Research (2020),StraussHardcorePointProcess,Wolfram 语言函数,https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html.
CMS
Wolfram 语言. 2020. "StraussHardcorePointProcess." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html.
APA
Wolfram 语言. (2020). StraussHardcorePointProcess. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/StraussHardcorePointProcess.html 年