TargetStructure
線形代数関数のオプションで,関数の結果の表示方法を指定する.
詳細



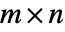 行列は,格納効率と行列への適用効率がよい
行列は,格納効率と行列への適用効率がよい 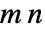 よりも少ない要素で表せることがある.TargetStructureを使うと,可能な場合は常に関数が行列結果を構造化表現で返すようになる.
よりも少ない要素で表せることがある.TargetStructureを使うと,可能な場合は常に関数が行列結果を構造化表現で返すようになる.- 御湯列を構築する関数におけるTargetStructureの可能な設定には以下がある.
-
Automatic 返す表現を自動的に選択する "Dense" 行列を密な配列として表す "Sparse" 行列を疎な配列として表す "Structured" 行列を構造化配列として表す - 次は,TargetStructureオプションを持つ行列のコンストラクタ関数と対応するサポートされる設定である.
-
BlockDiagonalMatrix "Dense", "Structured", "Sparse" BlockLowerTriangularMatrix "Dense", "Structured", "Sparse" BlockUpperTriangularMatrix "Dense", "Structured", "Sparse" CauchyMatrix "Dense", "Structured" DiagonalMatrix "Dense", "Structured", "Sparse" FourierMatrix "Dense", "Structured" HankelMatrix "Dense", "Structured" HilbertMatrix "Dense", "Cauchy", "Hankel" IdentityMatrix "Dense", "Structured", "Sparse" LowerTriangularMatrix "Dense", "Structured", "Sparse" PermutationMatrix "Dense", "Structured", "Sparse" ToeplitzMatrix "Dense", "Structured" UpperTriangularMatrix "Dense", "Structured", "Sparse" VandermondeMatrix "Dense", "Structured" - 関数のIdentityMatrix,DiagonalMatrix,ToeplitzMatrix,HankelMatrix,FourierMatrixの設定をTargetStructureAutomaticにすると,現行の閾値以下では密な結果を,それ以外の場合は構造化配列を返す.
- それ以外のすべての行列コンストラクタ関数については,TargetStructureAutomaticと設定すると構造化配列の結果が返される.
- 行列分解関数におけるTargetStructureの可能な設定には以下がある.
-
Automatic 返す表現を自動選択する "Dense" すべての行列を密な配列として表す "Structured" 可能な場合は常にすべての行列を構造化配列として表す - 次は,TargetStructureオプションを持つ行列分解関数と対応するサポートされる設定である.
-
CholeskyDecomposition "Dense", "Structured" CoreNilpotentDecomposition "Dense", "Structured" - 関数LowerTriangularizeおよびUpperTriangularizeはTargetStructureオプションもサポートする.次は,可能な設定である.
-
Automatic 入力行列のタイプを保持する "Dense" 行列を密な配列として表す "Sparse" 行列を疎な配列として表す "Structured" 行列を構造化配列として表す - TargetStructure"Structured"と設定すると,適応する場合は常に,LowerTriangularizeはLowerTriangularMatrixの結果を返し,UpperTriangularizeはUpperTriangularMatrixの結果を返す.
- TargetStructureNoneの設定はTargetStructure"Dense"に等しい.
例題
すべて開くすべて閉じる例 (3)
スコープ (8)
行列のコンストラクタ (4)
行列分解 (2)
コレスキー(Cholesky)三角形をUpperTriangularMatrixとして表す:
TargetStructure"Structured"とすると,コア部分とベキ零部分がBlockDiagonalMatrixにまとめられる:
その他の関数 (2)
TargetStructure"Dense"のとき,関数UpperTriangularizeは密な行列を返す:
TargetStructure"Sparse"のときは疎な行列が返される:
TargetStructure"Structured"のときは構造化配列が返される:
TargetStructureAutomaticと設定すると,入力が密な行列なら関数LowerTriangularizeは密な行列を与える:
アプリケーション (3)
テキスト
Wolfram Research (2023), TargetStructure, Wolfram言語関数, https://reference.wolfram.com/language/ref/TargetStructure.html.
CMS
Wolfram Language. 2023. "TargetStructure." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/TargetStructure.html.
APA
Wolfram Language. (2023). TargetStructure. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/TargetStructure.html