TargetStructure
是线性代数函数的一个选项,指定如何表示函数产生的结果.
更多信息



- 有时,可以用少于
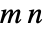 个元素表示
个元素表示 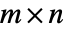 矩阵,这样可以使矩阵的存储变得更高效,还可以提高矩阵运算的效率. 可能的情况下,TargetStructure 允许函数以结构化表示的形式返回结果.
矩阵,这样可以使矩阵的存储变得更高效,还可以提高矩阵运算的效率. 可能的情况下,TargetStructure 允许函数以结构化表示的形式返回结果. - 用于构建矩阵的函数中 TargetStructure 的可能设置包括:
-
Automatic 自动选择如何表示返回的结果 "Dense" 用稠密数组表示矩阵 "Sparse" 用稀疏数组表示矩阵 "Structured" 用结构化数组表示矩阵 - 具有 TargetStructure 选项的矩阵构造函数及相应的设置如下:
-
BlockDiagonalMatrix "Dense", "Structured", "Sparse" BlockLowerTriangularMatrix "Dense", "Structured", "Sparse" BlockUpperTriangularMatrix "Dense", "Structured", "Sparse" CauchyMatrix "Dense", "Structured" DiagonalMatrix "Dense", "Structured", "Sparse" FourierMatrix "Dense", "Structured" HankelMatrix "Dense", "Structured" HilbertMatrix "Dense", "Cauchy", "Hankel" IdentityMatrix "Dense", "Structured", "Sparse" LowerTriangularMatrix "Dense", "Structured", "Sparse" PermutationMatrix "Dense", "Structured", "Sparse" ToeplitzMatrix "Dense", "Structured" UpperTriangularMatrix "Dense", "Structured", "Sparse" VandermondeMatrix "Dense", "Structured" - 对于函数 IdentityMatrix、DiagonalMatrix、ToeplitzMatrix、HankelMatrix 和 FourierMatrix,设置 TargetStructureAutomatic 对应于函数返回低于预设阈值的密集结果,否则返回结构化数组.
- 对于所有其他矩阵构造函数,设置 TargetStructureAutomatic 对应于返回结构化数组结果.
- 矩阵分解函数中 TargetStructure 的可能设置包括:
-
Automatic 自动选择如何表示返回的结果 "Dense" 用稠密数组表示所有矩阵 "Structured" 尽可能地将所有矩阵表示为结构化数组 - 具有 TargetStructure 选项的矩阵分解函数及相应的设置如下:
-
CholeskyDecomposition "Dense", "Structured" CoreNilpotentDecomposition "Dense", "Structured" - 函数 LowerTriangularize 和 UpperTriangularize 也支持 TargetStructure 选项. 可能的设置包括:
-
Automatic 保留输入矩阵的类型 "Dense" 用稠密数组表示矩阵 "Sparse" 用稀疏数组表示矩阵 "Structured" 用结构化数组表示矩阵 - 当设置为 TargetStructure"Structured" 时,可能的情况下,LowerTriangularize 返回的结果为 LowerTriangularMatrix,而 UpperTriangularize 返回的结果是 UpperTriangularMatrix.
- 设置 TargetStructureNone 等价于 TargetStructure"Dense".
范例
打开所有单元关闭所有单元基本范例 (3)
范围 (8)
矩阵构造函数 (4)
矩阵分解 (2)
用 UpperTriangularMatrix 表示 Cholesky 三角:
当设置 TargetStructure"Structured" 时,核心部分和幂零部分被放在一个 BlockDiagonalMatrix 中:
其他函数 (2)
当设置 TargetStructure"Dense" 时,函数 UpperTriangularize 返回一个稠密矩阵:
当设置 TargetStructure"Sparse" 时,返回稀疏数组:
当设置 TargetStructure"Structured"时,返回结构化数组:
当设置 TargetStructureAutomatic 时,如果输入是稠密矩阵,函数 LowerTriangularize 给出稠密矩阵:
应用 (3)
Wolfram Research (2023),TargetStructure,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TargetStructure.html.
文本
Wolfram Research (2023),TargetStructure,Wolfram 语言函数,https://reference.wolfram.com/language/ref/TargetStructure.html.
CMS
Wolfram 语言. 2023. "TargetStructure." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/TargetStructure.html.
APA
Wolfram 语言. (2023). TargetStructure. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/TargetStructure.html 年