Variance
詳細




- Varianceは,データあるいは分布の分散を測定する.
- Variance[data]は不偏分散推定を与える.
- VectorQ data
 についての分散推定
についての分散推定 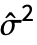 は,実数については
は,実数については 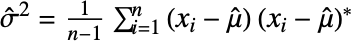 で,虚数については
で,虚数については 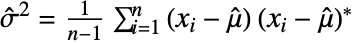 で与えられる.
で与えられる.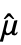 =Mean[data]である.
=Mean[data]である. - MatrixQ data についての分散推定
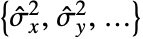 は各列ベクトルについて計算される.iVariance[{{x1,y1,…},{x2,y2,…},…}]は{Variance[{x1,x2,…}],Variance[{y1,y2,…}]}に等しい. »
は各列ベクトルについて計算される.iVariance[{{x1,y1,…},{x2,y2,…},…}]は{Variance[{x1,x2,…}],Variance[{y1,y2,…}]}に等しい. » - ArrayQ data の分散はArrayReduce[Variance,data,1]に等しい. »
- 重み付き実数WeightedData[{x1,x2,…},{w1,w2,…}]の分散は
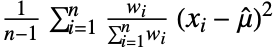 で与えられる. »
で与えられる. » - Varianceは,数値と記号両方の data を扱う.
- data は次の追加的な形式と解釈を持つことがある.
-
Association 値(キーは無視される) » SparseArray 配列として,Normal[data]に等しい » QuantityArray 配列としての数量 » WeightedData 重み付きの分散,もとになっているEmpiricalDistributionに基づく » EventData もとになっているSurvivalDistributionに基づく » TimeSeries, TemporalData, … ベクトルまたは値の配列(タイムスタンプは無視される) » Image,Image3D RGBチャンネル値またはグレースケール強度値 » Audio 全チャンネルの振幅値 » DateObject, TimeObject 日付のリストまたは時間のリスト » - 一変量分布 dist の分散は σ2=Expectation[(x-μ)2,xdist]で与えられる.ただし,μ=Mean[dist]である. »
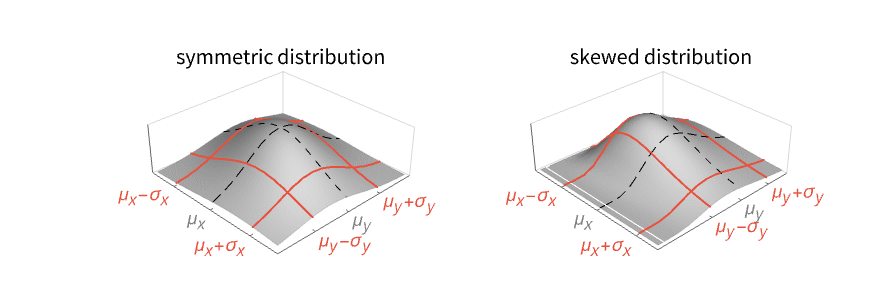
- 多変量分布 dist の分散は{σx2,σy2,…}=Expectation[{(x-μx)2,(y-μy)2,…},{x,y,…}dist]で与えられる. »
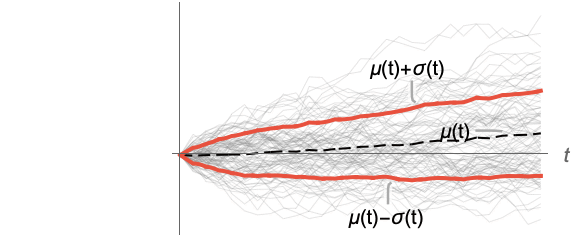
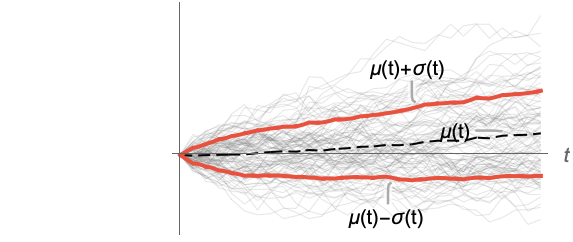
- ランダム過程 proc については,分散関数は時点 t におけるスライス分布SliceDistribution[proc,t]について σ[t]2=Variance[SliceDistribution[proc,t]]として計算できる. »
例題
すべて開く すべて閉じるスコープ (22)
基本的な用法 (7)
配列データ (5)
行列についてのVarianceは列ごとの分散を与える:
テンソルについてのVarianceは第1レベルの列ごとの分散を与える:
Varianceは,入力がAssociationのときはその値に作用する:
SparseArrayデータは密な配列と同じように使うことができる:
QuantityArrayの分散を求める:
画像データと音声データ (2)
アプリケーション (5)
Varianceは分散度である:
移動分散で平滑化することで,データのボラティリティを比較する:
1860年から1959年までの年ごとの優れた発明や科学的発見の平均と分散を求める:
特性と関係 (11)
Varianceの平方根はStandardDeviationである:
Varianceは,Meanからの偏差の平方したNormをスケールしたものである:
VarianceはスケールしたCentralMomentである:
Varianceの平方根は,偏差のスケールしたRootMeanSquareである:
VarianceはMeanからの偏差を平方したものをスケールしたMeanである:
MeanからのスケールしたSquaredEuclideanDistanceとしてのVariance:
すべての絶対偏差が1より小さい場合,VarianceはMeanDeviationより小さい:
すべての絶対偏差が1より大きい場合,VarianceはMeanDeviationより大きい:
Expectationとしてのランダム変数のVariance:
Varianceは,偏りのないサンプル推定を与える:
偏りがないとは,母分布についてのサンプル分散の期待値がもとになっている分布の分散と等しいことを意味する:
Varianceは偏りのない重み付きのサンプル推定を与える:
おもしろい例題 (1)
20個,100個,300個のサンプルについてのVariance推定値の分布:
関連項目
StandardDeviation Covariance Correlation TrimmedVariance WinsorizedVariance BiweightMidvariance QnDispersion SnDispersion Mean MeanDeviation MedianDeviation Kurtosis CentralMoment Expectation
Function Repository: PopulationVariance VarianceAround VarianceRatioCI PooledVariance GeneralizedVariance HedgesG
関連するガイド
-
▪
- 記述統計 ▪
- 統計的データ解析 ▪
- GPU計算 ▪
- リストへの数学的およびカウント操作 ▪
- 時系列の処理 ▪
- 統計モーメントと母関数 ▪
- 数値データ ▪
- 科学的データ解析 ▪
- 中学・高校における教育 ▪
- 画像の処理と解析 ▪
- 有限数学 ▪
- 確率・統計 ▪
- Appleを使ったGPU計算 ▪
- NVIDIAを使ったGPU計算 ▪
- 日付と時刻 ▪
- 信号の可視化と解析 ▪
- 音声処理 ▪
- 記号的なベクトル,行列,配列
履歴
2003 で導入 (5.0) | 2007 で更新 (6.0) ▪ 2023 (13.3) ▪ 2024 (14.1)
テキスト
Wolfram Research (2003), Variance, Wolfram言語関数, https://reference.wolfram.com/language/ref/Variance.html (2024年に更新).
CMS
Wolfram Language. 2003. "Variance." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Variance.html.
APA
Wolfram Language. (2003). Variance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Variance.html
BibTeX
@misc{reference.wolfram_2025_variance, author="Wolfram Research", title="{Variance}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Variance.html}", note=[Accessed: 02-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_variance, organization={Wolfram Research}, title={Variance}, year={2024}, url={https://reference.wolfram.com/language/ref/Variance.html}, note=[Accessed: 02-March-2026]}

