WaringYuleDistribution
形状母数が α のユール(Yule)分布を表す.
形状母数が α と β のウェアリング(Waring)分布を表す.
詳細
- WaringYuleDistribution[α]はYule–Simon分布としても知られている.
- ウェアリング・ユール分布における整数値
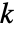 の確率は以下に比例する.
の確率は以下に比例する. -
WaringYuleDistribution[α] ![(TemplateBox[{{k, +, 1}}, Gamma])/(TemplateBox[{{k, +, alpha, +, 2}}, Gamma]) (TemplateBox[{{k, +, 1}}, Gamma])/(TemplateBox[{{k, +, alpha, +, 2}}, Gamma])](Files/WaringYuleDistribution.ja/2.png)
WaringYuleDistribution[α,β] ![(TemplateBox[{{k, +, beta}}, Gamma])/(TemplateBox[{{k, +, alpha, +, beta, +, 1}}, Gamma]) (TemplateBox[{{k, +, beta}}, Gamma])/(TemplateBox[{{k, +, alpha, +, beta, +, 1}}, Gamma])](Files/WaringYuleDistribution.ja/3.png)
- WaringYuleDistributionでは,α と β は任意の正の実数でよい.
- WaringYuleDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- WaringYuleDistribution[α,β]は,
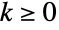 の整数値について定義され,正の実数母数 α および β(「形状母数」と呼ばれる)について定義される離散統計分布を表す.ウェアリング・ユール分布は,離散的で単調減少であり,全体的な形(広がりと傾斜の度合い)が α と β の値によって決定される確率密度関数(PDF)を持つ.ウェアリング・ユール分布はウェアリング分布と呼ばれることがあるのに対し,WaringYuleDistribution[α,1]に等しい引数が1つの形のWaringYuleDistribution[α]はユール分布あるいはユール・サイモン分布と呼ばれることが多い.
の整数値について定義され,正の実数母数 α および β(「形状母数」と呼ばれる)について定義される離散統計分布を表す.ウェアリング・ユール分布は,離散的で単調減少であり,全体的な形(広がりと傾斜の度合い)が α と β の値によって決定される確率密度関数(PDF)を持つ.ウェアリング・ユール分布はウェアリング分布と呼ばれることがあるのに対し,WaringYuleDistribution[α,1]に等しい引数が1つの形のWaringYuleDistribution[α]はユール分布あるいはユール・サイモン分布と呼ばれることが多い. - ウェアリングの研究は18世紀まで遡ることができるが,ウェアリング・ユール分布の歴史は,基本的に,一引数形のユール・サイモン分布の生成に始まる.ユール・サイモン分布は,1950年代中頃,H. A. サイモンがはじめて包括的に研究し,サイモンによってイギリス人の統計学者であるG. U. ユールに因んで命名された.これはユールが1925年にこの分布を発見し,行動進化に関連した確率過程に適用したためである.上述した二引数形の一般化は1960年代のはじめのIrwinの研究まで遡ることができる.それから10年間でウェアリング・ユール分布の多くの一般化が発見され,研究された.そのような一般化が,ネットワーク分析,薬理科学,事故理論等と関連した現象の説明に使われた.
- RandomVariateを使って,ウェアリング・ユール分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,WaringYuleDistribution[α,β]](より簡略な表記では xWaringYuleDistribution[α,β])を使って,確率変数 x がウェアリング・ユール分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[WaringYuleDistribution[α,β],x]およびCDF[WaringYuleDistribution[α,β],x]を使って得られる.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.これらの数量はDiscretePlotを使って可視化することができる.
- DistributionFitTestを使って,与えられたデータ集合がウェアリング・ユール分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックウェアリング・ユール分布を推定することが,FindDistributionParametersを使ってデータをウェアリング・ユール分布にフィットすることができる.ProbabilityPlotを使って記号ウェアリング・ユール分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ウェアリング・ユール分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたウェアリング・ユール分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってウェアリング・ユール分布を含む高次元分布を構築することが,ProductDistributionを使ってウェアリング・ユール分布を含む独立成分分布の結合分布を計算することができる.
- WaringYuleDistributionは他の数多くの統計分布と関連している.この分布は,WaringYuleDistribution[α,β]の確率密度関数がBetaNegativeBinomialDistribution[α,β,1]のそれと厳密に等しいという意味で,BetaNegativeBinomialDistributionの特殊ケースである.さらに,WaringYuleDistributionは,WaringYuleDistribution[a]の確率密度関数が
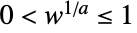 のときは wUniformDistribution[]についてGeometricDistribution[w1/a]のそれと厳密に等しいという意味で,GeometricDistributionとUniformDistributionの母数混合分布(ParameterMixtureDistribution)として実現することができる.WaringYuleDistributionはPoissonDistribution,PoissonConsulDistribution,PolyaAeppliDistributionとも密接な関係がある.
のときは wUniformDistribution[]についてGeometricDistribution[w1/a]のそれと厳密に等しいという意味で,GeometricDistributionとUniformDistributionの母数混合分布(ParameterMixtureDistribution)として実現することができる.WaringYuleDistributionはPoissonDistribution,PoissonConsulDistribution,PolyaAeppliDistributionとも密接な関係がある.
例題
すべて開くすべて閉じるスコープ (7)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
ユール分布のMoment:
ユール分布のCentralMoment:
ユール分布のFactorialMoment:
ユール分布のCumulant:
ウェアリング分布のMoment:
ウェアリング分布のCentralMoment:
ウェアリング分布のFactorialMoment:
ウェアリング分布のCumulant:
アプリケーション (3)
WaringYuleDistributionの累積分布関数は右連続関数の例である:
属内で新たな種が発生する速度は ![]() である.一方,新たな属の発生はよりゆっくりした速度
である.一方,新たな属の発生はよりゆっくりした速度 ![]() で起る.すべての年齢の属サイズの制限周波数分布はWaringYuleDistributionで与えられる,
で起る.すべての年齢の属サイズの制限周波数分布はWaringYuleDistributionで与えられる,![]() を仮定する:
を仮定する:
文字と空白をランダムに選んで単語の集合を生成する.結果の単語の大きさはWaringYuleDistributionを使ってモデル化できる:
特性と関係 (5)
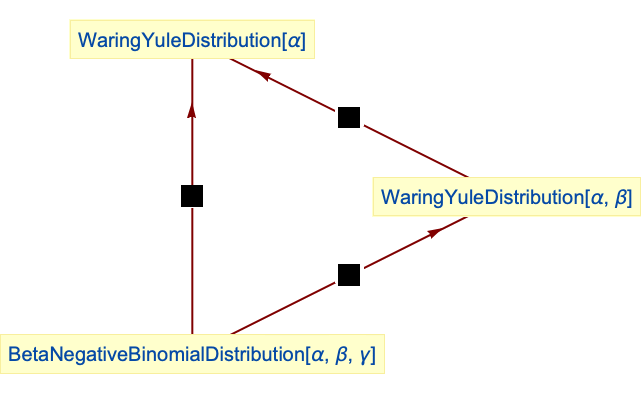
ユール分布はBetaNegativeBinomialDistributionの特殊ケースである:
ウェアリング分布はBetaNegativeBinomialDistributionの特殊ケースである:
ウェアリング分布を β=1について簡約するとユール分布になる:
ユール分布はGeometricDistributionとUniformDistributionの母数混合として得られる:
テキスト
Wolfram Research (2010), WaringYuleDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/WaringYuleDistribution.html.
CMS
Wolfram Language. 2010. "WaringYuleDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaringYuleDistribution.html.
APA
Wolfram Language. (2010). WaringYuleDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaringYuleDistribution.html