WolframのWebサイトのコンテンツとインタラクトしたりフォームを送信したりするためには，JavaScriptを有効にしてください．有効にする方法

WaveletPhi

WaveletPhi[wave,x]

x で評価された記号ウェーブレット wave のスケーリング関数を与える．

WaveletPhi[wave]

スケーリング関数を純関数として与える．

詳細とオプション

スケーリング関数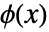は再帰方程式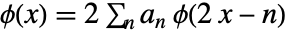を満足する．ただし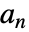，はローパスフィルタ係数である．
WaveletPhi[wave,x,"Dual"]はBiorthogonalSplineWaveletやReverseBiorthogonalSplineWavelet等の双直交ウェーブレットの双対スケーリング関数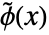を与える．
双対スケーリング関数は再帰方程式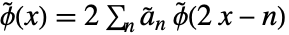を満足する．ただし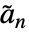，は双対ローパスフィルタ係数である．
使用可能なオプション
MaxRecursion 8 使用する再帰反復の数

WorkingPrecision MachinePrecision 内部計算で使用する精度

例題

すべて開くすべて閉じる

例 (2)

Haarスケーリング関数：

Symletスケーリング関数：

スコープ (4)

主スケーリング関数を計算する：

双対スケーリング関数：

HaarWaveletのスケーリング関数：

DaubechiesWavelet：

SymletWavelet：

CoifletWavelet：

BiorthogonalSplineWavelet：

ReverseBiorthogonalSplineWavelet：

ShannonWavelet：

BattleLemarieWavelet：

MeyerWavelet：

多変量のスケーリング関数およびウェーブレット関数はそれぞれ単変量関数の積である：

オプション (3)

MaxRecursion (1)

さまざまな再帰レベルでスケーリング関数をプロットする：

WorkingPrecision (2)

デフォルトで，WorkingPrecision->MachinePrecisionが使われる：

より精度の高いフィルタ計算を使う：

特性と関係 (4)

スケーリング関数を積分すると単位元になる．：

とりわけ：

は再帰方程式を満足する：

構成要素と再帰の総和をプロットする：

に対する周波数応答はで与えられる：

フィルタはローパスフィルタである：

のフーリエ(Fourier)変換はで与えられる：

おもしろい例題 (1)

スケーリング関数の平行移動と膨張をプロットする：

トップへ