Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

WaveletPsi

WaveletPsi[wave,x]

给出在 x 处的符号小波 wave 的小波函数 .

WaveletPsi[wave]

给出一个纯小波函数.

更多信息和选项

小波函数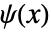满足递归方程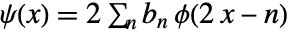，其中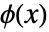是尺度函数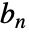，是高通滤波器的系数.
一个离散小波变换有效地以缩放的和平移的小波函数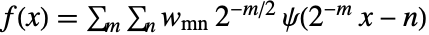形式表示信号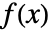，其中 .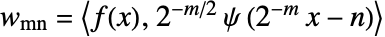
WaveletPsi[wave,x,"Dual"] 对于诸如 BiorthogonalSplineWavelet 和 ReverseBiorthogonalSplineWavelet 的双正交小波给出对偶小波函数 .
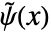对偶小波函数满足递归方程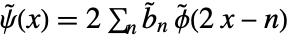，其中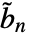是对偶高通滤波器的系数.
可使用以下选项：
MaxRecursion 8 递归迭代的次数

WorkingPrecision MachinePrecision 内部计算使用的精确度

范例

打开所有单元关闭所有单元

基本范例 (3)

Haar 小波函数：

Daubechies 小波函数：

墨西哥帽状（Mexican hat）小波函数：

范围 (5)

计算原始小波函数：

对偶小波函数：

包括 HaarWavelet 的离散小波的小波函数：

DaubechiesWavelet:

CoifletWavelet:

BiorthogonalSplineWavelet:

ReverseBiorthogonalSplineWavelet:

ShannonWavelet:

BattleLemarieWavelet:

包括 DGaussianWavelet 的连续小波的小波函数：

MexicanHatWavelet:

ShannonWavelet:

多元尺度和小波函数是单变量的乘积：

选项 (3)

MaxRecursion (1)

使用不同程度的递归绘制小波函数：

WorkingPrecision (2)

默认情况下，使用 WorkingPrecision->MachinePrecision：

使用高精度滤波计算：

属性和关系 (4)

小波函数积分为零：

满足递归方程：

绘制元件与递归和：

的频响由给出：

该滤波器为高通滤波器：

的傅立叶变换由给出：

巧妙范例 (1)

绘制小波函数的平移和伸缩：

顶部