WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

WaveletPsi

✖
WaveletPsi[wave,x]

gives the wavelet function for the symbolic wavelet wave evaluated at x.

✖
WaveletPsi[wave]

gives the wavelet function as a pure function.

Details and Options

  • The wavelet function 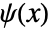satisfies the recursion equation 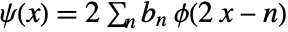, where 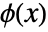is the scaling function and 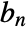are the high-pass filter coefficients.
  • A discrete wavelet transform effectively represents a signal 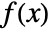in terms of scaled and translated wavelet functions 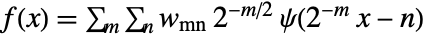, where .
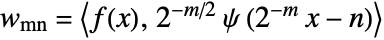  • WaveletPsi[wave,x,"Dual"] gives the dual wavelet function 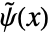for biorthogonal wavelets such as BiorthogonalSplineWavelet and ReverseBiorthogonalSplineWavelet.
  • The dual wavelet function satisfies the recursion equation 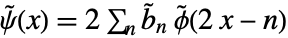, where 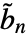are the dual high-pass filter coefficients.
  • The following options can be used:
  • MaxRecursion 8number of recursive iterations to use
    WorkingPrecision MachinePrecisionprecision to use in internal computations

Examples

open allclose all

Basic Examples  (3)Summary of the most common use cases

Haar wavelet function:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-b0xj5n
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-exatgm
Out[2]=2

Daubechies wavelet function:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-vc7o0g
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-xdbxfp
Out[2]=2

Mexican hat wavelet function:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-rgea5u
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-s8s5w4
Out[2]=2

Scope  (5)Survey of the scope of standard use cases

Compute primal wavelet function:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-34r0y7
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-jrnvtl
Out[2]=2

Dual wavelet function:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-rqnscj
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-wgpsnb
Out[2]=2

Wavelet function for discrete wavelets, including HaarWavelet:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-5qil82
Out[1]=1

DaubechiesWavelet:

In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-8a3e1y
Out[2]=2

SymletWavelet:

In[3]:=3
✖
https://wolfram.com/xid/0mlijs723ho4-6m8se7
Out[3]=3

CoifletWavelet:

In[4]:=4
✖
https://wolfram.com/xid/0mlijs723ho4-uikmj
Out[4]=4

BiorthogonalSplineWavelet:

In[5]:=5
✖
https://wolfram.com/xid/0mlijs723ho4-slohlo
Out[5]=5

ReverseBiorthogonalSplineWavelet:

In[6]:=6
✖
https://wolfram.com/xid/0mlijs723ho4-isy48o
Out[6]=6

CDFWavelet:

In[7]:=7
✖
https://wolfram.com/xid/0mlijs723ho4-m6y6cq
Out[7]=7

ShannonWavelet:

In[8]:=8
✖
https://wolfram.com/xid/0mlijs723ho4-cylqwd
Out[8]=8

BattleLemarieWavelet:

In[9]:=9
✖
https://wolfram.com/xid/0mlijs723ho4-2pig47
Out[9]=9

MeyerWavelet:

In[10]:=10
✖
https://wolfram.com/xid/0mlijs723ho4-tg8sc8
Out[10]=10

Wavelet function for continuous wavelets, including DGaussianWavelet:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-z43vp5
Out[1]=1

MexicanHatWavelet:

In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-08gn4g
Out[2]=2

GaborWavelet:

In[3]:=3
✖
https://wolfram.com/xid/0mlijs723ho4-l7ss7d
Out[3]=3

ShannonWavelet:

In[4]:=4
✖
https://wolfram.com/xid/0mlijs723ho4-dp3dkk
Out[4]=4

MorletWavelet:

In[5]:=5
✖
https://wolfram.com/xid/0mlijs723ho4-rvmw1f
Out[5]=5

PaulWavelet:

In[6]:=6
✖
https://wolfram.com/xid/0mlijs723ho4-w8vkr0
Out[6]=6

Multivariate scaling and wavelet functions are products of univariate ones:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-s2egvc
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-tvf11
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mlijs723ho4-yf2o9
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0mlijs723ho4-s16yjj
Out[4]=4
In[5]:=5
✖
https://wolfram.com/xid/0mlijs723ho4-gmiius
Out[5]=5

Options  (3)Common values & functionality for each option

MaxRecursion  (1)

Plot wavelet function using different levels of recursion:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-hjxsba
Out[1]=1

WorkingPrecision  (2)

By default WorkingPrecision->MachinePrecision is used:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-ec0mf7
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-3ruht5
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mlijs723ho4-qtqwdb
Out[3]=3

Use higher-precision filter computation:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-oxpk71
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-f6wruc
Out[2]=2

Properties & Relations  (4)Properties of the function, and connections to other functions

Wavelet function integrates to zero :

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-wzkw5n
Out[1]=1

satisfies the recursion equation :

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-3enc2f
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-bux40a

Plot the components and the sum of the recursion:

In[3]:=3
✖
https://wolfram.com/xid/0mlijs723ho4-4clwfm
In[4]:=4
✖
https://wolfram.com/xid/0mlijs723ho4-p99dtx
Out[4]=4

Frequency response for is given by :

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-fujnuf

The filter is a high-pass filter:

In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-s5vizp
Out[2]=2

Fourier transform of is given by :

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-4ndhmw
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-8z0zd4
In[3]:=3
✖
https://wolfram.com/xid/0mlijs723ho4-hyy32u
In[4]:=4
✖
https://wolfram.com/xid/0mlijs723ho4-f7zvgz
Out[4]=4

Neat Examples  (1)Surprising or curious use cases

Plot translates and dilations of wavelet function:

In[1]:=1
✖
https://wolfram.com/xid/0mlijs723ho4-iu0uje
In[2]:=2
✖
https://wolfram.com/xid/0mlijs723ho4-b9ooxs
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0mlijs723ho4-hts69i
Out[3]=3
Wolfram Research (2010), WaveletPsi, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletPsi.html.
✖
Wolfram Research (2010), WaveletPsi, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletPsi.html.

Text

Wolfram Research (2010), WaveletPsi, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletPsi.html.

✖
Wolfram Research (2010), WaveletPsi, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletPsi.html.

CMS

Wolfram Language. 2010. "WaveletPsi." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletPsi.html.

✖
Wolfram Language. 2010. "WaveletPsi." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletPsi.html.

APA

Wolfram Language. (2010). WaveletPsi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletPsi.html

✖
Wolfram Language. (2010). WaveletPsi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletPsi.html

BibTeX

@misc{reference.wolfram_2025_waveletpsi, author="Wolfram Research", title="{WaveletPsi}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletPsi.html}", note=[Accessed: 23-June-2025 ]}

✖
@misc{reference.wolfram_2025_waveletpsi, author="Wolfram Research", title="{WaveletPsi}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletPsi.html}", note=[Accessed: 23-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_waveletpsi, organization={Wolfram Research}, title={WaveletPsi}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletPsi.html}, note=[Accessed: 23-June-2025 ]}

✖
@online{reference.wolfram_2025_waveletpsi, organization={Wolfram Research}, title={WaveletPsi}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletPsi.html}, note=[Accessed: 23-June-2025 ]}