ZipfDistribution

ZipfDistribution[ρ]

母数 ρ のゼータ分布を表す．

ZipfDistribution[n,ρ]

範囲 n のZipf分布を表す．

詳細

  • ZipfDistribution[ρ]は離散パレート分布としても知られている．
  • ZipfDistribution[n,ρ]はEstoup分布としても知られている．
  • 値 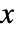と有限な 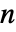の確率は x^(-(rho+1))/TemplateBox[{n, {rho, +, 1}}, HarmonicNumber2]で与えられる．無限の 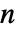については x^(-(rho+1))/TemplateBox[{{rho, +, 1}}, Zeta]で与えられる．
  • ZipfDistributionでは，ρ は任意の正の実数でよく，n は任意の正の整数でよい．
  • ZipfDistributionは，Mean，CDF，RandomVariate等の関数で使うことができる． »

予備知識

  • ZipfDistribution[n,ρ]は，整数値 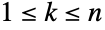について定義され，正の実数 ρ および正の整数 n （分布の範囲）によって決定される離散統計分布を表す．Zipf分布の確率密度関数(PDF)は離散的で単調減少であり，その全体的な形（広がり，領域，傾斜が急かどうか）は母数 ρ および n の値によって決まる．ここで定義しているZipf分布はEstoup分布と呼ばれることがある．母数が1つの形のZipfDistribution[ρ]は n→∞ ときのZipfDistribution[n,ρ]の極限に等しく，最も一般的なZipf分布であるが，ゼータ分布，Zipfian分布，離散パレート分布（連続ParetoDistributionと混同してはならない）等と呼ばれることもある．
  • Zipf分布はアメリカ人の言語学者George Zipfに因んで名付けられた．Zipfは1930年代から1940年代にかけて行動と心理についての自身の研究にこの分布を盛んに応用した．この分布は，フランス人の速記者であるBaptiste Estoupによってすでに1912年から同様の文脈で応用されていたが，Zipfの研究によってZipf分布が基礎となっている現在Zipfの法則と呼ばれるものが誕生した．この法則は，自然言語における任意の単語の使用頻度は，度数分布と関連したその言語におけるその語の順位と反比例すると述べている．このため，現代におけるZipf分布の応用分野は言語学および意味論関連が多くなっている．しかし，この分布は数論，生物学，経済学においても使用されている．
  • RandomVariateを使って，Zipf分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,ZipfDistribution[n,ρ]]（より簡略な表記では xZipfDistribution[n,ρ]）を使って，確率変数 x がZipf分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[ZipfDistribution[n,ρ],x]およびCDF[ZipfDistribution[n,ρ],x]を使って得られる．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．これらの数量はDiscretePlotを使って可視化できる．
  • DistributionFitTestを使って，与えられたデータ集合がZipf分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックZipf分布を推定することが，FindDistributionParametersを使ってデータをZipf分布にフィットすることができる．ProbabilityPlotを使って記号Zipf分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号Zipf分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたZipf分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってZipf分布を含む高次元分布を構築することが，ProductDistributionを使ってZipf分布を含む独立成分分布の結合分布を計算することができる．
  • ZipfDistributionは他の数多くの統計分布と関連がある．この分布は，しばしばParetoDistributionの離散バージョンであるとみなされ，したがって，PowerDistribution，StableDistribution，ExponentialDistribution，PearsonDistribution，BetaPrimeDistributionと関係がある．ZipfDistributionは，CauchyDistribution，LevyDistribution，PoissonDistribution，PoissonConsulDistribution，SkellamDistributionとも関連している．

例題

すべて開くすべて閉じる

例  (4)

確率質量関数：

有限範囲で：

累積分布関数：

有限範囲で：

平均：

分散：

スコープ  (7)

Zipf分布から擬似乱数のサンプルを生成する：

そのヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度：

歪度がその最小値に達する位置を求める：

範囲 n で：

尖度：

尖度がその最小値に達する位置を求める：

範囲 n で：

母数の関数としての閉形式の種々のモーメント：

Moment：

Momentは閉形式である：

範囲 n で：

記号次数の閉形式：

CentralMoment：

範囲 n で：

FactorialMoment：

範囲 n で：

Cumulant：

範囲 n で：

ハザード関数：

範囲 n で：

分位関数：

範囲 n で：

アプリケーション  (6)

ZipfDistributionのCDFは右連続関数の例である：

あるテキストの単語数がZipf分布に従う：

ZipfDistributionを単語頻度のデータにフィットする：

頻度ヒストグラムを推定分布と比較する：

ある単語が10回より多く使われる確率を求める：

単語の平均使用回数を求める：

人気度によって15のWebページに順位を付ける．アクセス頻度は のZipf分布に従う．アクセス頻度の分布を求める：

一番人気のあるサイトがリクエストされる確率を求める：

11位から15位までのサイトのリクエスト確率を求める：

30回の独立したリクエストのシミュレーションを行う：

あるオンラインの映画レンタルサイトには2000本の映画があり，人気の高いものはキャッシュを保存してより迅速に提供できるようになっている．リクエストした映画がキャッシュされている確率が0.99になるためにキャッシュする必要がある映画の最低数を求める：

ZipfDistributionを使って乱数間のGCDの分布をモデル化することができる：

ランダムなサンプルを作る：

Zipf分布をデータにフィットする：

Zipf分布をデータの範囲でフィットする：

サンプルのヒストグラムを両方の推定分布と比較する：

対数尤度を比較する：

有限範囲の条件で分布統計が著しく変わる：

標準偏差も変わる：

中央値は等しい：

テロリストの攻撃による死傷者数はZipfDistributionに従う：

Zipf分布をデータにフィットする：

データのヒストグラムを推定分布の確率密度関数と比較する：

特性と関係  (7)

正の整数以外の実数を得る確率は零である：

確率質量と確率変数にはベキ法則の関係がある：

Zipf分布における最初の値に対する 番目の値の相対頻度は のベキ乗である：

極限では，2番目の値が最初の値のの頻度，3番目の値は最初の値のの頻度という具合になる：

Zipf分布は切断のもとで閉じている：

範囲がある場合：

他の分布との関係：

両方のZipf分布が極限で同じになる：

Khintchineの無限に分割可能なリーマン(Riemann)のゼータ分布は，ZipfDistributionに関連している：

ζ の特性関数がリーマンのゼータ関数の期待される比であることを確認する：

考えられる問題  (2)

ZipfDistributionは，ρ が正ではない場合は定義されない：

記号出力に無効な母数値を代入すると意味のない結果となる：

Wolfram Research (2007), ZipfDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ZipfDistribution.html （2010年に更新）.

テキスト

Wolfram Research (2007), ZipfDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/ZipfDistribution.html （2010年に更新）.

CMS

Wolfram Language. 2007. "ZipfDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2010. https://reference.wolfram.com/language/ref/ZipfDistribution.html.

APA

Wolfram Language. (2007). ZipfDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ZipfDistribution.html

BibTeX

@misc{reference.wolfram_2024_zipfdistribution, author="Wolfram Research", title="{ZipfDistribution}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/ZipfDistribution.html}", note=[Accessed: 22-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_zipfdistribution, organization={Wolfram Research}, title={ZipfDistribution}, year={2010}, url={https://reference.wolfram.com/language/ref/ZipfDistribution.html}, note=[Accessed: 22-November-2024 ]}