ToBoundaryMesh[r]
generates a boundary ElementMesh object from the boundary of a region r.
ToBoundaryMesh[r,{{xmin,xmax},…}]
generates a boundary ElementMesh object from the boundary of a region r restricted to the bounding box ![]() .
.
ToBoundaryMesh[rules]
generates a boundary ElementMesh object from a set of rules specifying coordinates and boundary elements.
ToBoundaryMesh[emesh]
generates a new boundary ElementMesh object from an existing ElementMesh, MeshRegion, or BoundaryMeshRegion.




ToBoundaryMesh
ToBoundaryMesh[r]
generates a boundary ElementMesh object from the boundary of a region r.
ToBoundaryMesh[r,{{xmin,xmax},…}]
generates a boundary ElementMesh object from the boundary of a region r restricted to the bounding box ![]() .
.
ToBoundaryMesh[rules]
generates a boundary ElementMesh object from a set of rules specifying coordinates and boundary elements.
ToBoundaryMesh[emesh]
generates a new boundary ElementMesh object from an existing ElementMesh, MeshRegion, or BoundaryMeshRegion.
更多信息和选项
- ToBoundaryMesh[r] generates a boundary ElementMesh object that approximates the boundary of the possibly symbolic region r. In a boundary ElementMesh, the "MeshElements" are set to Automatic and can be computed by using ToElementMesh.
- The specification for regions includes objects described by geometric regions and ImplicitRegion.
- The region r should be a constant region for which ConstantRegionQ gives True.
- In ToBoundaryMesh[rules], the following rules should be given in this order:
-
"Coordinates"->{c1,c2,…} required to specify the coordinates to be c1, c2, … "BoundaryElements"->{b1,…} required to specify the boundary elements in the mesh to be b1, … "PointElements"->{p1,…} optionally specify the point elements in the mesh to be p1, … - For a 1D boundary element mesh, "BoundaryElements" are PointElement.
- For a 2D boundary element mesh, "BoundaryElements" are LineElement.
- For a 3D boundary element mesh, "BoundaryElements" can be TriangleElement and QuadElement.
- ToBoundaryMesh[emesh] may be used to modify an ElementMesh object emesh in various ways, including extracting the boundary and adding markers.
- ToBoundaryMesh has the following options:
-
AccuracyGoal Infinity digits of accuracy sought "BoundaryGroupingThreshold" Automatic control the grouping of boundaries by normal direction "BoundaryMarkerFunction" None function to compute markers for boundary elements "BoundaryMeshGenerator" Automatic function to generate boundary ElementMesh "CheckIntersections" Automatic control testing for intersecting boundaries "DeleteDuplicateCoordinates" True delete duplicate coordinates "IncludePoints" {} points to be included and considered part of the boundary "MaxBoundaryCellMeasure" Automatic control the size of boundary elements MaxCellMeasure Automatic control the size of mesh elements "MeshOrder" Automatic order of the element mesh "MessageHead" Automatic symbol for messages "PointMarkerFunction" None function to compute markers for point elements PrecisionGoal Automatic digits of precision sought "RegionHoles" Automatic specify region holes - With MaxCellMeasure->m, the measure of the cells created in the region dimension d will be at most m. The measure for the d-1-dimensional boundary representation cells will by default be chosen to be compatible with good quality d-dimensional cells with measure m. Limits for specific dimensions may be specified by using MaxCellMeasure->{"Volume"->v,"Area"->a,"Length"->l}.
- With AccuracyGoal->a and PrecisionGoal->p, an attempt will be made to keep the maximum distance between the region r or the discretized region dreg and any point in RegionSymmetricDifference[r,dreg] to less than
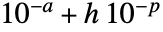 , where
, where 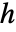 is the length of the diagonal of the bounding box.
is the length of the diagonal of the bounding box. - ToBoundaryMesh[bmesh,opts] or ToBoundaryMesh[emesh,opts] may be used to modify a boundary ElementMesh object bmesh or extract the boundary from a full ElementMesh object emesh in various ways by specifying any one of the options to ToBoundaryMesh.
- If ToBoundaryMesh cannot generate an ElementMesh, then $Failed is returned.
- Invoking ToBoundaryMesh on an EmptyRegion will return an EmptyRegion.
- Options given to ToBoundaryMesh can be given to NDSolve by specifying "MeshOptions". »
- Setting options for ToBoundaryMesh from NDSolve and related functions is explained in NDSolve Finite Element Options.
范例
打开所有单元 关闭所有单元基本范例 (4)
Create a boundary element mesh of a Disk:
Convert the boundary element mesh to a full mesh:
Create a boundary mesh of a union of a Disk and a Rectangle:
Create a boundary mesh by explicitly specifying the boundary elements:
Create a full element mesh from the boundary mesh and visualize the resulting element mesh:
Scope (15)
Generate a boundary mesh of a Disk:
Convert an ImplicitRegion with an explicit bounding box:
Convert a GraphicsComplex to a boundary element mesh:
Convert a TransformedRegion to a boundary element mesh:
Convert a 3D Ball to a boundary element mesh:
Convert a 3D GraphicsComplex to a boundary element mesh:
Convert a 3D TransformedRegion to a boundary element mesh:
Create a boundary element mesh from four coordinates and one boundary element:
For a set of points, ToBoundaryMesh will return the convex hull:
1D Point Element Boundary Meshes (2)
2D Line Element Boundary Meshes (1)
Boundary Markers (1)
Boundary markers are useful to specify NeumannValue on a region boundary and are explained further in the section Markers in the Element Mesh Generation.
Create a rectangle with boundary element markers and one additional node inside the domain:
Point Markers (1)
Point markers are useful to specify DirichletCondition on a region boundary and are explained further in the section Markers in the Element Mesh Generation.
Create a rectangle with a boundary element and point elements with markers and one additional node inside the domain:
Visualize the point elements in the boundary mesh with node numbers in blue and markers in red:
Options (26)
"AccuracyGoal" (1)
"BoundaryGroupingThreashold" (7)
ToBoundaryMesh automatically attributes markers to groups of contiguous boundary segments by comparing the boundary normal vectors.
Create a boundary mesh from the numerical region:
Inspect the boundary element markers present:
Visualize the contiguous boundaries:
Visualize the boundaries with element marker 2 or 4:
Inspect the point element markers present:
Use the element markers for specifying boundary conditions in NDSolveValue:
DirichletCondition extracts the point element markers, while NeumannValue and PeriodicBoundaryCondition extract boundary element markers.
Point element markers (red) are deduced from boundary markers (blue). If the node's connected boundary element markers are the same, then the node will have the same marker. On corners, the connected boundary markers typically differ, and an arbitrary choice of the available markers is made:
To control the behavior of which marker gets assigned to a corner node, a "PointMarkerFunction" can be specified. In the following case, all nodes on the left get a 2 as a marker, and on the right get a 4. The remaining markers are deduced from the boundary segment markers:
Switch off the automatic boundary grouping:
The only boundary element marker is the default of 0:
The automatic boundary grouping chooses boundary segments to be contiguous by computing the normals of the boundary segments and then computing the dot product of the neighboring segments. When the dot product is above a threshold ![]() , the neighboring segments are considered contiguous.
, the neighboring segments are considered contiguous.
Create a coarse boundary mesh where boundary elements are grouped if the threshold ![]() :
:
Inspect the union of the boundary element markers:
Create a coarse boundary mesh where boundary elements are grouped if the threshold ![]() :
:
Inspect the union of the boundary element markers:
Construct a 1D boundary mesh with an internal boundary:
The boundary elements include the internal boundary at 1.0 (index 2):
In 1D, the boundary normal for an interior boundary is taken to be 0:
Inspect the union of boundary element markers:
Create a boundary element mesh in 3D from a discretized graphic:
Generate a list of colors for the many boundary groups:
Visualize only the boundaries with element marker 1:
Inspect the boundaries with a different element marker:
The automatic boundary grouping can be useful even for complicated geometries with a large number of groups. Import a gear as an element mesh:
Visualize the boundary mesh and the contiguous boundary groups:
"BoundaryMarkerFunction" (1)
Boundary markers are useful to specify NeumannValue on a region boundary and are explained further in the section Markers in the Element Mesh Generation.
Here is a function that computes integer markers for edges, depending on the coordinates of the edge elements:
Visualize the boundary mesh and the boundary markers:
Inspect the boundary elements:
If "PointElementMarkers" are also computed, those are accessible as the second argument in the function given to "BoundaryMarkerFunction".
"BoundaryMeshGenerator" (7)
The "Continuation" method uses a curve continuation method that can in many cases resolve corners, cusps, and sharp changes quite well:
The "RegionPlot" method is based on improving output from RegionPlot and can sometimes be faster:
The "RegionPlot" method has suboptions to improve the quality of the boundary mesh:
Pass a method option to the BoundaryDiscretizeRegion boundary mesh generator:
Pass a method option to the BoundaryDiscretizeRegion boundary mesh generator to fine-tune the discretization algorithm:
Visualize the boundary mesh as a mesh region:
The "OpenCascade" boundary mesh generator is well suited for 3D BooleanRegion expressions consisting of Graphics3D primitives.
Use "OpenCascade" as a boundary mesh generator:
Generate colors for the boundary markers:
Visualize the boundary element mesh with highlighted boundary markers:
Replace the internal boundary mesh generator with a custom mesh generator:
"DeleteDuplicateCoordinates" (2)
"IncludePoints" (1)
Specify some additional points to be included in the boundary mesh:
Include the points in the boundary mesh:
Visualize the boundary mesh with the included points:
These additional points are considered to be part of the boundary, but need not be on the actual boundary.
Create the full mesh from the numerical region:
Points added with "IncludePoints" will be addressable with DirichletCondition. Additionally, if the predicate in DirichletCondition is True, then the boundary condition will take effect at the include points.
"MaxBoundaryCellMeasure" (2)
"MaxCellMeasure" (2)
With MaxCellMeasure->m, a cell size is chosen and a boundary cell size is set to be appropriate for good-quality cells in the embedding dimension:
A specific length can be specified using MaxCellMeasure->{"Length"->len}:
A helper function to compute the length of the boundary segments:
"MeshOrder" (1)
ToBoundaryMesh by default generates a first-order boundary mesh:
Integrate over the boundary mesh and assess the accuracy of the integration:
To obtain a second-order boundary mesh, the option "MeshOrder" may be used:
Integrate over the boundary mesh and assess the accuracy of the integration:
More information about the "MeshOrder" option can be found in this section of the Element Mesh Generation tutorial and this section of the Element Mesh Generation tutorial.
"PointMarkerFunction" (1)
Point markers are useful to specify DirichletCondition on a region boundary and are explained further in the section Markers in the Element Mesh Generation.
Here is a function that computes integer markers for point elements, depending on the coordinates of the edge nodes:
Properties & Relations (1)
Pass options for ToBoundaryMesh to NDSolve to solve a stationary PDE:
Possible Issues (5)
If the input symbolic region is unbounded, a default bounding box from ![]() is assumed in each space direction:
is assumed in each space direction:
By specifying an explicit bounding box, the default can be overridden:
Sometime boundary features may not be resolved well:
Setting the size of the boundary elements and increasing the sample points may help:
Alternatively, the "Continuation" boundary mesh generator may work better:
Specifying "IncludePoints" that lie on the boundary of the specified region can create boundary meshes that cannot be converted to full meshes:
The specified "IncludePoints" need to be inside the region:
The amount by which the "IncludePoints" need to be inside the region depends on accuracy of the curvature of the mesh.
The arguments to ToBoundaryMesh are specified as rules and need to be given in the correct order: "Coordinates", "BoundaryElements" and optionally "PointElements":
相关指南
文本
Wolfram Research (2014),ToBoundaryMesh,Wolfram 语言函数,https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html (更新于 2021 年).
CMS
Wolfram 语言. 2014. "ToBoundaryMesh." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html.
APA
Wolfram 语言. (2014). ToBoundaryMesh. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html 年
BibTeX
@misc{reference.wolfram_2025_toboundarymesh, author="Wolfram Research", title="{ToBoundaryMesh}", year="2021", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_toboundarymesh, organization={Wolfram Research}, title={ToBoundaryMesh}, year={2021}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html}, note=[Accessed: 06-February-2026]}