BesagL

BesagL[pdata,r]

estimates Besag's function for point data pdata at radius r.

BesagL[pproc,r]

computes for the point process pproc.

BesagL[bdata,r]

computes for binned data bdata.

BesagL[pspec]

generates the function that can be applied repeatedly to different radii r.

Details and Options

  • BesagL is a transformation of the RipleyK function that makes it easier to compare to a completely spatially random reference process.
  • BesagL 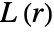is defined as 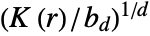, where 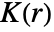is RipleyK, 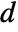is the spatial dimension, and 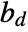is the volume of a unit ball in .
  •     
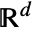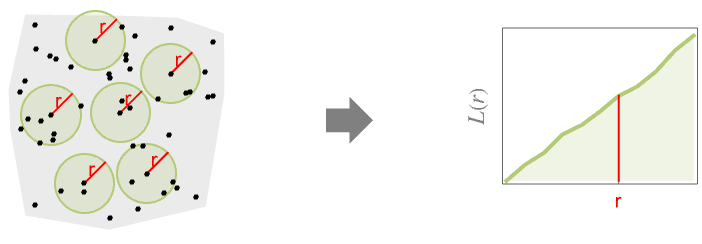
  • BesagL measures spatial homogeneity of a point collection within distance r. Comparing with a Poisson point process gives:
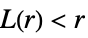
  • more dispersed than Poisson
    like Poisson, i.e. complete spatial randomness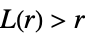
    more clustered than Poisson
  •     
  • The radius r can be a single value or a list of values. With no radius r specified, BesagL returns a PointStatisticFunction that can be used to evaluate the 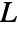function repeatedly.
  • The points pdata can have the following forms:
  • {p1,p2,…}points pi
    GeoPosition[…],GeoPositionXYZ[…],…geographic points
    SpatialPointData[…]spatial point collection
    {pts,reg}point collection pts and observation region reg
  • If the observation region reg is not given, a region is automatically computed using RipleyRassonRegion.
  • The point process pproc can have the following forms:
  • proca point process proc
    {proc,reg}a point process proc and observation region reg
  • The observation region reg should be parameter free and SpatialObservationRegionQ.
  • The binned data bdata is from SpatialBinnedPointData and is treated as an InhomogeneousPoissonPointProcess with a piecewise constant density function.
  • For pdata, is computed by counting distinct pairs of points within distance r of each other.
  • For pproc, 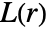is computed by using exact formulas or by simulation to generate point data.
  • The following options can be given:
  • MethodAutomaticwhat methods to use
    SpatialBoundaryCorrection Automaticwhat boundary correction to use
  • The following settings can be used for SpatialBoundaryCorrection:
  • Automaticautomatically determined boundary correction
    Noneno boundary correction
    "BorderMargin"use interior margin for observation region
    "Ripley"uses weights depending on the point distance to boundary

Examples

open allclose all

Basic Examples  (3)

Estimate Besag's function at a given distance:

Estimate Besag's function within a range of distances:

Visualize the result with ListPlot:

Besag's function of a cluster point process:

Visualize the function with given parameter values:

Scope  (10)

Point Data  (5)

Estimate Besag's function at distance 0.2:

Obtain empirical estimates of Besag's function from a list of given distances:

Use BesagL with SpatialPointData:

Create a PointStatisticFunction for future use:

Estimate Besag's function without explicitly providing the observation region:

Observation region generated by Ripley–Rasson estimator:

Estimated function at distance 0.3:

Use BesagL with GeoPosition:

Plot the point statistics function:

Point Processes  (5)

Besag's function for PoissonPointProcess does not depend on the density or the dimension:

Besag's function for a cluster process ThomasPointProcess with specified dimension:

In 3D:

Besag's function for a cluster process MaternPointProcess with specified dimension:

In 3D:

Besag's function for a cluster process CauchyPointProcess:

Besag's function for a cluster process VarianceGammaPointProcess:

Options  (2)

SpatialBoundaryCorrection  (2)

The BesagL estimator without boundary correction is biased and should not be used unless with a large point set:

The default method "BorderMargin" only considers the points that are distance from the boundary:

Boundary correction method "Ripley" weights each pair of points to make the estimator unbiased:

Compare different edge correction methods:

Estimate the values of Besag's function with three different methods:

Visualize the results and compare to the theoretical value:

Applications  (5)

Besag's function is cumulative in the distance and hence monotone increasing:

Besag's function for complete spatial randomness:

Compute Besag's function for few dimensions:

Visualize the results:

Points in a hardcore point process cannot be closer than the hard-core radius :

Estimate the values of Besag's function:

Visualize the results:

Find hard-core radii estimates for the three samples:

Besag's of clustered data is higher than complete spatially random data. Sample from a cluster process:

Generate a control sample from a Poisson point process with the same intensity:

Compare the Besag's functions:

Use Besag's function to estimate PairCorrelationG:

Pair correlation from data:

Compute Besag's function:

Estimate pair correlation:

Compare the estimate with the pair correlation computed from the data:

Properties & Relations  (1)

BesagL is the variance-stabilized RipleyK: , where is Ripley's function, is the spatial dimension and is the volume of a unit ball in :

Possible Issues  (1)

Empirical BesagL with border correction may not be increasing (especially for smaller sets):

The uncorrected BesagL is increasing:

Wolfram Research (2020), BesagL, Wolfram Language function, https://reference.wolfram.com/language/ref/BesagL.html.

Text

Wolfram Research (2020), BesagL, Wolfram Language function, https://reference.wolfram.com/language/ref/BesagL.html.

CMS

Wolfram Language. 2020. "BesagL." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BesagL.html.

APA

Wolfram Language. (2020). BesagL. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BesagL.html

BibTeX

@misc{reference.wolfram_2024_besagl, author="Wolfram Research", title="{BesagL}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/BesagL.html}", note=[Accessed: 18-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_besagl, organization={Wolfram Research}, title={BesagL}, year={2020}, url={https://reference.wolfram.com/language/ref/BesagL.html}, note=[Accessed: 18-November-2024 ]}