BetaDistribution[α,β]
形状母数 α と β の連続型のベータ分布を表す.


BetaDistribution
BetaDistribution[α,β]
形状母数 α と β の連続型のベータ分布を表す.
詳細
- ベータ分布における値
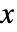 の確率密度は,
の確率密度は,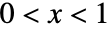 では
では 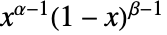 に比例し,
に比例し,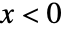 または
または 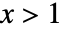 の場合はゼロとなる. »
の場合はゼロとなる. » - BetaDistributionでは,α および β は任意の正の実数でよい.
- BetaDistributionでは,α と β は無次元量でよい. »
- BetaDistributionは,Mean,CDF,RandomVariate等の関数で使うことができる. »
予備知識
- BetaDistribution[α,β]は,区間
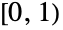 上で定義され,「形状母数」として知られる2つの正の値 α および β でパラメータ化される統計分布を表す.この形状母数が確率密度関数(PDF)の右裾部と左裾部のいわゆる「太り具合」を決定する.ベータ分布のPDFは,α と β の値によって,単調増加であったり,単調減少であったり,潜在的な特異値がその領域の境界に接近する,単一の「峰」を持ったりする.
上で定義され,「形状母数」として知られる2つの正の値 α および β でパラメータ化される統計分布を表す.この形状母数が確率密度関数(PDF)の右裾部と左裾部のいわゆる「太り具合」を決定する.ベータ分布のPDFは,α と β の値によって,単調増加であったり,単調減少であったり,潜在的な特異値がその領域の境界に接近する,単一の「峰」を持ったりする. - ベータ分布は,ベイズ解析における二項比率についての事前分布として起る.これは,一般に,有限区間に限定された確率変数をモデル化するためにも使われる.例えば,連続独立一様分布に従うサイズ
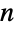 のサンプルの
のサンプルの 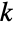
 番目に小さい要素の分布は,OrderDistribution[{UniformDistribution[],n},k]を使って計算することができ,BetaDistribution[k,n-k+1]と厳密に等しい.ベータ分布は,その統計的有意性に加え,対立遺伝子頻度分布に関連する現象,土質の変動性,地質学における鉱物含有率,HIVの感染挙動等,数多くの科学分野で基本的な役割を果たす.
番目に小さい要素の分布は,OrderDistribution[{UniformDistribution[],n},k]を使って計算することができ,BetaDistribution[k,n-k+1]と厳密に等しい.ベータ分布は,その統計的有意性に加え,対立遺伝子頻度分布に関連する現象,土質の変動性,地質学における鉱物含有率,HIVの感染挙動等,数多くの科学分野で基本的な役割を果たす. - RandomVariateを使って,ベータ分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,BetaDistribution[α,β]](より簡略な表記では xBetaDistribution[α,β])を使って,確率変数 x がベータ分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BetaDistribution[α,β],x]およびCDF[BetaDistribution[α,β],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がベータ分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからパラメトリックベータ分布を推定することが,FindDistributionParametersを使ってデータをベータ分布にフィットすることができる.ProbabilityPlotを使って記号ベータ分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ベータ分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたベータ分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってベータ分布を含む高次元分布を構築することが,ProductDistributionを使ってベータ分布を含む独立成分分布の結合分布を計算することができる.
- ベータ分布は他の数多くの分布と関連している.例えば,BetaDistributionは,BernoulliDistribution,BinomialDistribution,NegativeBinomialDistribution,GeometricDistributionを含む他の多くの分布についてのいわゆる「共役事前確率分布」である.さらに,BetaDistributionは,PDF[BetaDistribution[1,1],x]がPDF[UniformDistribution[],x]とPDF[PowerDistribution[1,1],x]の両方と等しいという意味(端点
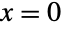 および
および 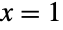 を含んで法として)において,UniformDistributionとPowerDistributionの両方を一般化する.BetaDistributionはKumaraswamyDistributionおよびNoncentralBetaDistributionの変換としても得ることができ,PERTDistribution,PearsonDistribution,ChiSquareDistribution,GammaDistribution,FRatioDistribution,BetaPrimeDistributionと密接な関係がある.
を含んで法として)において,UniformDistributionとPowerDistributionの両方を一般化する.BetaDistributionはKumaraswamyDistributionおよびNoncentralBetaDistributionの変換としても得ることができ,PERTDistribution,PearsonDistribution,ChiSquareDistribution,GammaDistribution,FRatioDistribution,BetaPrimeDistributionと密接な関係がある.
例題
すべて開く すべて閉じるスコープ (8)
サンプルの密度ヒストグラムを推定された分布の確率密度関数と比較する:
極限では,尖度はNormalDistributionのものと同じになる:
母数でQuantityを一貫して用いると,母数がその数値に拡張される:
アプリケーション (3)
ある特定の地域では,曇っている時間が母数を0.3と0.4としたベータ分布にほぼ従う.曇りが半日以上続く確率を求める:
1日のうちの曇っている時間の割合のシミュレーションを30日間分行う:
1ヶ月間で曇っている時間が10%より少ない日がちょうど20日間になる確率を求める:
1ヶ月間で曇っている時間が10%より少ない日が少なくとも20日になる確率を求める:
ベータ分布は指定の1日に株価が上昇した株の割合のモデルに使うことができる.ベータ分布をダウ平均株価にフィットする:
ダウ平均株価の株式の少なくとも60%の株価が上昇する確率を求める:
ダウ平均株価の株式で30日間に渡って株価が上昇するものの割合のシミュレーションを行う:
離散時間マルコフ連鎖 ![]() (ただし,
(ただし,![]() は同一同分布に従う一連の標準一様確率変数で,
は同一同分布に従う一連の標準一様確率変数で,![]() は独立同分布に従う成功確率が
は独立同分布に従う成功確率が ![]() のベルヌーイ確率変数)は,
のベルヌーイ確率変数)は,![]() である任意の初期条件
である任意の初期条件 ![]() について定常分布BetaDistribution[p,1-p]に収束する:
について定常分布BetaDistribution[p,1-p]に収束する:
このマルコフ連鎖の実現からサンプルを取り,経路のバーンイン部分を除去する:
マルコフ連鎖からのサンプルは独立ではなく,内部構造を示している:
経路の値のヒストグラムをマルコフ連鎖の定常分布PDFと比較する:
特性と関係 (21)
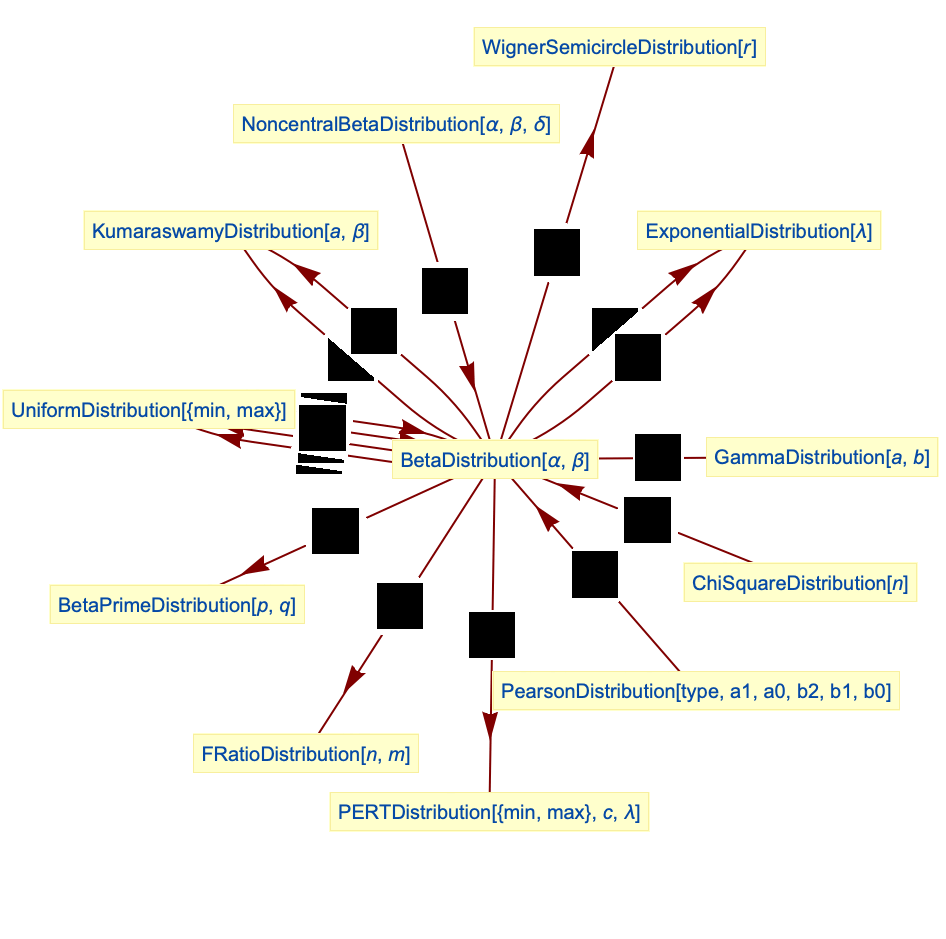
BetaDistribution[1,1]はUniformDistribution[{0,1}]に等しい:
BetaDistributionはUniformDistributionを変換したものである:
UniformDistributionはBetaDistributionを変換したものである:
BetaDistributionはNoncentralBetaDistributionの極限のケースである:
BetaPrimeDistributionはベータ分布に従う変数を変換して得ることができる:
ベータ分布はタイプ1のPearsonDistributionの特殊ケースである:
ベータ分布はGammaDistributionの変換として得ることができる:
ベータ分布はChiSquareDistributionを変換したものとして求めることができる:
FRatioDistributionはベータ分布から求めることができる:
ベータ分布はUniformDistributionに従っている変数の次数分布である:
ExponentialDistributionはスケールされたベータ分布の極限である:
ExponentialDistributionはベータ分布を変換したものである:
KumaraswamyDistributionはベータ分布を変換したものである:
KumaraswamyDistributionを簡約するとベータ分布の特殊なケースになる:
PERTDistributionはベータ分布を変換したものである:
WignerSemicircleDistributionは特殊ベータ分布の変換である:
DirichletDistributionの一変量周辺分布はベータ分布である:
BetaBinomialDistributionはBinomialDistributionとBetaDistributionを混合したものである:
BetaNegativeBinomialDistributionはNegativeBinomialDistributionとBetaDistributionを混合したものである:
考えられる問題 (2)
テクニカルノート
-
▪
- 連続分布
関連するガイド
-
▪
- 有界領域分布 ▪
- パラメトリック統計分布 ▪
- 統計学で使用される関数
テキスト
Wolfram Research (2007), BetaDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BetaDistribution.html (2016年に更新).
CMS
Wolfram Language. 2007. "BetaDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BetaDistribution.html.
APA
Wolfram Language. (2007). BetaDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BetaDistribution.html
BibTeX
@misc{reference.wolfram_2025_betadistribution, author="Wolfram Research", title="{BetaDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BetaDistribution.html}", note=[Accessed: 14-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_betadistribution, organization={Wolfram Research}, title={BetaDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BetaDistribution.html}, note=[Accessed: 14-January-2026]}