BetaPrimeDistribution
形状母数が p と q のベータプライム分布を表す.
BetaPrimeDistribution[p,q,β]
尺度母数が β の一般化されたベータプライム分布を表す.
BetaPrimeDistribution[p,q,α,β]
形状母数が α の一般化された第2種ベータ分布を表す.
詳細
- BetaPrimeDistribution[1,q,1,β]はLomax分布としても知られている.
- ベータプライム分布中の値
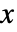 の確率密度は
の確率密度は 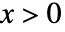 のとき
のとき 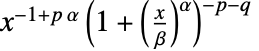 に比例する.
に比例する. - BetaPrimeDistributionでは,p,q,α,β は任意の正の実数でよい.
- BetaPrimeDistributionでは,β は任意の単位次元の数量でよく,p,q,α は無次元量でよい. »
- BetaPrimeDistributionは,Mean,CDF,RandomVariate等の関数とともに使うことができる.
予備知識
- BetaPrimeDistribution[p,q,α,β]は,区間
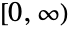 上で定義され,4つの正の実数 p,q,α,β でパラメータ化された連続統計分布を表す.母数 p,q,α は「形状母数」として知られ,β は「尺度母数」として知られるものである.これらの母数はベータプライム分布の確率密度関数(PDF)の全体的な形を決定する.p,q,α,β の値によって,ベータプライム分布のPDFは,単峰性か潜在的な特異値が領域の下限に近付いていく単調減少になる.加えて,PDFの裾部はPDFが,
上で定義され,4つの正の実数 p,q,α,β でパラメータ化された連続統計分布を表す.母数 p,q,α は「形状母数」として知られ,β は「尺度母数」として知られるものである.これらの母数はベータプライム分布の確率密度関数(PDF)の全体的な形を決定する.p,q,α,β の値によって,ベータプライム分布のPDFは,単峰性か潜在的な特異値が領域の下限に近付いていく単調減少になる.加えて,PDFの裾部はPDFが,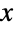 の大きい値について指数的にではなく代数的に減少するという意味で「厚い」.(この動作は,分布のSurvivalFunctionを分析することで数量的に厳密にできる.)
の大きい値について指数的にではなく代数的に減少するという意味で「厚い」.(この動作は,分布のSurvivalFunctionを分析することで数量的に厳密にできる.) - BetaPrimeDistribution[p,q,α,β]は,一般化された第2種ベータ分布,逆ベータ分布,タイプ6のピアソン分布(PearsonDistribution)と呼ばれることがある.2引数および3引数形のBetaPrimeDistribution[p,q]およびBetaPrimeDistribution[p,q,β]を評価すると,それぞれBetaPrimeDistribution[p,q,1,1]およびBetaPrimeDistribution[p,q,1,β]となる.これらはそれぞれ,標準ベータプライム分布,一般化されたベータプライム分布と呼ばれることがある.
- ベイズ解析では,ベータプライム分布は,確率として表現された二項比率についての事前分布として登場している.ベータプライム分布は,現実世界の多くの現象をモデル化することも分かっている.例えば,ベータプライム分布は,証券利益の経験的予測やオプションプライスモデルの開発に役立つことが証明されている.より近年には,保険の損失過程のモデリングに適用されている.他にも,ベータプライム分布の長い裾部は,この分布が個人集団の中で疾病を伝染させやすい動作頻度とそのような疾病の実際の伝染のモデル化に特に適していることを示している.
- RandomVariateを使ってたベータプライム分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,BetaPrimeDistribution[p,q,α,β]](より簡略すると xBetaPrimeDistribution[p,q,α,β])を使って,確率変数 x がベータプライム分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BetaPrimeDistribution[p,q,α,β],x]およびCDF[BetaPrimeDistribution[p,q,α,β],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がベータプライム分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからベータプライムパラメトリック分布を推定することが,FindDistributionParametersを使ってデータをベータプライム分布にフィットすることができる.ProbabilityPlotを使って記号ベータプライム分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号ベータプライム分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたベータプライム分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってベータプライム分布を含む高次元分布を構築することが,ProductDistributionを使ってベータプライム分布を含む独立成分分布の結合分布を計算することができる.
- BetaPrimeDistributionは他の多くの分布と関係がある.例えば,BetaPrimeDistribution[p,q,a,b]は,
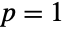 のときに簡約するとDagumDistribution[p,a,b]になり,
のときに簡約するとDagumDistribution[p,a,b]になり,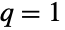 で簡約するとSinghMaddalaDistribution[q,a,b] になる.
で簡約するとSinghMaddalaDistribution[q,a,b] になる.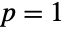 および
および 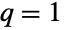 ではLogLogisticDistribution[a,b]になる.これに加え,2つの母数を持つ形のBetaPrimeDistribution[p,q]はタイプ6のピアソン分布PearsonDistribution[6,1,f/g,1/g,1/g,0](
ではLogLogisticDistribution[a,b]になる.これに加え,2つの母数を持つ形のBetaPrimeDistribution[p,q]はタイプ6のピアソン分布PearsonDistribution[6,1,f/g,1/g,1/g,0](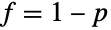 および
および 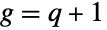 )と同じPDFを有し,タイプIIとタイプIVの両ParetoDistributionと関連している.BetaPrimeDistributionのPDFはBetaDistributionのPDFを変換したものであるのに対し,4引数の形BetaPrimeDistribution[p,q,a,1]は,2つの独立確率変数XGammaDistribution[p,1,a,0]および YGammaDistribution[q,1,a,0]の商
)と同じPDFを有し,タイプIIとタイプIVの両ParetoDistributionと関連している.BetaPrimeDistributionのPDFはBetaDistributionのPDFを変換したものであるのに対し,4引数の形BetaPrimeDistribution[p,q,a,1]は,2つの独立確率変数XGammaDistribution[p,1,a,0]および YGammaDistribution[q,1,a,0]の商 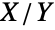 である.BetaPrimeDistributionは,FRatioDistribution,DirichletDistribution,KumaraswamyDistribution,NoncentralBetaDistribution,PERTDistributionとも関連がある.
である.BetaPrimeDistributionは,FRatioDistribution,DirichletDistribution,KumaraswamyDistribution,NoncentralBetaDistribution,PERTDistributionとも関連がある.
例題
すべて開くすべて閉じる例 (12)
スコープ (9)
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
一般化された第2種ベータ分布では,歪度は β に依存しない:
一般化された第2種ベータ分布では,尖度は β に依存しない:
パラメータでQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (2)
BetaPrimeDistributionは損失のモデル化に使用できる:
明らかな外れ値である最も被害の大きかったハリケーンAndrewを除く:
これから来る強力な30のハリケーンで被り得る損失のシミュレーションを,単位を百万USドルとして行う:
BetaPrimeDistributionを使って州ごとの1人あたりの収入をモデル化することができる:
特性と関係 (16)
一般化された第2種ベータ分布の累積分布関数に対する母数の影響:
BetaPrimeDistributionは正の因子によるスケーリングの下では閉じている:
BetaPrimeDistributionは,逆数を取る下では閉じている:
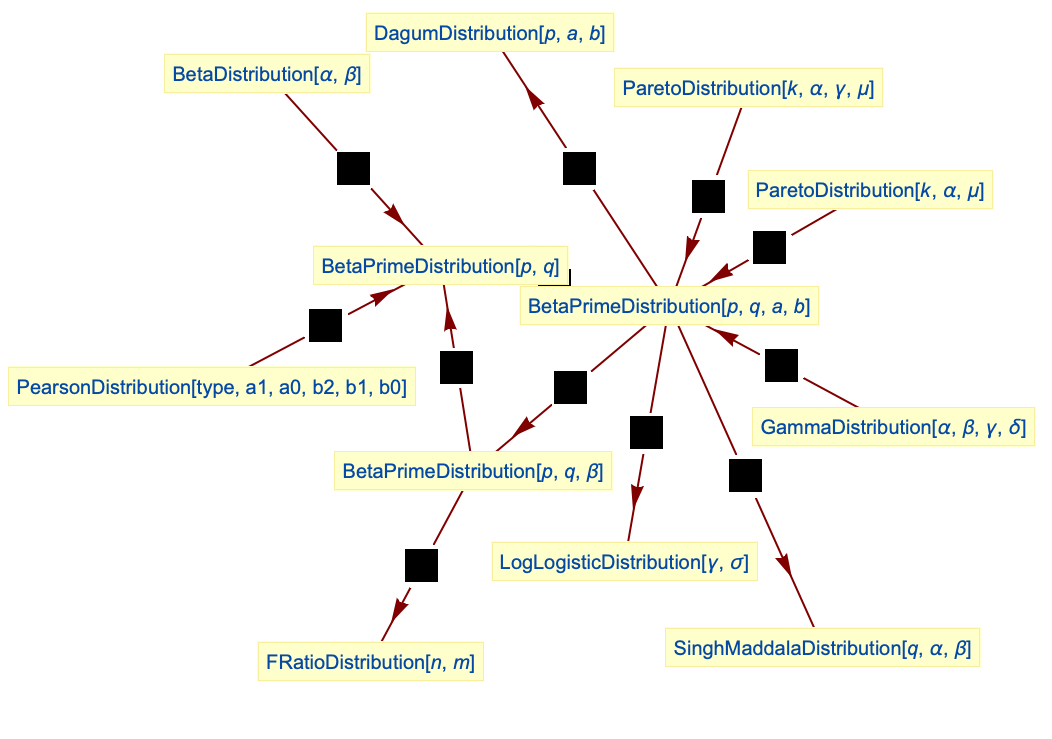
DagumDistributionはBetaPrimeDistributionの特殊ケースである:
SinghMaddalaDistributionはBetaPrimeDistributionの特殊ケースである:
LogLogisticDistributionはBetaPrimeDistributionの特殊ケースである:
FRatioDistributionはBetaPrimeDistributionの特殊ケースである:
ベータプライム分布はタイプ6のPearsonDistributionの特殊ケースである:
タイプIIのParetoDistributionはBetaPrimeDistributionに関連している:
タイプIVのParetoDistributionはBetaPrimeDistributionに関連している:
ベータプライム分布は BetaDistributionを変換して求めることができる:
一般化された第2種ベータ分布は,GammaDistributionの2つの独立した確率変数の比の分布である:
一般化された第2種ベータ分布を簡約するとベータプライム分布になる:
テキスト
Wolfram Research (2010), BetaPrimeDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BetaPrimeDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "BetaPrimeDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BetaPrimeDistribution.html.
APA
Wolfram Language. (2010). BetaPrimeDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BetaPrimeDistribution.html