BirnbaumSaundersDistribution[α,λ]
represents the Birnbaum–Saunders distribution with shape parameter α and scale parameter λ.


BirnbaumSaundersDistribution
BirnbaumSaundersDistribution[α,λ]
represents the Birnbaum–Saunders distribution with shape parameter α and scale parameter λ.
Details
- The cumulative distribution function for value
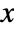 in a Birnbaum–Saunders distribution is given by
in a Birnbaum–Saunders distribution is given by 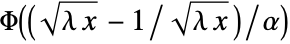 , where
, where 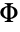 is the CDF for the standard normal distribution.
is the CDF for the standard normal distribution. - BirnbaumSaundersDistribution allows α and λ to be any positive real numbers.
- BirnbaumSaundersDistribution allows λ to be a quantity of any unit dimension, and α to be a dimensionless quantity. »
- BirnbaumSaundersDistribution can be used with such functions as Mean, CDF, and RandomVariate.
Background & Context
- BirnbaumSaundersDistribution[α,λ] represents a continuous statistical distribution defined over the interval
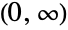 and parametrized by two positive values α and λ. Here, α is known as a "shape parameter," γ is a so-called "scale parameter," and together these parameters determine various properties of the probability density function (PDF), including its height and its horizontal location in the plane. The PDF of the Birnbaum–Saunders distribution is unimodal and has "thin tails" in the sense that the PDF decreases exponentially for large values
and parametrized by two positive values α and λ. Here, α is known as a "shape parameter," γ is a so-called "scale parameter," and together these parameters determine various properties of the probability density function (PDF), including its height and its horizontal location in the plane. The PDF of the Birnbaum–Saunders distribution is unimodal and has "thin tails" in the sense that the PDF decreases exponentially for large values 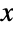 . (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.)
. (This behavior can be made quantitatively precise by analyzing the SurvivalFunction of the distribution.) - The Birnbaum–Saunders distribution dates back to the late 1960s to the work of mathematicians Z. W. Birnbaum and S. C. Saunders and was originally proposed as a lifetime model for materials subject to cyclic patterns of stress and strain. Also known as the fatigue-life distribution, the Birnbaum–Saunders distribution is still actively used to model life cycles in manufacturing. More recently, modified versions of the distribution have been used to accurately model the distribution of mineral concentration in drinking water. Elsewhere, the distribution has been used to approximate the quantile function of the inverse Gaussian distribution (InverseGaussianDistribution), to perform analyses in various areas of engineering science, and to model certain biological processes subject to rapid decline.
- RandomVariate can be used to give one or more machine- or arbitrary-precision (the latter via the WorkingPrecision option) pseudorandom variates from a Birnbaum–Saunders distribution. Distributed[x,BirnbaumSaundersDistribution[α,λ]], written more concisely as xBirnbaumSaundersDistribution[α,λ], can be used to assert that a random variable x is distributed according to a Birnbaum–Saunders distribution. Such an assertion can then be used in functions such as Probability, NProbability, Expectation, and NExpectation.
- The probability density and cumulative distribution functions may be given using PDF[BirnbaumSaundersDistribution[α,λ],x] and CDF[BirnbaumSaundersDistribution[α,λ],x]. The mean, median, variance, raw moments, and central moments may be computed using Mean, Median, Variance, Moment, and CentralMoment, respectively.
- DistributionFitTest can be used to test if a given dataset is consistent with a Birnbaum–Saunders distribution, EstimatedDistribution to estimate a Birnbaum–Saunders parametric distribution from given data, and FindDistributionParameters to fit data to a Birnbaum–Saunders distribution. ProbabilityPlot can be used to generate a plot of the CDF of given data against the CDF of a symbolic Birnbaum–Saunders distribution and QuantilePlot to generate a plot of the quantiles of given data against the quantiles of a symbolic Birnbaum–Saunders distribution.
- TransformedDistribution can be used to represent a transformed Birnbaum–Saunders distribution, CensoredDistribution to represent the distribution of values censored between upper and lower values, and TruncatedDistribution to represent the distribution of values truncated between upper and lower values. CopulaDistribution can be used to build higher-dimensional distributions that contain a Birnbaum–Saunders distribution, and ProductDistribution can be used to compute a joint distribution with independent component distributions involving beta distributions.
- The Birnbaum–Saunders distribution is related to a number of other distributions. For example, given a random variate
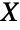 , XBirnbaumSaundersDistribution[α,γ] if and only if YNormalDistribution[] where
, XBirnbaumSaundersDistribution[α,γ] if and only if YNormalDistribution[] where 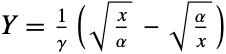 . Visually, the PDF of BirnbaumSaundersDistribution tends to appear "bell-shaped," thereby introducing qualitative relationships with a number of other distributions, including CauchyDistribution, StudentTDistribution, and LogisticDistribution. BirnbaumSaundersDistribution is also related to LogNormalDistribution, BetaDistribution, and JohnsonDistribution.
. Visually, the PDF of BirnbaumSaundersDistribution tends to appear "bell-shaped," thereby introducing qualitative relationships with a number of other distributions, including CauchyDistribution, StudentTDistribution, and LogisticDistribution. BirnbaumSaundersDistribution is also related to LogNormalDistribution, BetaDistribution, and JohnsonDistribution.
Examples
open all close allBasic Examples (4)
Scope (8)
Generate a sample of pseudorandom numbers from a Birnbaum–Saunders distribution:
Compare its histogram to the CDF:
Distribution parameters estimation:
Estimate the distribution parameters from sample data:
Compare the density histogram of the sample with the PDF of the estimated distribution:
Skewness depends only on the shape parameter α:
Kurtosis depends only on the shape parameter α:
Different moments with closed forms as functions of parameters:
Closed form for symbolic order:
Closed form for symbolic order:
Consistent use of Quantity in parameters yields QuantityDistribution:
Applications (3)
The lifetime in hours of a component has a Birnbaum–Saunders distribution with ![]() and
and ![]() per hour. Find the probability the component survives 300 hours:
per hour. Find the probability the component survives 300 hours:
Find the probability that the component is still working after 500 hours, after it has survived 300 hours:
Find the mean time to failure:
Simulate the failure times for 30 independent components like this:
The time to failure of component A follows a Birnbaum–Saunders distribution with ![]() and
and ![]() per hour, while the failure rate of component B is 1 per hour. Find the mean time to failure for both components:
per hour, while the failure rate of component B is 1 per hour. Find the mean time to failure for both components:
Find the probability that component A fails before component B:
Although they have the same mean lifetime, a Birnbaum–Saunders distribution tends to fail early:
The lifetime of a device has a Birnbaum–Saunders distribution. Find the reliability of the device:
The hazard function has horizontal asymptote ![]() :
:
Find the reliability of two such devices in series:
Properties & Relations (3)
Birnbaum–Saunders distribution is closed under scaling by a positive factor:
If ![]() has a Birnbaum–Saunders distribution, then
has a Birnbaum–Saunders distribution, then ![]() also has a Birnbaum–Saunders distribution:
also has a Birnbaum–Saunders distribution:
Birnbaum–Saunders distribution is related to NormalDistribution:
Related Guides
Text
Wolfram Research (2010), BirnbaumSaundersDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/BirnbaumSaundersDistribution.html (updated 2016).
CMS
Wolfram Language. 2010. "BirnbaumSaundersDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BirnbaumSaundersDistribution.html.
APA
Wolfram Language. (2010). BirnbaumSaundersDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BirnbaumSaundersDistribution.html
BibTeX
@misc{reference.wolfram_2025_birnbaumsaundersdistribution, author="Wolfram Research", title="{BirnbaumSaundersDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/BirnbaumSaundersDistribution.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_birnbaumsaundersdistribution, organization={Wolfram Research}, title={BirnbaumSaundersDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/BirnbaumSaundersDistribution.html}, note=[Accessed: 03-March-2026]}