BirnbaumSaundersDistribution
BirnbaumSaundersDistribution[α,λ]
形状母数 α,尺度母数 λ のBirnbaum–Saunders分布を表す.
詳細
- Birnbaum–Saunders分布における値
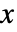 の累積分布関数は
の累積分布関数は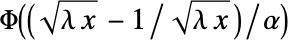 で与えられる.ただし,
で与えられる.ただし,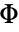 は標準正規分布の累積分布関数(CDF)を表す.
は標準正規分布の累積分布関数(CDF)を表す. - BirnbaumSaundersDistributionでは,α と λ は任意の正の実数でよい.
- BirnbaumSaundersDistributionでは,λ は任意の単位次元の数量でよく,α は無次元量でよい. »
- BirnbaumSaundersDistributionは,Mean,CDF,RandomVariate等の関数とともに用いることができる.
予備知識
- BirnbaumSaundersDistribution[α,λ]は,区間
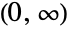 上で定義され,2つの正の値 α および λ でパラメータ化された連続統計分布を表す.α は「形状母数」として知られ,γ は「尺度母数」として知られているものであり,両者が一緒になって,高さや平面上の水平位置等,確率密度関数(PDF)のさまざまな特性を決定する.Birnbaum–Saunders分布のPDFは,単峰性で,PDFが
上で定義され,2つの正の値 α および λ でパラメータ化された連続統計分布を表す.α は「形状母数」として知られ,γ は「尺度母数」として知られているものであり,両者が一緒になって,高さや平面上の水平位置等,確率密度関数(PDF)のさまざまな特性を決定する.Birnbaum–Saunders分布のPDFは,単峰性で,PDFが 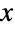 の大きい値について指数関数的に減少するという意味で「薄い裾部」を持つ.(この動作は,分布のSurvivalFunctionを分析することで数量的に厳密にすることができる.)
の大きい値について指数関数的に減少するという意味で「薄い裾部」を持つ.(この動作は,分布のSurvivalFunctionを分析することで数量的に厳密にすることができる.) - Birnbaum–Saunders分布は,もともとは,1960年代の後半に,数学者のZ.W. BirnbaumとS.C. Saundersによって,応力と歪みの周期性パターンに影響される物質の寿命モデルとして提案された.Birnbaum–Saunders分布は,疲労寿命分布としても知られており,現在も製造業における寿命サイクルのモデル化に盛んに使われている.より最近になって,この分布の修正バージョンが,飲料水におけるミネラル濃度の分布の正確なモデル化に使われるようになった.この他では,この分布は逆ガウス分布(InverseGaussianDistribution)の分位関数の近似,工業科学のさまざまな分野における分析,急速な低下の影響を受けるある種の生物学過程のモデル化等に使われている.
- RandomVariateを使ってBirnbaum–Saunders分布から,1つあるいは複数の機械精度あるいは任意精度(後者はWorkingPrecisionオプションを介す)の擬似乱数変量を得ることができる.Distributed[x,BirnbaumSaundersDistribution[α,λ]](より簡略すると xBirnbaumSaundersDistribution[α,λ])を使って,確率変数 x がBirnbaum–Saunders分布に従って分布していると宣言することができる.このような宣言は,Probability,NProbability,Expectation,NExpectation等の関数で使うことができる.
- 確率密度関数および累積分布関数は,PDF[BirnbaumSaundersDistribution[α,λ],x]およびCDF[BirnbaumSaundersDistribution[α,λ],x]を使って得られることがある.平均,中央値,分散,原点の周りのモーメント,中心モーメントは,それぞれMean,Median,Variance,Moment,CentralMomentを使って計算することができる.
- DistributionFitTestを使って,与えられたデータ集合がBirnbaum–Saunders分布と一致するかどうかを検定することが,EstimatedDistributionを使って与えられたデータからBirnbaum–Saundersパラメトリック分布を推定することが,FindDistributionParametersを使ってデータをBirnbaum–Saunders分布にフィットすることができる.ProbabilityPlotを使って記号Birnbaum–Saunders分布のCDFに対する与えられたデータのCDFのプロットを生成することが,QuantilePlotを使って記号Birnbaum–Saunders分布の変位値に対する与えられたデータの変位値のプロットを生成することができる.
- TransformedDistributionを使って変換されたBirnbaum–Saunders分布を表すことが,CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが,TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる.CopulaDistributionを使ってBirnbaum–Saunders分布を含む高次元分布を構築することが,ProductDistributionを使ってBirnbaum–Saunders分布を含む独立成分分布の結合分布を計算することができる.
- Birnbaum–Saunders分布は他の多くの分布に関連している.例えば,確率変量
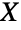 を与えられた場合,YNormalDistribution[]である場合かつその場合に限り XBirnbaumSaundersDistribution[α,γ]である.ただし,
を与えられた場合,YNormalDistribution[]である場合かつその場合に限り XBirnbaumSaundersDistribution[α,γ]である.ただし,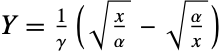 である.視覚的には,BirnbaumSaundersDistributionのPDFは「ベルの形」に見えることが多く,したがって,CauchyDistribution,StudentTDistribution,LogisticDistributionを含む他の多くの関数との定性的関係を導く.BirnbaumSaundersDistributionはLogNormalDistribution,BetaDistribution,JohnsonDistributionとも関係がある.
である.視覚的には,BirnbaumSaundersDistributionのPDFは「ベルの形」に見えることが多く,したがって,CauchyDistribution,StudentTDistribution,LogisticDistributionを含む他の多くの関数との定性的関係を導く.BirnbaumSaundersDistributionはLogNormalDistribution,BetaDistribution,JohnsonDistributionとも関係がある.
例題
すべて開くすべて閉じるスコープ (8)
Birnbaum–Saunders分布から擬似乱数のサンプルを生成する:
サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する:
母数でQuantityを一貫して使うとQuantityDistributionが与えられる:
アプリケーション (3)
ある部品の寿命を時間単位で表すと,1時間あたり ![]() ,
,![]() のBirnbaum–Saunders分布に従うとする.この部品が300時間以上使える確率を求める:
のBirnbaum–Saunders分布に従うとする.この部品が300時間以上使える確率を求める:
この部品が寿命の300時間を超え500時間以上経ってもまだ使える確率を求める:
これと類似する独立した30個の部品の故障までの時間のシミュレーションを行う:
部品Aの故障までの時間は1時間あたり ![]() ,
,![]() のBirnbaum–Saundersに従い,部品Bの故障率は1時間あたり1であるとして,この両方の部品の故障までの平均時間を求める:
のBirnbaum–Saundersに従い,部品Bの故障率は1時間あたり1であるとして,この両方の部品の故障までの平均時間を求める:
両者の平均寿命は同じだが,Birnbaum–Saunders分布に従う方が早く故障する率が高い:
特性と関係 (3)
Birnbaum–Saunders分布は正の因子によるスケーリングの下では閉じている:
![]() がBirnbaum–Saunders分布に従うなら,
がBirnbaum–Saunders分布に従うなら,![]() もまたBirnbaum–Saunders分布に従う:
もまたBirnbaum–Saunders分布に従う:
Birnbaum–Saunders分布はNormalDistributionに関連している:
テキスト
Wolfram Research (2010), BirnbaumSaundersDistribution, Wolfram言語関数, https://reference.wolfram.com/language/ref/BirnbaumSaundersDistribution.html (2016年に更新).
CMS
Wolfram Language. 2010. "BirnbaumSaundersDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/BirnbaumSaundersDistribution.html.
APA
Wolfram Language. (2010). BirnbaumSaundersDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BirnbaumSaundersDistribution.html