CompleteKaryTree

CompleteKaryTree[n]

n レベルの完全二分木を与える．

CompleteKaryTree[n,k]

n レベルの完全 k 分木を与える．

詳細とオプション

CompleteKaryTreeは完全な k 分木としても知られている．
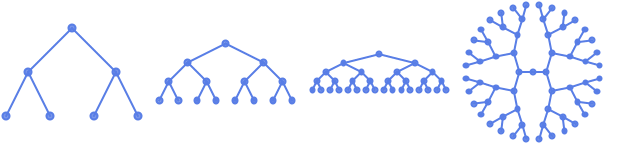
n レベルの完全 k 分木は各ノードのブランチ数が k，深さが n レベルの有根木である．

n レベルの完全 k 分木には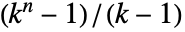個の頂点がある．
CompleteKaryTree[…,DirectedEdges->True]は有向完全 k 分木を与える．
CompleteKaryTreeにはGraphと同じオプションが使える．

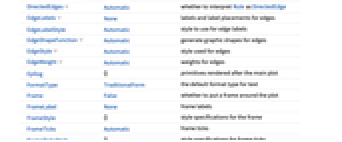
全オプションのリスト

AlignmentPoint	Center	整列の基準となるグラフィックス内のデフォルトの点
AnnotationRules	{}	グラフ，辺，頂点の注釈
AspectRatio	Automatic	縦横比
Axes	False	座標軸を描くか描かないか
AxesLabel	None	座標軸のラベル
AxesOrigin	Automatic	座標軸の交点
AxesStyle	{}	座標軸のスタイル指定
Background	None	プロットの背景色
BaselinePosition	Automatic	周囲のテキストのベースラインとの揃え方
BaseStyle	{}	グラフィックスのベーススタイル指定
ContentSelectable	Automatic	コンテンツの選択を許容するかどうか
CoordinatesToolOptions	Automatic	座標ツールの細かな動作
DirectedEdges	Automatic	RuleをDirectedEdgeとして解釈するかどうか
EdgeLabels	None	辺のラベルとその置き方
EdgeLabelStyle	Automatic	辺のラベルのスタイル
EdgeShapeFunction	Automatic	辺のグラフィックス形状を生成する
EdgeStyle	Automatic	辺のスタイル
EdgeWeight	Automatic	辺の重み
Epilog	{}	主となるプロットの後に描くプリミティブ
FormatType	TraditionalForm	テキストのデフォルトの書式
Frame	False	プロットの周囲に枠を描くか描かないか
FrameLabel	None	枠のラベル
FrameStyle	{}	枠線のスタイル指定
FrameTicks	Automatic	枠の目盛
FrameTicksStyle	{}	枠目盛のスタイル指定
GraphHighlight	{}	ハイライトするグラフ要素
GraphHighlightStyle	Automatic	ハイライトするスタイル
GraphLayout	Automatic	辺と頂点をどのように配置するか
GridLines	None	描画する格子線
GridLinesStyle	{}	格子線のスタイル指定
ImageMargins	0.	グラフィックスの周囲に残す余白
ImagePadding	All	ラベル等に余分な充填をどの程度許すか
ImageSize	Automatic	描画するグラフィックスの絶対的サイズ
LabelStyle	{}	ラベルのスタイル指定
Method	Automatic	使用するグラフィックスメソッドの詳細
PerformanceGoal	Automatic	パフォーマンスのどの面について最適化するか
PlotLabel	None	全体的なプロットのラベル
PlotRange	All	含める値の範囲
PlotRangeClipping	False	プロット範囲で切り取るかどうか
PlotRangePadding	Automatic	値の範囲をどの程度充填するか
PlotRegion	Automatic	塗り潰す最終的な表示領域
PlotTheme	$PlotTheme	グラフの全体的なテーマ
PreserveImageOptions	Automatic	同じ画像を新たに描画する際に画像のもとのオプションを保存するかどうか
Prolog	{}	主となるプロットに先駆けて描かれるプリミティブ
RotateLabel	True	枠の y 軸に与えられているラベルを回転させるかどうか
Ticks	Automatic	座標軸の目盛
TicksStyle	{}	座標軸の目盛のスタイル指定
VertexCoordinates	Automatic	頂点座標
VertexLabels	None	頂点のラベルとその置き方
VertexLabelStyle	Automatic	頂点ラベルのスタイル
VertexShape	Automatic	頂点のグラフィックスの形状
VertexShapeFunction	Automatic	頂点のグラフィックス形状を生成する
VertexSize	Medium	頂点の大きさ
VertexStyle	Automatic	頂点のスタイル
VertexWeight	Automatic	頂点の重み

例題

すべて開くすべて閉じる

例 (3)

5レベルの完全二分木：

3レベルの完全三分木：

有向辺を使う：

オプション (79)

AnnotationRules (2)

頂点の注釈を指定する：

辺の注釈を指定する：

DirectedEdges (1)

デフォルトで，無向グラフが生成される：

DirectedEdges->Trueを使って有向グラフを生成する：

EdgeLabels (6)

辺12にラベルを付ける：

すべての辺に別々にラベルを付ける：

任意の式をラベルとして使う：

明示的な座標を使ってラベルを置く：

ラベル内の位置を変える：

複数のラベルを置く：

TooltipとStatusAreaからの値で自動的にラベルを付ける：

EdgeShapeFunction (6)

EdgeShapeFunctionの組込み設定のリストを得る：

基線を含む無向辺：

辺に異なるグリフを持つ線：

塗り潰された矢印を含む有向辺：

線の矢印：

塗り潰されていない矢印：

個々の辺の辺関数を指定する：

別のデフォルトの辺関数と組み合せる：

プログラムを実行して辺を描画する：

EdgeShapeFunctionはEdgeStyleと組み合せることができる：

EdgeShapeFunctionはEdgeStyleより優先順位が高い：

EdgeStyle (2)

辺にスタイルを付ける：

個々の辺にスタイルを付ける：

EdgeWeight (2)

すべての辺の重みを指定する：

任意の数式を重みとして使う：

GraphLayout (5)

デフォルトで，レイアウトは自動的に選ばれる：

特殊な曲線の上のレイアウトを指定する：

最適化の基準を満たすレイアウトを指定する：

VertexCoordinatesはGraphLayoutの座標を無効にする：

AbsoluteOptionsを使ってレイアウトアルゴリズムで計算されたVertexCoordinatesを抽出する：

GraphHighlight (3)

頂点1をハイライトする：

辺13をハイライトする：

頂点と辺をハイライトする：

GraphHighlightStyle (2)

GraphHighlightStyleの組込み設定のリストを得る：

GraphHighlightStyleの組込み設定を使う：

PlotTheme (4)

基本テーマ (2)

一般的な基本テーマを使う：

白黒のテーマを使う：

特徴テーマ (2)

大きいグラフのテーマを使う：

古典的な図表テーマを使う：

VertexCoordinates (3)

デフォルトで，任意の頂点座標が自動的に計算される：

AbsoluteOptionsを使って結果の頂点座標を抽出する：

楕円に沿ったレイアウト関数を指定する：

これを使ってグラフの頂点座標を生成する：

VertexCoordinatesはGraphLayoutより優先順位が高い：

VertexLabels (13)

頂点名をラベルとして使う：

個々の頂点にラベルを付ける：

すべての頂点にラベルを付ける：

任意の式をラベルとして使う：

Placedを記号位置と一緒に使って外側位置を含むラベル配置を制御する：

記号的外側コーナー位置：

記号的内側位置：

記号的内側コーナー位置：

明示的な座標を使ってラベルの中心を置く：

すべてのラベルを頂点の右上コーナー位置に置き，ラベル内の座標を変化させる：

複数のラベルを置く：

任意の数のラベルを使うことができる：

Placedの引数を使ってTooltipを含むフォーマットを制御する：

あるいはStatusAreaを含むフォーマットを制御する：

より高度なフォーマット関数を使う：

VertexShape (5)

Graphics，ImageあるいはGraphics3Dを頂点の形に使う：

個々の頂点の形を指定する：

VertexShapeはVertexSizeと組み合せることができる：

VertexShapeはVertexStyleの影響を受けない：

VertexShapeFunctionはVertexShapeより優先順位が高い：

VertexShapeFunction (10)

組込みのVertexShapeFunctionコレクションのリストを得る：

"Basic"コレクションのVertexShapeFunctionの組込み設定を使う：

簡単な基本形：

一般的な基本形：

"Rounded"コレクションのVertexShapeFunction：

"Concave"コレクションのVertexShapeFunctionの組込み設定を使う：

個々の頂点を描画する：

デフォルトの頂点関数と組み合せる：

定義済みのグラフィックスを使って頂点を描画する：

プログラムを実行して頂点を描画する：

VertexShapeFunctionはVertexStyleと組み合せることができる：

VertexShapeFunctionはVertexStyleより優先順位が高い：

VertexShapeFunctionはVertexSizeと組み合せることができる：

VertexShapeFunctionはVertexShapeより優先順位が高い：

VertexSize (8)

デフォルトで，頂点の大きさは自動的に計算される：

記号的な頂点サイズを使ってすべての頂点の大きさを指定する：

頂点座標間の最短距離との比を使う：

すべての頂点座標に全体的な対角との比を使う：

方向と方向の両方の大きさを指定する：

個々の頂点の大きさを指定する：

VertexSizeはVertexShapeFunctionと組み合せることができる：

VertexSizeはVertexShapeと組み合せることができる：

VertexStyle (5)

すべての頂点にスタイルを付ける：

個々の頂点にスタイルを付ける：

VertexShapeFunctionはVertexStyleと組み合せることができる：

VertexShapeFunctionはVertexStyleより優先順位が高い：

VertexStyleはBaseStyleと組み合せることができる：

VertexStyleはBaseStyleより優先順位が高い：

VertexShapeはVertexStyleの影響を受けない：

VertexWeight (2)

すべての頂点について重みを設定する：

任意の数式を重みとして使う：

アプリケーション (7)

完全 k 分木のGraphCenter：

GraphPeriphery：

VertexEccentricity：

頂点離心率経路をハイライトする：

GraphRadius：

半径経路をハイライトする：

GraphDiameter：

直径経路をハイライトする：

CompleteKaryTreeの頂点次数をハイライトする：

接近中心性をハイライトする：

固有ベクトル中心性をハイライトする：

からまでの頂点連結性はからまでの頂点独立経路の数である：

木の頂点連結性はすべての頂点ペアについて1である：

特性と関係 (8)

CompleteKaryTree[n,k]にはの頂点がある：

CompleteKaryTree[n,k]にはの辺がある：

頂点が個の完全 k 分木にはの辺がある：

完全 k 分木は木グラフである：

完全 k 分木は二部グラフである：

完全 k 分木は非巡回グラフである：

完全 k 分木にはループがない：

完全 k 分木は k 分木の特殊ケースである：

トップへ