DiscretizeRegion[reg]
領域 reg をMeshRegionに離散化する.
DiscretizeRegion[reg,{{xmin,xmax},…}]
境界![]() に制限する.
に制限する.




DiscretizeRegion
DiscretizeRegion[reg]
領域 reg をMeshRegionに離散化する.
DiscretizeRegion[reg,{{xmin,xmax},…}]
境界![]() に制限する.
に制限する.
詳細とオプション

- DiscretizeRegionは,メッシュ生成あるいは格子生成としても知られている.
- DiscretizeRegionは,領域 reg の内側と境界を離散化する.
- 特に,DiscretizeRegionは reg のより次元の低い部分を離散化しようとする.
- 領域 reg はConstantRegionQでRegionEmbeddingDimensionが3以下のものなら何でもよい.
- DiscretizeRegionには,MeshRegionと同じオプションに以下の追加・変更を加えたものが使える.
-
AccuracyGoal Automatic 目標とする確度桁数 MaxCellMeasure Automatic 最大セル測度 MeshQualityGoal Automatic メッシュセルの品質目標 Method Automatic 使用するメソッド MeshRefinementFunction None メッシュセルのより細かな分割が必要な場合にTrueを返す関数 PerformanceGoal $PerformanceGoal スピードまたは品質を考慮するかどうか PrecisionGoal Automatic 目標とする精度桁数 - MeshRefinementFunction->f とすると,関数 f[vlist,m]が作成された各シンプレックスに適用される.ただし,vlist は頂点のリストであり m は測度である,f[vlist,m]がTrueを返す場合は,シンプレックスがさらに分割される.
- AccuracyGoal->a でPrecisionGoal->p のとき,領域 reg あるいは離散化された領域 dreg とRegionSymmetricDifference[reg,dreg]中の任意の点との間の最大距離を
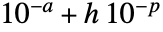 より小さく保とうと試みられる.ただし,
より小さく保とうと試みられる.ただし,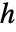 は境界ボックスの対角線の長さである.
は境界ボックスの対角線の長さである.

例題
すべて開く すべて閉じる例 (3)
スコープ (30)
1D領域 (5)
PointおよびLineは,1Dに存在可能な特殊領域である:
Line:
ImplicitRegionは,変数が1つだけなら,1Dである:
ParametricRegionは,関数を1つしか有していないのであれば,1Dである:
1DにおけるBooleanRegion:
2D領域 (8)
Point,Circle,Rectangleは,2Dに存在可能な特殊領域である:
Circleは1Dであるが,2Dに埋め込まれている:
Rectangleは2Dである:
ImplicitRegionは,変数が2つあれば,2Dである.1D領域は,方程式であることが多い:
ParametricRegionは,関数を2つ有するのであれば,2Dである.1D領域はパラメータを1つ持つ:
2つの厳密領域が与えられた場合は,ParametricRegionを使ってそのMinkowski和を表すことができる:
2DにおけるRegionUnion:
GeoGridPositionを使った多角形:
GeoPositionを使った多角形:
3D領域 (8)
Point,Line,Polygon,Ellipsoidは,3Dに存在可能な特殊領域である:
Line:
ImplicitRegionは,変数が3つであれば,3Dである.2D領域は方程式であることが多い:
3つの関数と3Dパラメータ空間を持つParametricRegionは3D立体である:
3つの関数と2Dパラメータ空間を持つParametricRegionは3Dに埋め込まれた曲面である:
球の下方表面に制限されたパラメータは2Dパラメータ空間にある:
3つの関数と1Dパラメータ空間を持つParametricRegionは3Dに埋め込まれた曲線である:
パラメータが混合次元領域にあるとき,そのパラメータは混合次元領域の一部でありうる:
パラメータが混合次元領域にあるところでParametricRegionを離散化する:
2つの厳密領域が与えられた場合は,ParametricRegionを使ってそれらのMinkowski和を表すことができる:
詳細 (2)
離散化におけるセルの測度はMaxCellMeasureを使って制御することができる:
デフォルトで,数として与えられた場合は埋込み次元に適用される:
非線形領域については,境界セルの測度はいくつかのオプションに依存する:
任意の線分の長さはMaxCellMeasureで制御できる:
曲線が視覚的に滑らかに見えるようにデフォルトのPrecisionGoalが値として選ばれる:
PrecisionGoal->Noneを使って境界測度をMaxCellMeasureに基づかせることができる:
AccuracyGoal->a を使って絶対許容度![]() を指定することができる:
を指定することができる:
品質 (7)
離散化におけるセルの測度はMaxCellMeasureを使って制御することができる:
MaxCellMeasureは低次元セルの大きさも制御できる:
離散化におけるセルの品質はMeshQualityGoalを使って制御することができる:
目標も"Minimal"あるいは"Maximal"に設定することができる:
MeshRefinementFunctionを使い,関数に基づいて離散化をさらに細かくできる:
細分化関数を加え,左上の象限における三角形をさらに小さくする:
AccuracyGoalを使い,離散化境界が厳密な境界に近いものであるようにする:
より高いAccuracyGoalを使った離散化は,真の境界により近い:
PrecisionGoalを使って離散化境界が厳密な境界に近いものであるようにする:
より高いPrecisionGoalを使った離散化は,真の境界により近い:
高品質の離散化については,PerformanceGoalを"Quality"に設定する:
オプション (28)
AccuracyGoal (1)
AccuracyGoalを使って離散化境界が厳密な境界に近いものであるようにする:
より高いAccuracyGoalを使った離散化は,真の境界により近い:
MaxCellMeasure (4)
MeshCellHighlight (3)
MeshCellHighlightを使うと,MeshRegionの一部のハイライトを設定することができる:
面を透明にすると,3D MeshRegionの内部構造を見ることができる:
MeshCellLabel (3)
MeshCellLabelを使ってMeshRegionの一部にラベルを付けることができる:
MeshCellMarker (1)
MeshCellMarkerを使ってMeshRegionの一部に値を割り当てることができる:
MeshCellLabelを使ってマーカーを示す:
MeshCellShapeFunction (2)
MeshCellStyle (3)
MeshCellStyleを使うとMeshRegionの一部のスタイルを指定することができる:
面を透明にすると,3D MeshRegionの内部構造を見ることができる:
Method (6)
"Continuation"法は,コーナー,尖端,急激な変化を多くの場合にきわめてうまく結合する曲線連続法を使う:
"RegionPlot"法はRegionPlotからの出力を向上させることに基づいており,より速いこともある:
"DiscretizeGraphics"法はグラフィックスプリミティブに最適化されている:
3D領域についての"RegionPlot3D"法はRegionPlot3Dに基づいている:
3D領域の"ContourPlot3D"法はContourPlot3Dに基づいている:
PrecisionGoal (1)
PrecisionGoalを使って離散化境界が厳密な境界に近いものであるようにする:
より高いPrecisionGoalを使った離散化は,真の境界により近い:
アプリケーション (2)
特性と関係 (5)
DiscretizeRegionの出力はMeshRegionである:
TriangulateMeshを使ってMeshRegionを再度離散化することができる:
しかし,もとの領域だけを離散化した方が,境界をより正確に離散化することができる:
DiscretizeRegionは,MeshRegionに適用されるとTriangulateMeshに等しい:
DiscretizeRegionは,穴のある領域を離散化することができる:
DiscretizeRegionは,不連続な成分がある領域を離散化することができる:
関連するガイド
-
▪
- メッシュベースの幾何学的領域 ▪
- 幾何学的計算
テキスト
Wolfram Research (2014), DiscretizeRegion, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscretizeRegion.html (2015年に更新).
CMS
Wolfram Language. 2014. "DiscretizeRegion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/DiscretizeRegion.html.
APA
Wolfram Language. (2014). DiscretizeRegion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscretizeRegion.html
BibTeX
@misc{reference.wolfram_2025_discretizeregion, author="Wolfram Research", title="{DiscretizeRegion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/DiscretizeRegion.html}", note=[Accessed: 06-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretizeregion, organization={Wolfram Research}, title={DiscretizeRegion}, year={2015}, url={https://reference.wolfram.com/language/ref/DiscretizeRegion.html}, note=[Accessed: 06-February-2026]}