Expectation
Expectation[expr,xdist]
x が確率分布 dist に従うという仮定の下で expr の期待値を与える.
Expectation[expr,xdata]
x が data によって与えられた確率分布に従うという仮定の下での expr の期待値を与える.
Expectation[expr,{x1,x2,…}dist]
{x1,x2,…}が多変量分布 dist に従うという仮定の下で expr の期待値を与える.
Expectation[expr,{x1dist1,x2dist2,…}]
x1, x2, …が独立であり分布 dist1, dist2, …に従うという仮定の下で expr の期待値を与える.
Expectation[exprpred,…]
pred を仮定して expr の条件付き期待値を与える.
詳細とオプション

- Expectationは期待値としても知られている.
- xdist は x
 dist
dist dist または x \[Distributed]dist と入力できる.
dist または x \[Distributed]dist と入力できる. - exprpred は expr
 cond
cond pred または expr \[Conditioned]pred と入力できる.
pred または expr \[Conditioned]pred と入力できる. - 連続分布 dist では,expr の期待値は
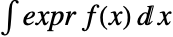 で与えられる.ただし,
で与えられる.ただし,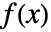 は dist の確率密度関数であり,積分は dist の領域で行われるものとする.
は dist の確率密度関数であり,積分は dist の領域で行われるものとする. - 離散分布 dist では,expr の期待値は
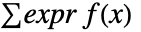 で与えられる.ただし,
で与えられる.ただし,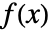 は dist の確率密度関数であり,総和は dist の領域で行われるものとする.
は dist の確率密度関数であり,総和は dist の領域で行われるものとする. - データ集合 data では,expr の期待値はSum[expr,{x,data}]/Length[data]で与えられる.
- 一変量データは値のリスト{v1,v2,…}として,多変量データはベクトルのリスト{{v11,…,v1m},{v21,…,v2m},…}として与えられる.
- Expectation[expr,{x1dist1,x2dist2}]はExpectation[Expectation[expr,x2dist2],x1dist1]に対応するので,最後の変数が最初に総和を求められたり積分されたりする.
- N[Expectation[…]]は記号的に求まらない期待値についてはNExpectationを呼び出す. »
- 使用可能なオプション
-
Assumptions $Assumptions 母数についての仮定 » GenerateConditions False 母数についての条件を生成するかどうか Method Automatic 使用するメソッド » TargetUnits Automatic 出力で表示する単位 »
予備知識
- Expectation[expr,x]は,確率変数 x を含む式 expr の,x が指示された確率分布に従う(つまり, はNormalDistribution,BinomialDistribution,ChiSquareDistribution等のような分布である)か,あるいは指定されたデータ集合から取られた(つまり, がデータ集合を定義する)場合の期待値を与える. はDistributedの短縮表現である.Expectationの出力は,数値あるいは入力パラメータを含む記号式であることがある.
- Expectationは,多変量分布にも,EmpiricalDistribution,HistogramDistribution,KernelMixtureDistributionのようなノンパラメトリック多変量分布にも,TransformedDistributionやProductDistribution等の派生分布に使うこともできる.Expectationは,ContinuousMarkovProcess,DiscreteMarkovProcess,WienerProcess,PoissonProcess等で定義されるものを含むランダム過程に使うこともできる.
- Expectationに渡された式は,線形および非線形の式や実数および複素数の変数を持つ関数を含むことがある.Expectationは,exprpred という形を使って条件付きの期待値を計算することができる. はConditionedをの短縮表現である.Assumptions,GenerateConditions,Methodを含む多くのオプションをExpectationに渡すことができる.Expectationの出力は,記号積分や総和を含む厳密メソッドで計算される.これに対応する数値メソッドを含む結果はNExpectationで得ることができる.
- 定義上,分布 に従って分布している確率変数 x の期待値Expectation[x,x]は,第1モーメントMoment[,1]に等しく,したがって平均Mean[]とも等しい.加えて,ExpectationとBoole構造をペアにすると,Expectationから得た結果がProbability.からも得られるようになる.例えば,Expectation[Boole[1<x<3],xNormalDistribution[]]はProbability[1<x<3, xNormalDistribution[]]と等しいのである.
例題
すべて開くすべて閉じるスコープ (31)
基本的な用法 (9)
記号評価が失敗した場合はN[Expectation[…]]を適用してNExpectationを呼び出す:
Assumptionsがない場合は,条件が生成される:
Assumptionsがある場合は,指定された仮定の下で有効な結果が返される:
数量の使用 (5)
QuantityDistributionを使って指定された期待値を求める:
QuantityMagnitudeで期待値を計算する:
Quantityデータで与えられる分布で期待値を計算する:
QuantityArrayで与えられる分布:
ノンパラメトリック分布 (4)
一変量のEmpiricalDistributionを使って期待値を計算する:
一変量のHistogramDistributionを使う:
一変量のKernelMixtureDistributionを使う:
打切りデータをSurvivalDistributionと一緒に使う:
派生分布 (9)
TransformedDistributionを使って期待値を計算する:
ProductDistributionを使って期待値を求める:
オプション (6)
Assumptions (1)
Assumptionsがない場合は条件が生成される:
Assumptionsがある場合は,指定された仮定の下で有効な結果が返される:
Method (4)
Expectationの定義を積分として使うと評価が遅くなる:
ここでは,式が多項式ではないのでモーメントに基づくメソッドはうまくいかない:
Expectationの定義を記号和として使うと結果が得られる:
TukeyLambdaDistribution中の関数の期待値を求める:
Quantileを使うと期待値を計算することができる:
この例ではIntegrateを使う:
Activateを使って結果を評価する:
TargetUnits (1)
アプリケーション (20)
分布特性 (5)
ParameterMixtureDistributionを使って同じ結果を直接得る:
保険数理 (5)
ある保険会社の契約では10を上限として損失を払い戻すことになっている.契約者の損失 ![]() は
は ![]() では密度関数
では密度関数![]() に従いその他の場合は0である.保険契約下で支払われる給付金の期待値を求める:
に従いその他の場合は0である.保険契約下で支払われる給付金の期待値を求める:
ある保険会社では月ごとの保険金支払い請求は,その確率密度関数が![]() で
で![]() に比例する正の連続確率変数
に比例する正の連続確率変数 ![]() でモデル化できる.この会社の月ごとの請求の期待値を求める:
でモデル化できる.この会社の月ごとの請求の期待値を求める:
風害を被った被保険家屋に対しての保険金支払い請求は,![]() については共通密度関数
については共通密度関数![]() の独立確率変数で,その他の場合は0である.
の独立確率変数で,その他の場合は0である.![]() は千を単位とした請求額である.このような請求が3件あったとする.この3件のうち請求額が最も大きいものの期待値を求める:
は千を単位とした請求額である.このような請求が3件あったとする.この3件のうち請求額が最も大きいものの期待値を求める:
![]() は保険に加入していて事故に遭った車両の年齢を表しているとする.
は保険に加入していて事故に遭った車両の年齢を表しているとする.![]() は事故時点で当該車両の持ち主が保険に加入していた期間を表す.
は事故時点で当該車両の持ち主が保険に加入していた期間を表す.![]() と
と ![]() の複合確率密度関数は
の複合確率密度関数は![]() と
と![]() については
については![]() で,その他の場合は0である.保険に加入していた車両の事故にあった時点での車齢の期待値を求める:
で,その他の場合は0である.保険に加入していた車両の事故にあった時点での車齢の期待値を求める:
損害額再保険契約の超過があると,請求が保有レベルと呼ばれる固定額を超過した場合にのみ,保険会社と再保険会社がその請求額の支払い責任をともに負う.それ以外の場合は保険会社が請求額を満額支払う.請求額が母数 ![]() と
と ![]() の対数正規分布に従うとして保有レベル
の対数正規分布に従うとして保有レベル ![]() の場合に保険会社と再保険会社がそれぞれ支払う額
の場合に保険会社と再保険会社がそれぞれ支払う額 ![]() と
と ![]() の期待値を計算する.保険会社が請求に対して支払う期待値を求める:
の期待値を計算する.保険会社が請求に対して支払う期待値を求める:
金融 (2)
時間 ![]() に支払われる1ドルの死亡手当の期待される時間的価値を計算する.
に支払われる1ドルの死亡手当の期待される時間的価値を計算する.![]() はGompertz–Makeham分布から導かれるものとする:
はGompertz–Makeham分布から導かれるものとする:
通常保険年の年初めに支払われ,![]() 期間における支払いの期待される時間的価値が1回の正味の保険料と等しくなるために必要である,年間保険料を求める(
期間における支払いの期待される時間的価値が1回の正味の保険料と等しくなるために必要である,年間保険料を求める(![]() はGompertz–Makeham分布から導かれるものとする):
はGompertz–Makeham分布から導かれるものとする):
株価の時間 ![]() (単位:年)における変動の割合
(単位:年)における変動の割合 ![]() は,母数
は,母数 ![]() と
と ![]() の対数正規分布に従うと考えられている:
の対数正規分布に従うと考えられている:
投資家が1年間年利率 ![]() で連続複利計算して無リスクで投資できる,配当が年間
で連続複利計算して無リスクで投資できる,配当が年間 ![]() である株に投資するとすると,リスク中立の価格条件には以下が必要である:
である株に投資するとすると,リスク中立の価格条件には以下が必要である:
この株を固定価格 ![]() で今から1年後に買うオプションを考える.このようなコールオプションの値は次のようになる:
で今から1年後に買うオプションを考える.このようなコールオプションの値は次のようになる:
同様に,今から1年後に固定価格 ![]() でこの株を売るためのプットオプションについて考える.そのようなオプションの値は次のようになる:
でこの株を売るためのプットオプションについて考える.そのようなオプションの値は次のようになる:
コールオプションおよびプットオプションのリスク中立価格はオプションの期待値の現行値として決まる:
これで,![]() である著名なプットコールパリティの関係を確立することができる:
である著名なプットコールパリティの関係を確立することができる:
利率 ![]() が5%,2%の配当,変動母数
が5%,2%の配当,変動母数 ![]() が0.087,株式の初期値が1株あたり200ドル,行使価格が1株あたり190ドルとすると,ブラック・ショールズのコールオプションおよびプットオプションの価格は次のようになる:
が0.087,株式の初期値が1株あたり200ドル,行使価格が1株あたり190ドルとすると,ブラック・ショールズのコールオプションおよびプットオプションの価格は次のようになる:
上記の結果は,FinancialDerivativeとうまく比較することができる:
ランダムな実験 (2)
連続分布 ![]() からのサイズ10のランダムサンプルが昇順に並べられている.新たな確率変量が生成される.11番目のサンプルが,ソートされたリストの小さい方から4番目と5番目の間に位置する確率を求める:
からのサイズ10のランダムサンプルが昇順に並べられている.新たな確率変量が生成される.11番目のサンプルが,ソートされたリストの小さい方から4番目と5番目の間に位置する確率を求める:
最大値3つの和の期待値を求める.恒等式 ![]() とExpectationの線形性を使うと以下が得られる:
とExpectationの線形性を使うと以下が得られる:
特性と関係 (10)
NExpectationを使って期待値を数値で求める:
Expectationを使って同じ結果を得る:
記号計算が失敗した場合,N[Expectation[…]]はNExpectationに等しい:
AsymptoticExpectationを使って期待値の漸近近似を求める:
Asymptotic[Expectation[…]]を使って同じ結果を得る:
Mean,Moment, Variance,その他の特性は期待値として定義される:
MomentGeneratingFunctionを含む母関数は期待値で定義される:
リストで指定される分布に関しては,ExpectationはMeanを使うことに等しい:
考えられる問題 (1)
デフォルトで,IntegrateのGenerateConditionsがFalseに設定されているため,Expectationが正しくない結果を与えることがある:
GenerateConditionsをTrueに設定して結果が正しくなるようにする:
テキスト
Wolfram Research (2010), Expectation, Wolfram言語関数, https://reference.wolfram.com/language/ref/Expectation.html (2016年に更新).
CMS
Wolfram Language. 2010. "Expectation." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/Expectation.html.
APA
Wolfram Language. (2010). Expectation. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Expectation.html