FRatioDistribution

FRatioDistribution[n,m]

分子の自由度 n，分母の自由度 m のF分布を表す．

詳細

  • FRatioDistributionはFisher–Snedecor分布としても知られている．
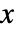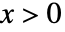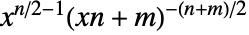  • F分布における値 の確率密度は，のときは に比例し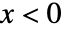，のときは0である． »
  • 整数 n と m について，F分布は正規分布から取ったサンプルの分散の割合の分布を与える．
  • FRatioDistributionでは，n と m は任意の正の実数でよい．
  • FRatioDistributionでは，n と m は無次元量でよい． »
  • FRatioDistributionは，Mean，CDF，RandomVariate等の関数で使うことができる． »

予備知識

  • FRatioDistribution[n,m]は，区間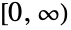上で比 X=Y1/Y2の分布として定義される連続統計分布を表す．ただし，Y1ChiSquareDistribution[n]およびY2ChiSquareDistribution[m]は自由度がそれぞれ n および m の独立変量である．確率密度関数(PDF)は，n および m の値によって，単峰性，あるいは潜在的特異値がその領域の下限に近付く単調減少となる．加えて，PDFの裾部はPDFが 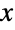の大きい値について指数的というよりも代数的に減少するという意味で「太い」（この動作は，分布のSurvivalFunctionを分析することによって数量的に厳密にできる）．F分布はFisher–Snedecor分布，（中央）F分布，SnedecoのF分布と呼ばれることもある．
  • F分布は，英国人の統計学者であるR. A. Fisherが1910年代の終りに導入した分散分析を向上させるためのツールとして，1930年代の中頃にアメリカ人の数学者であるG. W. Snedecorによって初めて形式化された．F分布は，近代統計学にとって必須であり，いわゆるF検定の基礎をなしている．F検定は，F分布に従う検定統計が帰無仮説に含まれた検定である．これは，よく使われる数多くの仮説を検定するために使われる．例として，提案された回帰モデルがある種のデータ集合にフィットしているか，あるいは標準偏差が等しい正規分布に従う母集団の平均は等しいか，等が挙げられる．このような検定の普遍性のために，F分布は，経済学，心理学，薬学，工学，医学，製造業を含む数多くの分野で使われている．
  • RandomVariateを使って，F分布から，1つあるいは複数の機械精度あるいは任意精度（後者はWorkingPrecisionオプションを介す）の擬似乱数変量を得ることができる．Distributed[x,FRatioDistribution[n,m]]（より簡略すると xFRatioDistribution[n,m]）を使って，確率変数 x が，F分布に従って分布していると宣言することができる．このような宣言は，Probability，NProbability，Expectation，NExpectation等の関数で使うことができる．
  • 確率密度関数および累積分布関数は，PDF[FRatioDistribution[n,m],x]およびCDF[FRatioDistribution[n,m],x]を使って得られることがある．平均，中央値，分散，原点の周りのモーメント，中心モーメントは，それぞれMean，Median，Variance，Moment，CentralMomentを使って計算することができる．
  • DistributionFitTestを使って，与えられたデータ集合がF分布と一致するかどうかを検定することが，EstimatedDistributionを使って与えられたデータからパラメトリックF分布を推定することが，FindDistributionParametersを使ってデータをF分布にフィットすることができる．ProbabilityPlotを使って記号F分布のCDFに対する与えられたデータのCDFのプロットを生成することが，QuantilePlotを使って記号F分布の変位値に対する与えられたデータの変位値のプロットを生成することができる．
  • TransformedDistributionを使って変換されたF分布を表すことが，CensoredDistributionを使って上限値と下限値の間で切り取られた値の分布を表すことが，TruncatedDistributionを使って上限値と下限値の間で切断された値の分布を表すことができる．CopulaDistributionを使ってF分布を含む高次元分布を構築することが，ProductDistributionを使ってF分布含む独立成分分布の結合分布を計算することができる．
  • F分布は他の数多くの分布に関係している．特に，先述したように，FRatioDistributionはChiSquareDistributionによって定義される（したがって ChiDistributionと関連がある）．さらに，FRatioDistribution[1,m]のPDFは，m がInfinityに近付くにしたがって，ChiSquareDistribution[1]のPDFに近付く．FRatioDistributionは単純な変換すなわちStudentTDistributionの平方によって，あるいはLaplaceDistribution，FisherZDistribution等の分布のより複雑な変換によって，他の分布から得ることができる．FRatioDistributionは，FRatioDistribution[n,m]のPDFが厳密にNoncentralFRatioDistribution[n,m,0]とNoncentralFRatioDistribution[n,m,0,0]の両方のPDFであるという意味で，NoncentralFRatioDistributionの特殊ケースであり，BetaDistribution，PearsonDistribution，HotellingTSquareDistribution，BinomialDistributionとも関係がある．

例題

すべて開くすべて閉じる

例  (4)

確率密度分数：

累積分布関数：

平均と分散：

中央値：

スコープ  (8)

F分布から擬似乱数のサンプルを生成する：

このヒストグラムを確率密度関数と比較する：

分布母数推定：

サンプルデータから分布母数を推定する：

サンプルの密度ヒストグラムを推定分布の確率密度関数と比較する：

歪度は自由度とともに変化する：

極限値：

尖度は自由度とともに変化する：

極限値はNormalDistributionの尖度である：

母数の関数としての閉形式の種々のモーメント：

Moment：

記号次数の閉形式：

CentralMoment：

FactorialMoment：

Cumulant：

ハザード関数：

分位関数：

次元Quantityを使って自由度母数 n と m を指定する：

アプリケーション  (1)

FRatioDistributionは2つの正規分布から取られた2つのサンプル分散の比の分布である．フィッシャー(Fisher)統計を定義する：

2つの標準正規分布から1000バッチのサンプルを生成する：

各バッチについてフィッシャー統計の値を計算する：

最初のバッチのフィッシャー検定の 値を求める：

FisherRatioTestと比較する：

特性と関係  (13)

FRatioDistributionは逆数の下では閉じている：

他の分布との関係：

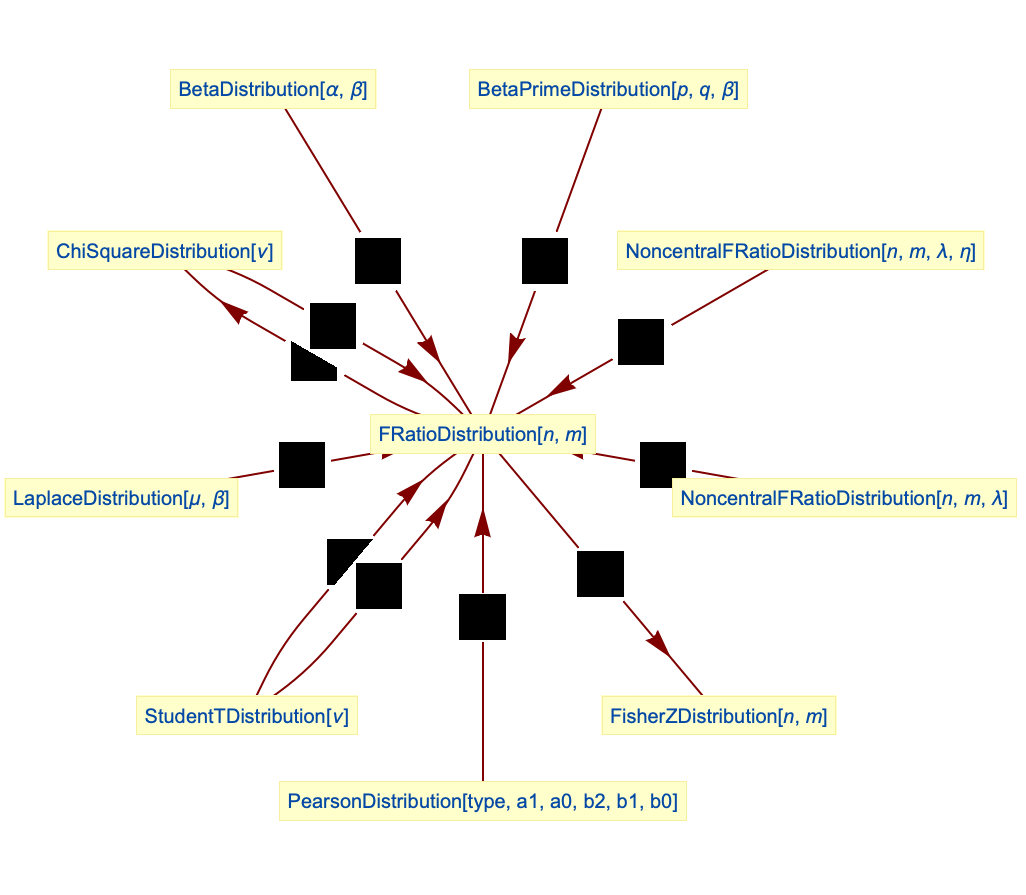
ChiSquareDistributionはF分布の極限の場合である：

F比は2つのChiSquareDistribution変数の比である：

F分布はBetaDistributionから得ることができる：

StudentTDistributionの二乗はF分布に従う：

F分布はStudentTDistributionの逆二乗分布である：

F分布はBetaPrimeDistributionの特殊ケースである：

F分布はタイプ6のPearsonDistributionの特殊ケースである：

FRatioDistributionはラプラス分布を変換したものである：

FisherZDistributionはF分布を変換したものである：

NoncentralFRatioDistributionを簡約するとF分布になる：

二重NoncentralFRatioDistributionを簡約するとF分布になる：

考えられる問題  (2)

FRatioDistributionは，n あるいは m が正の実数ではないときは定義されない：

記号出力に無効な母数値を代入すると意味のない結果となる：

おもしろい例題  (1)

累積分布関数の等高線を持つ n のさまざまな値についての確率密度関数：

Wolfram Research (2007), FRatioDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/FRatioDistribution.html （2016年に更新）.

テキスト

Wolfram Research (2007), FRatioDistribution, Wolfram言語関数， https://reference.wolfram.com/language/ref/FRatioDistribution.html （2016年に更新）.

CMS

Wolfram Language. 2007. "FRatioDistribution." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2016. https://reference.wolfram.com/language/ref/FRatioDistribution.html.

APA

Wolfram Language. (2007). FRatioDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FRatioDistribution.html

BibTeX

@misc{reference.wolfram_2024_fratiodistribution, author="Wolfram Research", title="{FRatioDistribution}", year="2016", howpublished="\url{https://reference.wolfram.com/language/ref/FRatioDistribution.html}", note=[Accessed: 25-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fratiodistribution, organization={Wolfram Research}, title={FRatioDistribution}, year={2016}, url={https://reference.wolfram.com/language/ref/FRatioDistribution.html}, note=[Accessed: 25-November-2024 ]}