GaussianOrthogonalMatrixDistribution[σ,n]
表示矩阵维度为 {n,n} 且尺度参数为 σ 的高斯正交矩阵分布.
GaussianOrthogonalMatrixDistribution[n]
表示带单位尺度参数的高斯正交矩阵分布.


GaussianOrthogonalMatrixDistribution
GaussianOrthogonalMatrixDistribution[σ,n]
表示矩阵维度为 {n,n} 且尺度参数为 σ 的高斯正交矩阵分布.
GaussianOrthogonalMatrixDistribution[n]
表示带单位尺度参数的高斯正交矩阵分布.
更多信息
- GaussianOrthogonalMatrixDistribution 也被称为高斯正交系综,或 GOE.
- GaussianOrthogonalMatrixDistribution 是对称矩阵
![(x+TemplateBox[{x}, Transpose])/2 (x+TemplateBox[{x}, Transpose])/2](Files/GaussianOrthogonalMatrixDistribution.zh/1.png) 的分布,其中
的分布,其中 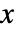 是由服从 NormalDistribution[0,σ] 分布的独立同分布矩阵元素组成的方阵.
是由服从 NormalDistribution[0,σ] 分布的独立同分布矩阵元素组成的方阵. - 矩阵
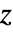 的概率密度正比于
的概率密度正比于 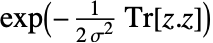 .
. - 尺度参数 σ 可以是任意正数,而 n 可以是任意正整数.
- GaussianOrthogonalMatrixDistribution 可以和诸如 MatrixPropertyDistribution,EstimatedDistribution 及 RandomVariate这样的函数一起使用.
背景
- GaussianOrthogonalMatrixDistribution[σ,n] 也称之为高斯正交系综 (GOE),表示在
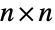 实对称矩阵上的统计分布,即满足
实对称矩阵上的统计分布,即满足 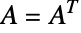 的方形实矩阵
的方形实矩阵 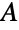 ,其中
,其中 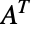 表示
表示 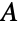 的转置. 按照 GaussianOrthogonalMatrixDistribution 分布的矩阵
的转置. 按照 GaussianOrthogonalMatrixDistribution 分布的矩阵 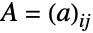 具有与
具有与 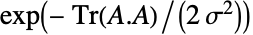 成正比的概率密度. 此外,所有项的
成正比的概率密度. 此外,所有项的 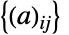 集合是按 NormalDistribution[0,σ] 同分布的实变量的独立集合. GaussianOrthogonalMatrixDistribution[σ,n] 由正整数 n(维数参数)和正实数 σ(标量参数)参数化. 尽管名字是“高斯正交矩阵分布”,但是属于该分布的矩阵不需要是正交的.
集合是按 NormalDistribution[0,σ] 同分布的实变量的独立集合. GaussianOrthogonalMatrixDistribution[σ,n] 由正整数 n(维数参数)和正实数 σ(标量参数)参数化. 尽管名字是“高斯正交矩阵分布”,但是属于该分布的矩阵不需要是正交的. - 一个参数形式的 GaussianOrthogonalMatrixDistribution[n] 等价于 GaussianOrthogonalMatrixDistribution[1,n].
- 与高斯辛分布和高斯酉分布(分别为 GaussianSymplecticMatrixDistribution 和 GaussianUnitaryMatrixDistribution)一起,高斯正交矩阵分布是 3 个高斯矩阵系综之一,最初是由 Eugene Wigner 建议为核物理学中研究波动的工具. 数学上,GOE 通过正交矩阵的共轭是不变的,其物理性模拟了带有时间反演对称性的哈密顿体系. 矩阵系综,像高斯正交矩阵分布在学习随机矩阵理论,以及物理和数学的各种分支中是相当的重要.
- RandomVariate 可用于从高斯正交矩阵分布中给出一个或多个机器或随机精度(后者是通过 WorkingPrecision 选项)的伪随机变数,这种变数集合的均值、中位数、方差、原始矩和中心矩可分别用 Mean、Median、Variance、Moment 和 CentralMoment 进行计算. Distributed[A,GaussianOrthogonalMatrixDistribution[σ,n]] 可以更简明地写成 AGaussianOrthogonalMatrixDistribution[σ,n],可用于断言随机矩阵 A 是按高斯正交矩阵分布分布的. 这种断言可用于函数,诸如 MatrixPropertyDistribution.
- 按照高斯正交矩阵分布的变数的轨迹、特征值和范数可以分别用 Tr、Eigenvalues 和 Norm 计算. 这种变数也可以用 MatrixFunction 和 MatrixPower 进行检验,这种变数的项可以用 MatrixPlot 进行绘制.
- GaussianOrthogonalMatrixDistribution 也与其他分布相关. 如上所讨论,定性地讲,它类似于GaussianSymplecticMatrixDistribution 和 GaussianUnitaryMatrixDistribution. 高斯系综的泛化包括所谓的圆矩阵系综,因此 GaussianOrthogonalMatrixDistribution 也与 CircularOrthogonalMatrixDistribution、CircularQuaternionMatrixDistribution、CircularRealMatrixDistribution、CircularSymplecticMatrixDistribution 和 CircularUnitaryMatrixDistribution 相关. GaussianOrthogonalMatrixDistribution 也与 MatrixNormalDistribution、MatrixTDistribution、WishartMatrixDistribution、InverseWishartMatrixDistribution、TracyWidomDistribution 和 WignerSemicircleDistribution 相关.
范例
打开所有单元 关闭所有单元基本范例 (4)
从 GaussianOrthogonalMatrixDistribution 得到的矩阵项是联合高斯分布且不相关,不在对角线上的项的方差是对角线上项的方差的一半:
使用 MatrixPropertyDistribution 对 GOE 矩阵的特征值采样:
范围 (4)
应用 (3)
比较直方图和解析形式,其中解析形式也被称为 Dyson 指数 ![]() 的 Wigner 估测:
的 Wigner 估测:
使用 RandomSample 随机排列特征值以补偿因算法指定的顺序:
属性和关系 (4)
MatrixExp 作用于 ![]() 而
而 ![]() 采样于 GaussianOrthogonalMatrixDistribution,结果既是对称矩阵也是酉矩阵:
采样于 GaussianOrthogonalMatrixDistribution,结果既是对称矩阵也是酉矩阵:
GOE 矩阵的上三角部分的矩阵元素是独立的高斯分布随机变量:
使用 IndependenceTest 验证独立性:
大型 GOE 矩阵的谱密度收敛到 WignerSemicircleDistribution:
大型 GOE 矩阵的缩放的最大特征值的分布收敛于 TracyWidomDistribution:
文本
Wolfram Research (2015),GaussianOrthogonalMatrixDistribution,Wolfram 语言函数,https://reference.wolfram.com/language/ref/GaussianOrthogonalMatrixDistribution.html (更新于 2017 年).
CMS
Wolfram 语言. 2015. "GaussianOrthogonalMatrixDistribution." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2017. https://reference.wolfram.com/language/ref/GaussianOrthogonalMatrixDistribution.html.
APA
Wolfram 语言. (2015). GaussianOrthogonalMatrixDistribution. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/GaussianOrthogonalMatrixDistribution.html 年
BibTeX
@misc{reference.wolfram_2025_gaussianorthogonalmatrixdistribution, author="Wolfram Research", title="{GaussianOrthogonalMatrixDistribution}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/GaussianOrthogonalMatrixDistribution.html}", note=[Accessed: 12-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_gaussianorthogonalmatrixdistribution, organization={Wolfram Research}, title={GaussianOrthogonalMatrixDistribution}, year={2017}, url={https://reference.wolfram.com/language/ref/GaussianOrthogonalMatrixDistribution.html}, note=[Accessed: 12-January-2026]}