Hexahedron
✖
Hexahedron
詳細とオプション

- Hexahedronは,幾何領域としてあるいはグラフィックスプリミティブとして使うことができる.
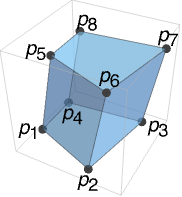
- Hexahedronは,{p4,p3,p2,p1},{p1,p2,p6,p5},{p2,p3,p7,p6},{p3,p4,p8,p7},{p4,p1,p5,p8},{p5,p6,p7,p8}の多角形面で与えられる塗り潰された多面体を表す.
- CanonicalizePolyhedronを使って六面体を明示的なPolyhedronオブジェクトに変換できる.
- Hexahedronは,Graphics3Dで使える.
- グラフィックスでは,点 pi は,ScaledおよびDynamicの式になり得る.
- グラフィックスの描画は,FaceForm,EdgeForm,Opacity,Texture,色等の指示子に影響される.
- グラフィックスで使える設定とオプション
-
VertexColors Automatic 補間される頂点の色 VertexNormals Automatic 陰影のための有効な頂点の法線 VertexTextureCoordinates None テクスチャのための座標
例題
すべて開くすべて閉じる例 (3)基本的な使用例
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-f8gaof
Out[1]=1
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-sxptmj
In[2]:=2

✖
https://wolfram.com/xid/0tqnzefqf8y3zm-84fmk
Out[2]=2
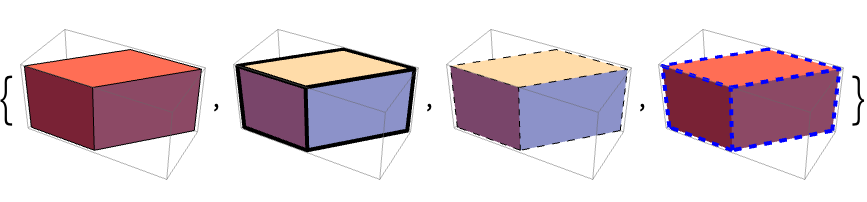
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-zpy9vm
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-kgn009
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-hd55qh
Out[3]=3
スコープ (18)標準的な使用例のスコープの概要
グラフィックス (8)
指定 (2)
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-ce4k03
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-ggb1ww
Out[2]=2
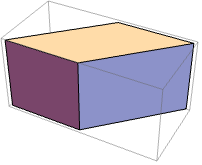
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-1c6641
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-h7cw3f
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-ppozsb
Out[3]=3
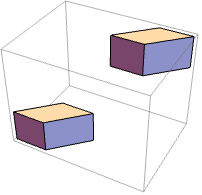
スタイリング (3)
FaceFormとEdgeFormを使って,面と辺のスタイルを指定することができる:
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-38df6s
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-78t7nc
Out[2]=2
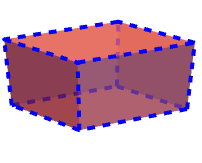
Textureを面に適用する:
In[1]:=1
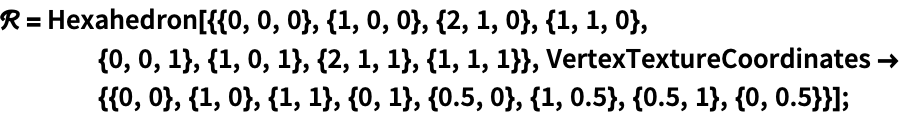
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-vff8kd
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-5tt6t
Out[2]=2

VertexColorsを頂点に割り当てる:
In[1]:=1

✖
https://wolfram.com/xid/0tqnzefqf8y3zm-2h0wgx
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-twbbe6
Out[2]=2
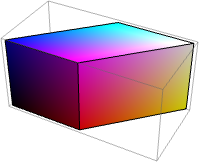
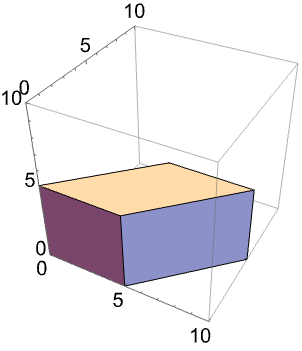
座標 (3)
In[1]:=1

✖
https://wolfram.com/xid/0tqnzefqf8y3zm-prz04t
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-u8d4ip
Out[2]=2
In[1]:=1

✖
https://wolfram.com/xid/0tqnzefqf8y3zm-po136z
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-6qq3xm
Out[2]=2
点はDynamicでもよい:
In[1]:=1
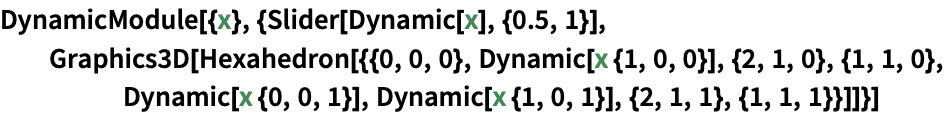
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-3sh852
Out[1]=1

領域 (10)
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-e3gvsm
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-y220
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-bx9tom
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-j5s1r5
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-p89qc
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-d9nxgd
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-se0twe
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-e06l44
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-gwq4b4
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-oknxhk
Out[4]=4
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-i8cqms
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-bruj1e
Out[2]=2
In[3]:=3

✖
https://wolfram.com/xid/0tqnzefqf8y3zm-jdsxbg
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-h7eno
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-b7y6q0
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-6fqw5x
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-et4yza
Out[2]=2
In[3]:=3

✖
https://wolfram.com/xid/0tqnzefqf8y3zm-e29k5d
In[4]:=4
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-5ksoo8
In[5]:=5

✖
https://wolfram.com/xid/0tqnzefqf8y3zm-g70sch
Out[5]=5
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-yw9mlv
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-wv3700
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-p10u0d
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-h2d2dj
Out[4]=4
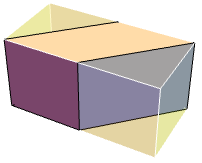
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-c81tiw
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-banwkr
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-fdvdlz
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-hyz4dq
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-hzsonx
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-cn6ygq
Out[2]=2
アプリケーション (4)この関数で解くことのできる問題の例
CuboidをHexahedronに変換する:
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-4oja0n
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-0walhg
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-k2amp6
Out[3]=3
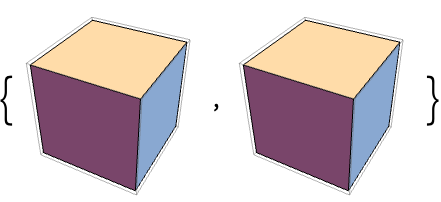
ParallelepipedをHexahedronに変換する:
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-yhh4gh
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-swkgj9
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-lexi2a
Out[3]=3
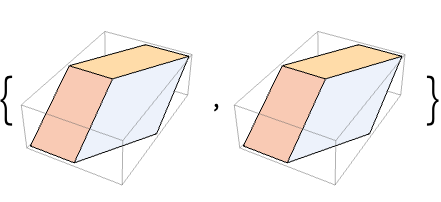
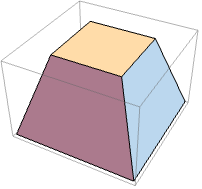
底の幅,最上部の幅,および高さでパラメータ化された正方形の錐台を作る:
In[1]:=1

✖
https://wolfram.com/xid/0tqnzefqf8y3zm-fezsch
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-mc91r4
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-qxe5bt
Out[3]=3
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-1ykska
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-o8u6ym
Out[2]=2
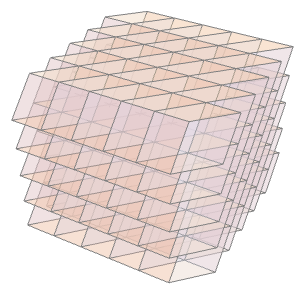
特性と関係 (4)この関数の特性および他の関数との関係
Hexahedronは次元3で,Cuboidを一般化したものである:
In[1]:=1
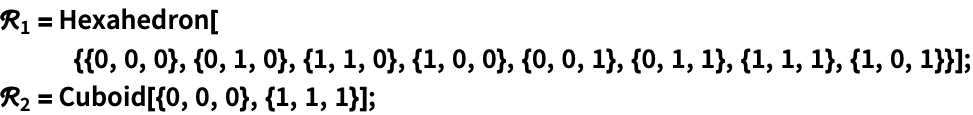
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-c1q2ki
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-0uif6
Out[2]=2
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-u32usv
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-h426c
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-mtv2bj
In[4]:=4
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-sos1yg
Out[4]=4
In[1]:=1
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-jufwh0
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-ehckv7
In[3]:=3
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-cc9t05
Out[3]=3
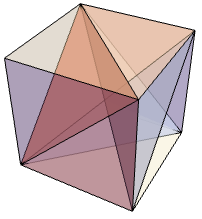
ImplicitRegionは,任意のHexahedronを表すことができる:
In[1]:=1
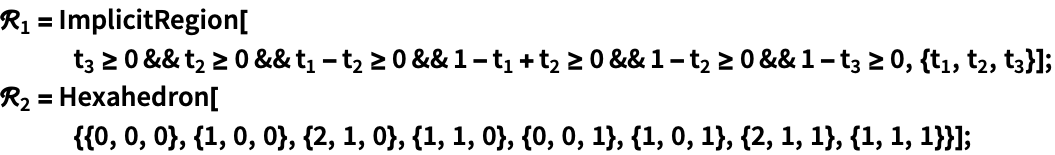
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-hw5ae3
In[2]:=2
✖
https://wolfram.com/xid/0tqnzefqf8y3zm-jmnohi
Out[2]=2
Wolfram Research (2014), Hexahedron, Wolfram言語関数, https://reference.wolfram.com/language/ref/Hexahedron.html (2019年に更新).
✖
Wolfram Research (2014), Hexahedron, Wolfram言語関数, https://reference.wolfram.com/language/ref/Hexahedron.html (2019年に更新).テキスト
Wolfram Research (2014), Hexahedron, Wolfram言語関数, https://reference.wolfram.com/language/ref/Hexahedron.html (2019年に更新).
✖
Wolfram Research (2014), Hexahedron, Wolfram言語関数, https://reference.wolfram.com/language/ref/Hexahedron.html (2019年に更新).CMS
Wolfram Language. 2014. "Hexahedron." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Hexahedron.html.
✖
Wolfram Language. 2014. "Hexahedron." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Hexahedron.html.APA
Wolfram Language. (2014). Hexahedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Hexahedron.html
✖
Wolfram Language. (2014). Hexahedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Hexahedron.htmlBibTeX
✖
@misc{reference.wolfram_2025_hexahedron, author="Wolfram Research", title="{Hexahedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Hexahedron.html}", note=[Accessed: 03-June-2025
]}BibLaTeX
✖
@online{reference.wolfram_2025_hexahedron, organization={Wolfram Research}, title={Hexahedron}, year={2019}, url={https://reference.wolfram.com/language/ref/Hexahedron.html}, note=[Accessed: 03-June-2025
]}